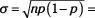Statistics Essentials For Dummies (16 page)

Because the
Z
-table only uses less-than probabilities, you have to rewrite all greater-than probabilities as "one minus" their corresponding less-than probabilities. That is, write everything in terms of percentiles.
Step 3: The 75th percentile of
Z
is the
z
-value where P(
Z
<
z
) = 0.75. Using the
Z
-table (Table A-1 in the appendix) you find the probability closest to 0.7500 is 0.7486, and its corresponding
z
-value is in the row for 0.6 and column for 0.07. Put these digits together and get a
z
-value of 0.67. This is the 75th percentile for
Z
. In Step 4, change the
z
-value back to an
x
-value (length in inches) using the
Z
-formula solved for
X
to get
x
= 16 + 0.67
*
4 = 18.68 inches. So, 25% of the fish are longer than 18.68 inches (answering the original question). And it's true, 75% of the fish are shorter than that.
Normal Approximation to the Binomial
Suppose you flip a fair coin 100 times, and you let
X
equal the number of heads. What's the probability that
X
is greater than 60? In Chapter 4, you solve problems like this using the binomial distribution. For binomial problems where
n
is small, you can either use the direct formula (found in Chapter 4) or the binomial table (Table A-3 in the appendix). However, when
n
is large, the calculations get unwieldy and the table runs out of numbers. What to do?
Turns out, if
n
is large enough, you can use the normal distribution to get an approximate answer that's very close to what you would get with the binomial distribution. To determine whether
n
is large enough to use the normal approximation, two (not just one) conditions must hold:
1. (
n
*
p) ≥ 10
2.
n
*
(1 -
p
) ≥ 10
In general, follow these steps to find the approximate probability for a binomial distribution when
n
is large:
1. Verify whether
n
is large enough to use the normal approximation by checking the two conditions.
For the coin-flipping question, the conditions are met since
n
*
p
= 100
*
0.50 = 50, and
n
*
(1 -
p
) = 100
*
(1 - 0.50) = 50, both of which are at least 10. So go ahead with the normal approximation.
2. Write down what you need to find as a probability statement about
X
.
For the coin-flipping example, find P(
X
> 60).
3. Transform the
x
-value to a
z
-value, using the
Z
-formula,.
For the mean of the normal distribution, use
=
n
*
p
(the mean of the binomial), and for the standard deviation, use
(the standard deviation of the binomial).
For the coin-flipping example, use
=
n
*
p
= 100
*
0.50 = 50 and
.
Now put these values into the
Z
-formula to get