Structure and Interpretation of Computer Programs (21 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

After debugging her program, Alyssa shows it to a potential user,
who complains that her program solves the wrong problem. He
wants a program that can deal with numbers represented as a center
value and an additive tolerance; for example, he wants to work with
intervals such as 3.5± 0.15 rather than [3.35, 3.65]. Alyssa
returns to her desk and fixes this problem by supplying an alternate
constructor and alternate selectors:
(define (make-center-width c w)
(make-interval (- c w) (+ c w)))
(define (center i)
(/ (+ (lower-bound i) (upper-bound i)) 2))
(define (width i)
(/ (- (upper-bound i) (lower-bound i)) 2))
Unfortunately, most of Alyssa's users are engineers. Real engineering
situations usually involve measurements with only a small uncertainty,
measured as the ratio of the width of the interval to the midpoint of
the interval. Engineers usually specify percentage tolerances on the
parameters of devices, as in the resistor specifications given
earlier.
Exercise 2.12.
Define a constructor
make-center-percent
that takes a center and
a percentage tolerance and produces the desired interval. You must
also define a selector
percent
that produces the
percentage tolerance for a given interval. The
center
selector
is the same as the one shown above.
Exercise 2.13.
Show that under the assumption of small percentage tolerances there is
a simple formula for the approximate percentage tolerance of the
product of two intervals in terms of the tolerances of the factors.
You may simplify the problem by assuming that all numbers are
positive.
After considerable work, Alyssa P. Hacker delivers her finished
system. Several years later, after she has forgotten all about it, she
gets a frenzied call from an irate user, Lem E. Tweakit.
It seems that Lem has
noticed that the formula for parallel resistors can be written in two
algebraically equivalent ways:
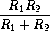
and
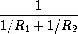
He has written the following two programs, each of which computes the
parallel-resistors formula differently:
(define (par1 r1 r2)
(div-interval (mul-interval r1 r2)
(add-interval r1 r2)))
(define (par2 r1 r2)
(let ((one (make-interval 1 1)))
(div-interval one
(add-interval (div-interval one r1)
(div-interval one r2)))))
Lem complains that Alyssa's program gives different answers for
the two ways of computing. This is a serious complaint.
Exercise 2.14.
Demonstrate that Lem is right. Investigate the behavior of the
system on a variety of arithmetic expressions. Make some intervals
A
and
B
,
and use them in computing the expressions
A
/
A
and
A
/
B
. You will
get the most insight by using intervals whose width is a small
percentage of the center value. Examine the results of the computation
in center-percent form (see exercise
2.12
).
Exercise 2.15.
Eva Lu Ator, another user, has also noticed the different intervals
computed by different but algebraically equivalent expressions. She
says that a formula to compute with intervals using Alyssa's system
will produce tighter error bounds if it can be written in such a form
that no variable that represents an uncertain number is repeated.
Thus, she says,
par2
is a “better” program for parallel
resistances than
par1
. Is she right? Why?
Exercise 2.16.
Explain, in general, why equivalent algebraic expressions may lead to
different answers. Can you devise an interval-arithmetic package that
does not have this shortcoming, or is this task impossible? (Warning:
This problem is very difficult.)
2
The name
cons
stands for “construct.” The
names
car
and
cdr
derive from the original implementation of
Lisp on the
IBM 704. That machine had an addressing scheme that
allowed one to reference the “address” and “decrement” parts of a
memory location.
Car
stands for “Contents of Address part of
Register” and
cdr
(pronounced “could-er”) stands for
“Contents of Decrement part of Register.”
3
Another way to define the selectors and constructor is
(define make-rat cons)
(define numer car)
(define denom cdr)
The first definition associates the name
make-rat
with the value of the expression
cons
, which is the primitive
procedure that constructs pairs. Thus
make-rat
and
cons
are names for the same primitive constructor.
Defining selectors and constructors in this way is efficient:
Instead of
make-rat
calling
cons
,
make-rat
is
cons
, so there is only one procedure called, not two,
when
make-rat
is called. On the other hand, doing this defeats debugging
aids that trace procedure calls or put breakpoints on procedure calls:
You may want to watch
make-rat
being called, but you certainly
don't want to watch every call to
cons
.
We have chosen not to use this style of definition in this book.
4
Display
is
the Scheme primitive for printing data. The Scheme primitive
newline
starts a new line for printing.
Neither of these procedures returns a useful value, so in the uses of
print-rat
below, we show only what
print-rat
prints,
not what the interpreter prints as the value returned by
print-rat
.
5
Surprisingly, this idea is very
difficult to formulate rigorously. There are two approaches to giving
such a formulation. One, pioneered by
C. A. R. Hoare (1972), is known
as the method of
abstract models
. It formalizes the
“procedures plus conditions” specification as outlined in the
rational-number example above. Note that the condition on the
rational-number representation was stated in terms of facts about
integers (equality and division). In general, abstract models define
new kinds of data objects in terms of previously defined types of data
objects. Assertions about data objects can therefore be checked by
reducing them to assertions about previously defined data objects.
Another approach, introduced by
Zilles at MIT, by
Goguen,
Thatcher,
Wagner, and
Wright at IBM (see Thatcher, Wagner, and Wright 1978), and by
Guttag at Toronto (see Guttag 1977),
is called
algebraic specification
. It regards the “procedures”
as elements of an abstract algebraic system whose behavior is
specified by axioms that correspond to our “conditions,” and uses
the techniques of abstract algebra to check assertions about data
objects. Both methods are surveyed in the paper by
Liskov and Zilles
(1975).
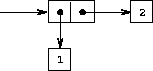
As we have seen, pairs provide a primitive “glue” that we can use to
construct compound data objects.
Figure
2.2
shows a standard way to
visualize a
pair – in this case, the pair formed by
(cons 1 2)
.
In this representation, which is called
box-and-pointer
notation
, each object is shown as a
pointer
to a box. The box
for a primitive object contains a representation of the object. For
example, the box for a number contains a numeral. The box for a pair
is actually a double box, the left part containing (a pointer to) the
car
of the pair and the right part containing the
cdr
.
We have already seen that
cons
can be used to combine not
only numbers but pairs as well. (You made use of this fact, or
should have, in doing exercises
2.2
and
2.3
.) As a consequence, pairs provide a universal
building block from which we can construct all sorts of data
structures. Figure
2.3
shows two ways
to use pairs to combine the numbers 1, 2, 3, and 4.
 |
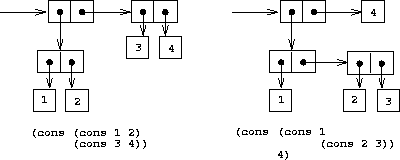 |
The ability to create pairs whose elements are pairs is the essence of
list structure's importance as a representational tool. We refer to
this ability as the
closure property
of
cons
. In general,
an operation for combining data objects satisfies the closure property
if the results of combining things with that operation can themselves
be combined using the same operation.
6
Closure is the key to power in
any means of combination because it permits us to create
hierarchical
structures – structures made up of parts, which
themselves are made up of parts, and so on.
From the outset of chapter 1, we've made essential use of closure in
dealing with procedures, because all but the very simplest programs
rely on the fact that the elements of a combination can themselves be
combinations. In this section, we take up the consequences of closure
for compound data. We describe some conventional techniques for using
pairs to represent sequences and trees, and we exhibit a graphics
language that illustrates closure in a vivid way.
7
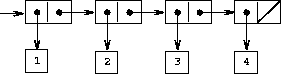 |