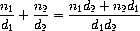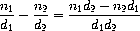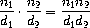Structure and Interpretation of Computer Programs (18 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

Consider the task of designing a system to perform arithmetic with
rational numbers. We could imagine an operation
add-rat
that takes
two rational numbers and produces their sum. In terms of
simple data, a rational number can be thought of as two integers: a
numerator and a denominator. Thus, we could design a program in which
each rational number would be represented by two integers (a numerator
and a denominator) and where
add-rat
would be implemented by two
procedures (one producing the numerator of the sum and one producing
the denominator). But this would be awkward, because we would then
need to explicitly keep track of which numerators corresponded to
which denominators. In a system intended to perform many operations
on many rational numbers, such bookkeeping details would clutter the
programs substantially, to say nothing of what they would do to our
minds. It would be much better if we could “glue together” a
numerator and denominator to form a pair – a
compound data
object
– that our programs could manipulate in a way that would be
consistent with regarding a rational number as a single conceptual
unit.
The use of compound data also enables us to increase the modularity of
our programs. If we can manipulate rational numbers directly as
objects in their own right, then we can separate the part of our
program that deals with rational numbers per se from the details of
how rational numbers may be represented as pairs of integers. The
general technique of isolating the parts of a program that deal with
how data objects are represented from the parts of a program that deal
with how data objects are used is a powerful design methodology called
data abstraction
. We will see how data abstraction makes
programs much easier to design, maintain, and modify.
The use of compound data leads to a real increase in the expressive
power of our programming language. Consider the idea of forming a
“linear combination”
a
x
+
b
y
. We might like to write a procedure
that would accept
a
,
b
,
x
, and
y
as arguments and return the
value of
a
x
+
b
y
. This presents no difficulty if the arguments are to
be numbers, because we can readily define the procedure
(define (linear-combination a b x y)
(+ (* a x) (* b y)))
But suppose we are not concerned only with numbers. Suppose we would
like to express, in procedural terms, the idea that one can form
linear combinations whenever addition and multiplication are
defined – for rational numbers, complex numbers, polynomials, or
whatever. We could express this as a procedure of the form
(define (linear-combination a b x y)
(add (mul a x) (mul b y)))
where
add
and
mul
are not the primitive procedures
+
and
*
but rather more complex things that will perform the
appropriate operations for whatever kinds of data we pass in as the
arguments
a
,
b
,
x
, and
y
. The key point is
that the only thing
linear-combination
should need to know about
a
,
b
,
x
, and
y
is that the procedures
add
and
mul
will perform the appropriate manipulations. From the
perspective of the procedure
linear-combination
, it is
irrelevant what
a
,
b
,
x
, and
y
are and even
more irrelevant how they might happen to be represented in terms of
more primitive data. This same example shows why it is important that
our programming language provide the ability to manipulate compound
objects directly: Without this, there is no way for a procedure such
as
linear-combination
to pass its arguments along to
add
and
mul
without having to know their detailed
structure.
1
We begin this chapter by implementing the rational-number arithmetic
system mentioned above. This will form the background for our
discussion of compound data and data abstraction. As with compound
procedures, the main issue to be addressed is that of abstraction as a
technique for coping with complexity, and we will see how data
abstraction enables us to erect suitable
abstraction barriers
between different parts of a program.
We will see that the key to forming compound data is that a
programming language should provide some kind of “glue” so that data
objects can be combined to form more complex data objects. There are
many possible kinds of glue. Indeed, we will discover how to form
compound data using no special “data” operations at all, only
procedures. This will further blur the distinction between
“procedure” and “data,” which was already becoming tenuous toward
the end of chapter 1. We will also explore some conventional
techniques for representing sequences and trees. One key idea in
dealing with compound data is the notion of
closure
– that the
glue we use for combining data objects should allow us to combine not
only primitive data objects, but compound data objects as well.
Another key idea is that compound data objects can serve as
conventional interfaces
for combining program modules in
mix-and-match ways. We illustrate some of these ideas by presenting a
simple graphics language that exploits closure.
We will then augment the representational power of our language by
introducing
symbolic expressions
– data whose elementary parts
can be arbitrary symbols rather than only numbers. We explore various
alternatives for representing sets of objects. We will find that,
just as a given numerical function can be computed by many different
computational processes, there are many ways in which a given data
structure can be represented in terms of simpler objects, and the
choice of representation can have significant impact on the time and
space requirements of processes that manipulate the data. We will
investigate these ideas in the context of symbolic differentiation,
the representation of sets, and the encoding of information.
Next we will take up the problem of working with data that may be
represented differently by different parts of a program. This leads
to the need to implement
generic operations
, which must handle
many different types of data. Maintaining modularity in the
presence of generic operations requires more powerful abstraction
barriers than can be erected with simple data abstraction alone. In
particular, we introduce
data-directed programming
as a
technique that allows individual data representations to be designed
in isolation and then combined
additively
(i.e., without
modification). To illustrate the power of this approach to system
design, we close the chapter by applying what we have learned to the
implementation of a package for performing symbolic arithmetic on
polynomials, in which the coefficients of the polynomials can be
integers, rational numbers, complex numbers, and even other
polynomials.
1
The ability to directly manipulate procedures
provides an analogous increase in the expressive power of a
programming language. For example, in
section
1.3.1
we introduced the
sum
procedure, which takes a procedure
term
as an argument and
computes the sum of the values of
term
over some specified
interval. In order to define
sum
, it is crucial that we be able
to speak of a procedure such as
term
as an entity in its own
right, without regard for how
term
might be expressed with more
primitive operations. Indeed, if we did not have the notion of “a
procedure,” it is doubtful that we would ever even think of the
possibility of defining an operation such as
sum
. Moreover,
insofar as performing the summation is concerned, the details of how
term
may be constructed from more primitive operations are
irrelevant.
In section
1.1.8
, we noted
that a procedure used as an element in creating a more complex
procedure could be regarded not only as a collection of particular
operations but also as a procedural abstraction. That is, the details
of how the procedure was implemented could be suppressed, and the
particular procedure itself could be replaced by any other procedure
with the same overall behavior. In other words, we could make an
abstraction that would separate the way the procedure would be used
from the details of how the procedure would be implemented in terms of
more primitive procedures. The analogous notion for compound data is
called
data abstraction
. Data abstraction is a methodology that
enables us to isolate how a compound data object is used from the
details of how it is constructed from more primitive data objects.
The basic idea of data abstraction is to structure the programs that
are to use compound data objects so that they operate on
“abstract
data.” That is, our programs should use data in such a way as to make
no assumptions about the data that are not strictly necessary for
performing the task at hand. At the same time, a
“concrete” data
representation is defined independent of the programs that use
the data. The interface between these two parts of our system will be
a set of procedures, called
selectors
and
constructors
,
that implement the abstract data in terms of the concrete
representation. To illustrate this technique, we will consider how to
design a set of procedures for manipulating rational numbers.
Suppose we want to do arithmetic with rational numbers. We want to be
able to add, subtract, multiply, and divide them and to test whether
two rational numbers are equal.
Let us begin by assuming that we already have a way of constructing a
rational number from a numerator and a denominator. We also assume
that, given a rational number, we have a way of extracting (or
selecting) its numerator and its denominator. Let us further assume
that the constructor and selectors are available as procedures:
- (make-rat <
n
> <
d
>)
returns the
rational number whose numerator is the integer
<
n
>
and whose denominator is the integer
<
d
>
. - (numer <
x
>)
returns the numerator of the rational
number
<
x
>
. - (denom <
x
>)
returns the denominator of the
rational number
<
x
>
.
We are using here a powerful strategy of synthesis:
wishful thinking
.
We haven't yet said how a rational number is represented, or how the
procedures
numer
,
denom
, and
make-rat
should be
implemented. Even so, if we did have these three procedures, we could
then add, subtract, multiply, divide, and test equality by using the
following relations: