Structure and Interpretation of Computer Programs (70 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

... John Barth, |
In our study of program design, we have seen that expert programmers
control the complexity of their designs with the same general
techniques used by designers of all complex systems. They combine
primitive elements to form compound objects, they abstract compound
objects to form higher-level building blocks, and they preserve
modularity by adopting appropriate large-scale views of system
structure. In illustrating these techniques, we have used Lisp as a
language for describing processes and for constructing computational
data objects and processes to model complex phenomena in the real
world. However, as we confront increasingly complex problems, we will
find that Lisp, or indeed any fixed programming language, is not
sufficient for our needs. We must constantly turn to new languages in
order to express our ideas more effectively. Establishing new
languages is a powerful strategy for controlling complexity in
engineering design; we can often enhance our ability to deal with a
complex problem by adopting a new language that enables us to describe
(and hence to think about) the problem in a different way, using
primitives, means of combination, and means of abstraction that are
particularly well suited to the problem at hand.
1
Programming is endowed with a multitude of languages. There are
physical languages, such as the machine languages for particular
computers. These languages are concerned with the representation of
data and control in terms of individual bits of storage and primitive
machine instructions. The machine-language programmer is concerned
with using the given hardware to erect systems and utilities for the
efficient implementation of resource-limited computations. High-level
languages, erected on a machine-language substrate, hide concerns
about the representation of data as collections of bits and the
representation of programs as sequences of primitive instructions.
These languages have means of combination and abstraction, such as
procedure definition, that are appropriate to the larger-scale
organization of systems.
Metalinguistic abstraction
– establishing new
languages – plays an important role in all branches of engineering
design. It is particularly important to computer programming, because
in programming not only can we formulate new languages but we can also
implement these languages by constructing evaluators. An
evaluator
(or
interpreter
) for a programming language is a procedure
that, when applied to an expression of the language, performs the
actions required to evaluate that expression.
It is no exaggeration to regard this as the most fundamental idea in
programming:
The evaluator, which determines the meaning of expressions in aTo appreciate this point is to change our images of ourselves as
programming language, is just another program.
programmers. We come to see ourselves as designers of languages,
rather than only users of languages designed by others.
In fact, we can regard almost any program as the evaluator for some
language. For instance, the polynomial manipulation system of
section
2.5.3
embodies the rules of polynomial
arithmetic and implements them in terms of operations on
list-structured data. If we augment this system with procedures to
read and print polynomial expressions, we have the core of a
special-purpose language for dealing with problems in symbolic
mathematics. The digital-logic simulator of
section
3.3.4
and the constraint propagator of
section
3.3.5
are legitimate languages in their own
right, each with its own primitives, means of combination, and means
of abstraction. Seen from this perspective, the technology for coping
with large-scale computer systems merges with the technology for
building new computer languages, and
computer science itself becomes
no more (and no less) than the discipline of constructing appropriate
descriptive languages.
We now embark on a tour of the technology by which languages are
established in terms of other languages. In this chapter we shall use
Lisp as a base, implementing evaluators as Lisp procedures.
Lisp is
particularly well suited to this task, because of its ability to
represent and manipulate symbolic expressions. We will take the first
step in understanding how languages are implemented by building an
evaluator for Lisp itself. The language implemented by our evaluator
will be a subset of the Scheme dialect of Lisp that we use in this
book. Although the evaluator described in this chapter is written for
a particular dialect of Lisp, it contains the essential structure of
an evaluator for any expression-oriented language designed for writing
programs for a sequential machine. (In fact, most language processors
contain, deep within them, a little “Lisp” evaluator.) The
evaluator has been simplified for the purposes of illustration and
discussion, and some features have been left out that would be
important to include in a production-quality Lisp system.
Nevertheless, this simple evaluator is adequate to execute most of the
programs in this book.
2
An important advantage of making the evaluator accessible as a Lisp
program is that we can implement alternative evaluation rules by
describing these as modifications to the evaluator program. One place
where we can use this power to good effect is to gain extra control
over the ways in which computational models embody the notion of time,
which was so central to the discussion in chapter 3. There, we
mitigated some of the complexities of state and assignment by using
streams to decouple the representation of time in the world from time
in the computer. Our stream programs, however, were
sometimes cumbersome, because they were constrained by
the applicative-order evaluation of Scheme.
In section
4.2
, we'll change
the underlying language to provide for a more elegant approach, by modifying
the evaluator to provide for
normal-order evaluation
.
Section
4.3
implements a more
ambitious linguistic change, whereby expressions have many values,
rather than just a single value. In this language of
nondeterministic computing
, it is natural to express processes that
generate all possible values for expressions and then search for those
values that satisfy certain constraints. In terms of models of
computation and time, this is like having time branch into a set of
“possible futures” and then searching for appropriate time lines.
With our nondeterministic evaluator, keeping track of multiple values
and performing searches are handled automatically by the underlying
mechanism of the language.
In section
4.4
we implement a
logic-programming
language in which knowledge is expressed in terms
of relations, rather than in terms of computations with inputs and
outputs. Even though this makes the language drastically different
from Lisp, or indeed from any conventional language, we will see that
the logic-programming evaluator shares the essential structure of the
Lisp evaluator.
1
The same idea
is pervasive throughout all of engineering. For example, electrical
engineers use many different languages for describing circuits. Two
of these are the language of electrical
networks
and the
language of electrical
systems
. The network language emphasizes
the physical modeling of devices in terms of discrete electrical
elements. The primitive objects of the network language are primitive
electrical components such as resistors, capacitors, inductors, and
transistors, which are characterized in terms of physical variables
called voltage and current. When describing circuits in the network
language, the engineer is concerned with the physical characteristics
of a design. In contrast, the primitive objects of the system
language are signal-processing modules such as filters and amplifiers.
Only the functional behavior of the modules is relevant, and signals
are manipulated without concern for their physical realization as
voltages and currents. The system language is erected on the network
language, in the sense that the elements of signal-processing systems
are constructed from electrical networks. Here, however, the concerns
are with the large-scale organization of electrical devices to solve a
given application problem; the physical feasibility of the parts is
assumed. This layered collection of languages is another example of
the stratified design technique illustrated by the picture
language of section
2.2.4
.
2
The most important features that our evaluator leaves out
are mechanisms for handling errors and supporting debugging. For a
more extensive discussion of evaluators, see
Friedman, Wand, and Haynes
1992, which gives an exposition of programming languages that proceeds
via a sequence of evaluators written in Scheme.
Our evaluator for Lisp will be implemented as a Lisp program. It may
seem circular to think about evaluating Lisp programs using an
evaluator that is itself implemented in Lisp. However, evaluation is
a process, so it is appropriate to describe the evaluation process
using Lisp, which, after all, is our tool for describing
processes.
3
An evaluator that is written in the same language
that it evaluates is said to be
metacircular
.
The metacircular evaluator is essentially a Scheme formulation of the
environment model of evaluation described in
section
3.2
. Recall that the model has two
basic parts:
1. To evaluate a combination (a compound expression other than a
special form), evaluate the subexpressions and then apply the value of
the operator subexpression to the values of the operand
subexpressions.2. To apply a compound procedure to a set of arguments, evaluate the
body of the procedure in a new environment. To construct this
environment, extend the environment part of the procedure object by a
frame in which the formal parameters of the procedure are bound to the
arguments to which the procedure is applied.
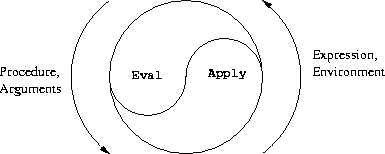
These two rules describe the essence of the evaluation process, a
basic cycle in which expressions to be evaluated in environments are
reduced to procedures to be applied to arguments, which in turn are
reduced to new expressions to be evaluated in new environments, and so
on, until we get down to symbols, whose values are looked
up in the environment, and to primitive procedures, which are applied
directly (see figure
4.1
).
4
This evaluation cycle will be embodied by the interplay between the two
critical procedures in the evaluator,
eval
and
apply
,
which are described in section
4.1.1
(see figure
4.1
).
The implementation of the evaluator will depend upon procedures that
define the
syntax
of the expressions to be evaluated. We will
use
data abstraction to make the evaluator independent of the
representation of the language. For example, rather than committing
to a choice that an assignment is to be represented by a list
beginning with the symbol
set!
we use an abstract predicate
assignment?
to test for an assignment, and we use abstract
selectors
assignment-variable
and
assignment-value
to
access the parts of an assignment. Implementation of expressions will
be described in detail in section
4.1.2
.
There are also operations, described in
section
4.1.3
, that specify the
representation of procedures and environments. For example,
make-procedure
constructs compound procedures,
lookup-variable-value
accesses the values of variables, and
apply-primitive-procedure
applies a primitive procedure to a given list
of arguments.
 |