Structure and Interpretation of Computer Programs (33 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

b. Do the two procedures have the same order of growth in the number
of steps required to convert a balanced tree with
n
elements to a list?
If not, which one grows more slowly?
Exercise 2.64.
The following procedure
list->tree
converts an ordered list to a
balanced binary tree. The helper procedure
partial-tree
takes
as arguments an integer
n
and list of at least
n
elements and
constructs a balanced tree containing the first
n
elements of the
list. The result returned by
partial-tree
is a pair (formed
with
cons
) whose
car
is the constructed tree and whose
cdr
is the list of elements not included in the tree.
(define (list->tree elements)
(car (partial-tree elements (length elements))))
(define (partial-tree elts n)
(if (= n 0)
(cons '() elts)
(let ((left-size (quotient (- n 1) 2)))
(let ((left-result (partial-tree elts left-size)))
(let ((left-tree (car left-result))
(non-left-elts (cdr left-result))
(right-size (- n (+ left-size 1))))
(let ((this-entry (car non-left-elts))
(right-result (partial-tree (cdr non-left-elts)
right-size)))
(let ((right-tree (car right-result))
(remaining-elts (cdr right-result)))
(cons (make-tree this-entry left-tree right-tree)
remaining-elts))))))))
a. Write a short paragraph explaining as clearly as you can how
partial-tree
works. Draw the tree produced by
list->tree
for
the list
(1 3 5 7 9 11)
.
b. What is the order of growth in the number of steps required by
list->tree
to convert a list of
n
elements?
Exercise 2.65.
Use the results of exercises
2.63
and
2.64
to give θ(
n
) implementations of
union-set
and
intersection-set
for sets implemented as
(balanced) binary trees.
41
We have examined options for using lists to represent sets and have
seen how the choice of representation for a data object can have a
large impact on the performance of the programs that use the data.
Another reason for concentrating on sets is that the techniques
discussed here appear again and again in applications involving
information retrieval.
Consider a data base containing a large number of individual records,
such as the personnel files for a company or the transactions in an
accounting system. A typical data-management system spends a large
amount of time accessing or modifying the data in the records and
therefore requires an efficient method for accessing records. This is
done by identifying a part of each record to serve as an identifying
key
. A key can be anything that uniquely identifies the
record. For a personnel file, it might be an employee's ID number.
For an accounting system, it might be a transaction number. Whatever
the key is, when we define the record as a data structure we should
include a
key
selector procedure that retrieves the key
associated with a given record.
Now we represent the data base as a set of records. To locate the
record with a given key we use a procedure
lookup
, which takes
as arguments a key and a data base and which returns the record that
has that key, or false if there is no such record.
Lookup
is implemented in almost the same way as
element-of-set?
. For
example, if the set of records is implemented as an unordered list, we
could use
(define (lookup given-key set-of-records)
(cond ((null? set-of-records) false)
((equal? given-key (key (car set-of-records)))
(car set-of-records))
(else (lookup given-key (cdr set-of-records)))))
Of course, there are better ways to represent large sets than as
unordered lists. Information-retrieval systems in which records have
to be “randomly accessed” are typically implemented by a tree-based
method, such as the binary-tree representation discussed previously.
In designing such a system the methodology of data abstraction
can be a great help. The designer can create an initial
implementation using a simple, straightforward representation such as
unordered lists. This will be unsuitable for the eventual system, but
it can be useful in providing a “quick and dirty” data base with
which to test the rest of the system. Later on, the data
representation can be modified to be more sophisticated. If the data
base is accessed in terms of abstract selectors and constructors, this
change in representation will not require any changes to the rest of
the system.
Exercise 2.66.
Implement the
lookup
procedure for the case
where the set of records is structured as a binary tree, ordered by
the numerical values of the keys.
This section provides practice in the use of list structure and data
abstraction to manipulate sets and trees. The application is to
methods for representing data as sequences of ones and zeros (bits).
For example, the
ASCII standard code used to represent text in
computers encodes each
character as a sequence of seven bits. Using
seven bits allows us to distinguish 2
7
, or 128, possible different
characters. In general, if we want to distinguish
n
different
symbols, we will need to use
log
2
n
bits per symbol. If all our
messages are made up of the eight symbols A, B, C, D, E, F, G, and H,
we can choose a code with three bits per character, for example
| A 000 | C 010 | E 100 | G 110 |
| B 001 | D 011 | F 101 | H 111 |
BACADAEAFABBAAAGAH
is encoded as the string of 54 bits
001000010000011000100000101000001001000000000110000111
Codes such as ASCII and the A-through-H code above are known as
fixed-length
codes, because they represent each symbol in the message
with the same number of bits. It is sometimes advantageous to use
variable-length
codes, in which different symbols may be
represented by different numbers of bits. For example,
Morse code
does not use the same number of dots and dashes for each letter of the
alphabet. In particular, E, the most frequent letter, is represented
by a single dot. In general, if our messages are such that some
symbols appear very frequently and some very rarely, we can encode
data more efficiently (i.e., using fewer bits per message) if we
assign shorter codes to the frequent symbols. Consider the following
alternative code for the letters A through H:
| A 0 | C 1010 | E 1100 | G 1110 |
| B 100 | D 1011 | F 1101 | H 1111 |
100010100101101100011010100100000111001111
This string contains 42 bits, so it saves more than 20% in space in
comparison with the fixed-length code shown above.
One of the difficulties of using a variable-length code is knowing
when you have reached the end of a symbol in reading a sequence of
zeros and ones. Morse code solves this problem by using a special
separator code
(in this case, a pause) after the sequence of
dots and dashes for each letter. Another solution is to design the
code in such a way that no complete code for any symbol is the
beginning (or
prefix
) of the code for another symbol. Such a
code is called a
prefix code
. In the example above, A is
encoded by 0 and B is encoded by 100, so no other symbol can have a
code that begins with 0 or with 100.
In general, we can attain significant savings if we use
variable-length prefix codes that take advantage of the relative
frequencies of the symbols in the messages to be encoded. One
particular scheme for doing this is called the Huffman encoding
method, after its discoverer,
David Huffman. A Huffman code can be
represented as a
binary tree whose leaves are the symbols that are
encoded. At each non-leaf node of the tree there is a set containing
all the symbols in the leaves that lie below the node. In addition,
each symbol at a leaf is assigned a weight (which is its
relative frequency), and each non-leaf
node contains a weight that is the sum of all the weights of the
leaves lying below it. The weights are not used in the encoding or
the decoding process. We will see below how they are used to help
construct the tree.
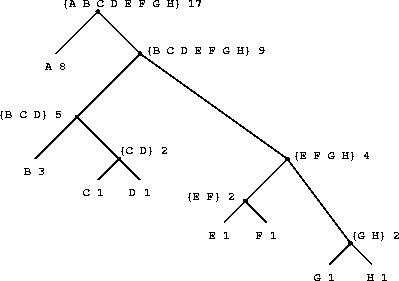 |
Figure
2.18
shows the Huffman tree for the A-through-H
code given above. The weights at the leaves
indicate that the tree was designed for messages in which A appears
with relative frequency 8, B with relative frequency 3, and the
other letters each with relative frequency 1.
Given a Huffman tree, we can find the encoding of any symbol by
starting at the root and moving down until we reach the leaf that
holds the symbol. Each time we move down a left branch we add a 0 to
the code, and each time we move down a right branch we add a 1. (We
decide which branch to follow by testing to see which branch either is
the leaf node for the symbol or contains the symbol in its set.) For
example, starting from the root of the tree in
figure
2.18
, we arrive at the leaf for D by following a
right branch, then a left branch, then a right branch, then a right
branch; hence, the code for D is 1011.
To decode a bit sequence using a Huffman tree, we begin at the root
and use the successive zeros and ones of the bit sequence to determine
whether to move down the left or the right branch. Each time we come
to a leaf, we have generated a new symbol in the message, at which
point we start over from the root of the tree to find the next symbol.
For example, suppose we are given the tree above and the sequence
10001010. Starting at the root, we move down the right branch, (since
the first bit of the string is 1), then down the left branch (since
the second bit is 0), then down the left branch (since the third bit
is also 0). This brings us to the leaf for B, so the first symbol of
the decoded message is B. Now we start again at the root, and we make
a left move because the next bit in the string is 0. This brings us
to the leaf for A. Then we start again at the root with the rest of
the string 1010, so we move right, left, right, left and reach C.
Thus, the entire message is BAC.
Given an “alphabet” of symbols and their relative frequencies, how
do we construct the “best” code? (In other words, which tree will
encode messages with the fewest bits?) Huffman gave an algorithm for
doing this and showed that the resulting code is indeed the best
variable-length code for messages where the relative frequency of the
symbols matches the frequencies with which the code was constructed.
We will not prove this optimality of Huffman codes here, but we will
show how Huffman trees are constructed.
42
The algorithm for generating a Huffman tree is very simple. The idea
is to arrange the tree so that the symbols with the lowest frequency
appear farthest away from the root. Begin with the set of leaf nodes,
containing symbols and their frequencies, as determined by the initial data
from which the code is to be constructed. Now find two leaves with
the lowest weights and merge them to produce a node that has these
two nodes as its left and right branches. The weight of the new node
is the sum of the two weights. Remove the two leaves from the
original set and replace them by this new node. Now continue this
process. At each step, merge two nodes with the smallest weights,
removing them from the set and replacing them with a node that has
these two as its left and right branches. The process stops when
there is only one node left, which is the root of the entire tree.
Here is how the Huffman tree of figure
2.18
was generated:
| Initial leaves | {(A 8) (B 3) (C 1) (D 1) (E 1) (F 1) (G 1) (H 1)} |
Merge | {(A 8) (B 3) ({C D} 2) (E 1) (F 1) (G 1) (H 1)} |
Merge | {(A 8) (B 3) ({C D} 2) ({E F} 2) (G 1) (H 1)} |
Merge | {(A 8) (B 3) ({C D} 2) ({E F} 2) ({G H} 2)} |
Merge | {(A 8) (B 3) ({C D} 2) ({E F G H} 4)} |
Merge | {(A 8) ({B C D} 5) ({E F G H} 4)} |
Merge | {(A 8) ({B C D E F G H} 9)} |
Final merge | {({A B C D E F G H} 17)} |