Structure and Interpretation of Computer Programs (29 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

Exercise 2.50.
Define the transformation
flip-horiz
, which flips
painters horizontally, and transformations that rotate
painters counterclockwise by 180 degrees and 270 degrees.
Exercise 2.51.
Define the
below
operation for painters.
Below
takes two
painters as arguments. The resulting painter, given a frame,
draws with the first painter in the
bottom of the frame and with the second painter in the top. Define
below
in two different ways – first by writing a procedure that is
analogous to the
beside
procedure given above, and
again in terms of
beside
and suitable
rotation operations (from exercise
2.50
).
The picture language exercises some of the critical ideas
we've introduced about abstraction with procedures and data. The
fundamental data abstractions, painters, are implemented using
procedural representations, which enables the language to
handle different basic drawing capabilities in a uniform way. The
means of combination satisfy the closure property, which permits us to
easily build up complex designs. Finally, all the tools for
abstracting procedures are available to us for abstracting means of
combination for painters.
We have also obtained a glimpse of another crucial idea about
languages and program design. This is the approach of
stratified
design
, the notion that a complex system should be structured as a
sequence of levels that are described using a sequence of languages.
Each level is constructed by combining parts that are regarded as
primitive at that level, and the parts constructed at each level are
used as primitives at the next level. The language used at each level
of a stratified design has primitives, means of combination, and means
of abstraction appropriate to that level of detail.
Stratified design pervades the engineering of complex systems. For
example, in computer engineering, resistors and transistors are
combined (and described using a language of analog circuits) to
produce parts such as and-gates and or-gates, which form the
primitives of a language for digital-circuit design.
31
These parts are combined to build
processors, bus structures, and memory systems, which are in turn
combined to form computers, using languages appropriate to computer
architecture. Computers are combined to form distributed systems,
using languages appropriate for describing network interconnections,
and so on.
As a tiny example of stratification, our picture language uses
primitive elements (primitive painters) that are created using a
language that specifies points and lines to provide the lists of line
segments for
segments->painter
, or the
shading details for a painter like
rogers
. The bulk of our
description of the picture language focused on combining these
primitives, using geometric combiners such as
beside
and
below
. We also worked at a higher level, regarding
beside
and
below
as primitives to be manipulated in a language whose
operations, such as
square-of-four
, capture common patterns of
combining geometric combiners.
Stratified design helps make programs
robust
, that is, it makes
it likely that small changes in a specification will require
correspondingly small changes in the program. For instance, suppose
we wanted to change the image based on
wave
shown in
figure
2.9
. We could work at the lowest level
to change the detailed appearance of the
wave
element; we could
work at the middle level to change the way
corner-split
replicates the
wave
; we could work at the highest level to
change how
square-limit
arranges the four copies of the corner.
In general, each level of a stratified design provides a different
vocabulary for expressing the characteristics of the system, and a
different kind of ability to change it.
Exercise 2.52.
Make changes to the square limit of
wave
shown in
figure
2.9
by working at each of the levels
described above. In particular:
a. Add some segments to the primitive
wave
painter
of exercise
2.49
(to add a smile, for example).
b. Change the pattern constructed by
corner-split
(for example, by using only one copy of the
up-split
and
right-split
images instead of two).
c. Modify the version of
square-limit
that uses
square-of-four
so as to assemble the corners in a different pattern. (For example, you
might make the big Mr. Rogers look outward from each corner of the square.)
6
The use of the word
“closure” here comes from abstract algebra,
where a set of elements is said to be closed under an operation if
applying the operation to elements in the set produces an element that
is again an element of the set. The Lisp community
also (unfortunately) uses the word “closure” to describe a totally unrelated
concept: A closure is an implementation technique for representing
procedures with free variables. We do not use the word “closure” in
this second sense in this book.
7
The notion that a means of
combination should satisfy closure is a straightforward idea.
Unfortunately, the data combiners provided in many popular programming
languages do not satisfy closure, or make closure cumbersome to
exploit. In
Fortran or
Basic, one typically combines data elements by
assembling them into arrays – but one cannot form arrays whose
elements are themselves arrays.
Pascal and
C admit structures whose
elements are structures. However, this requires that the programmer
manipulate pointers explicitly, and adhere to the restriction that
each field of a structure can contain only elements of a prespecified form.
Unlike
Lisp with its pairs, these languages have no built-in general-purpose
glue that makes it easy to manipulate compound data in a uniform way.
This limitation lies behind Alan
Perlis's comment in his foreword to
this book: “In Pascal the plethora of declarable data structures
induces a specialization within functions that inhibits and penalizes
casual cooperation. It is better to have 100 functions operate on one
data structure than to have 10 functions operate on 10 data
structures.”
8
In this book, we use
list
to mean a chain of
pairs terminated by the end-of-list marker. In contrast, the term
list structure
refers to any data structure made out of pairs,
not just to lists.
9
Since nested applications of
car
and
cdr
are cumbersome to write, Lisp dialects provide abbreviations for
them – for instance,
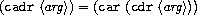
The names of all such procedures start with
c
and end with
r
. Each
a
between them stands for a
car
operation and
each
d
for a
cdr
operation, to be applied in the same order
in which they appear in the name. The names
car
and
cdr
persist because simple combinations like
cadr
are
pronounceable.
10
It's remarkable how much energy in the
standardization of Lisp dialects has been dissipated in arguments that
are literally over nothing: Should
nil
be an ordinary name?
Should the value of
nil
be a symbol? Should it be a list?
Should it be a pair?
In Scheme,
nil
is an ordinary name,
which we use in this section as a variable whose value is
the end-of-list marker (just as
true
is an ordinary variable
that has a true value). Other dialects of
Lisp, including Common Lisp, treat
nil
as a special symbol. The
authors of this book, who have endured too many language
standardization brawls, would like to avoid the entire issue. Once we
have introduced quotation in section
2.3
, we will
denote the empty list as
'()
and dispense with the
variable
nil
entirely.
11
To define
f
and
g
using
lambda
we would write
(define f (lambda (x y . z) <
body
>))
(define g (lambda w <
body
>))
12
Scheme
standardly provides a
map
procedure that is more general
than the one described here.
This more general
map
takes a procedure of
n
arguments, together with
n
lists, and
applies the procedure to all the first elements of
the lists, all the second elements of the lists, and so on,
returning a list of the results. For example:
(map + (list 1 2 3) (list 40 50 60) (list 700 800 900))
(741 852 963)
(map (lambda (x y) (+ x (* 2 y)))
(list 1 2 3)
(list 4 5 6))
(9 12 15)
13
The order of the
first two clauses in the
cond
matters, since the empty list
satisfies
null?
and also is not a pair.
14
This is, in fact, precisely the
fringe
procedure from
exercise
2.28
. Here we've renamed it to emphasize that
it is part of a family of general sequence-manipulation procedures.
15
Richard Waters (1979)
developed a program that automatically analyzes traditional
Fortran
programs, viewing them in terms of maps, filters, and accumulations.
He found that fully 90 percent of the code in the Fortran Scientific
Subroutine Package fits neatly into this paradigm. One of the reasons
for the success of Lisp as a programming language is that lists
provide a standard medium for expressing ordered collections so that
they can be manipulated using higher-order operations. The
programming language
APL owes much of its power and appeal to a
similar choice. In APL all data are represented as arrays, and there is a
universal and convenient set of generic operators for all sorts of
array operations.
16
According to
Knuth (1981), this rule was formulated by
W. G. Horner early in the nineteenth century, but the method was
actually used by Newton over a hundred years earlier. Horner's rule
evaluates the polynomial using fewer additions and multiplications
than does the straightforward method of first computing
a
n
x
n
,
then adding
a
n
-1
x
n
-1
, and so on. In fact, it is possible to
prove that any algorithm for evaluating arbitrary polynomials must use
at least as many additions and multiplications as does Horner's rule,
and thus Horner's rule is an
optimal algorithm for polynomial
evaluation. This was proved (for the number of additions) by
A. M. Ostrowski in a 1954 paper that essentially founded the modern
study of optimal algorithms. The analogous statement for
multiplications was proved by
V. Y. Pan in 1966. The book by
Borodin
and
Munro (1975) provides an overview of these and other results about
optimal algorithms.
17
This definition uses the
extended version of
map
described in footnote
12
.
18
This approach to nested mappings was shown
to us by
David Turner, whose languages
KRC and
Miranda provide elegant
formalisms for dealing with these constructs. The examples in this
section (see also exercise
2.42
) are adapted from Turner
1981. In section
3.5.3
, we'll see how this
approach generalizes to infinite sequences.
19
We're
representing a pair here as a list of two elements rather than as a
Lisp pair. Thus, the “pair” (
i
,
j
) is represented as
(list i
j)
, not
(cons i j)
.
20
The set
S
-
x
is the set of all elements
of
S
, excluding
x
.
21
Semicolons in Scheme code are used to
introduce
comments
. Everything from the semicolon to the end of
the line is ignored by the interpreter. In this book we don't use
many comments; we try to make our programs self-documenting by using
descriptive names.
22
The picture language is based on the language
Peter Henderson created to construct
images like
M.C. Escher's “Square Limit” woodcut (see Henderson 1982).
The woodcut incorporates a
repeated scaled pattern, similar to the arrangements drawn using
the
square-limit
procedure in this section.
23
William Barton Rogers (1804-1882) was the founder and first president
of MIT. A geologist and talented teacher, he taught at William and
Mary College and at the University of Virginia. In 1859 he moved to
Boston, where he had more time for research, worked on a plan
for establishing a “polytechnic institute,” and served as
Massachusetts's first State Inspector of Gas Meters.
When MIT was established in 1861, Rogers was elected its first
president. Rogers espoused an ideal of “useful learning” that was
different from the university education of the time, with its
overemphasis on the classics, which, as he wrote, “stand in the way of
the broader, higher and more practical instruction and discipline of
the natural and social sciences.” This education was likewise to be
different from narrow trade-school education. In Rogers's words:
The world-enforced distinction between the practical and the
scientific worker is utterly futile, and the whole experience of
modern times has demonstrated its utter worthlessness.
Rogers served as president of MIT until 1870, when he resigned due to
ill health. In 1878 the second president of MIT,
John Runkle,
resigned under the pressure of a financial crisis brought on by the
Panic of 1873 and strain of fighting off attempts by Harvard to take
over MIT. Rogers returned to hold the office of president until
1881.
Rogers collapsed and died while addressing MIT's graduating class at
the commencement exercises of 1882. Runkle quoted Rogers's last
words in a memorial address delivered that same year:
In the words of Francis A. Walker“As I stand here today and see what the Institute is,
...
I call
to mind the beginnings of science. I remember one hundred and fifty
years ago Stephen Hales published a pamphlet on the subject of
illuminating gas, in which he stated that his researches had
demonstrated that 128 grains of bituminous coal – ”“Bituminous coal,” these were his last words on earth. Here he bent
forward, as if consulting some notes on the table before him, then
slowly regaining an erect position, threw up his hands, and was
translated from the scene of his earthly labors and triumphs to “the
tomorrow of death,” where the mysteries of life are solved, and the
disembodied spirit finds unending satisfaction in contemplating the
new and still unfathomable mysteries of the infinite future.
(MIT's third president):
All his life he had borne himself most faithfully and heroically, and
he died as so good a knight would surely have wished, in harness, at
his post, and in the very part and act of public duty.
24
Equivalently, we could
write
(define flipped-pairs
(square-of-four identity flip-vert identity flip-vert))
25
Rotate180
rotates a painter by 180 degrees (see exercise
2.50
).
Instead of
rotate180
we could say
(compose flip-vert flip-horiz)
, using
the
compose
procedure from exercise
1.42
.
26
Frame-coord-map
uses
the vector operations described in exercise
2.46
below, which we
assume have been implemented using some representation for vectors.
Because of data abstraction, it doesn't matter what this vector
representation is, so long as the vector operations behave correctly.
27
Segments->painter
uses the representation for line
segments described in exercise
2.48
below.
It also uses the
for-each
procedure described in exercise
2.23
.
28
For example, the
rogers
painter of
figure
2.11
was constructed from a gray-level image.
For each point in a given frame,
the
rogers
painter determines the point in the image that is mapped to it
under the frame coordinate map, and shades it
accordingly. By allowing different types of painters, we are capitalizing on the
abstract data idea discussed in section
2.1.3
, where we
argued that a rational-number representation could be anything at all that
satisfies an appropriate condition. Here we're using the fact that a
painter can be implemented in any way at all, so long as it draws
something in the designated frame. Section
2.1.3
also
showed how pairs could be implemented as procedures. Painters are our
second example of a procedural representation for data.