Structure and Interpretation of Computer Programs (31 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

This
deriv
procedure incorporates the complete differentiation algorithm.
Since it is expressed in terms of abstract data, it will work no
matter how we choose to represent algebraic expressions, as long as we
design a proper set of selectors and constructors. This is the issue
we must address next.
We can imagine many ways to use list structure to represent algebraic
expressions. For example, we could use lists of symbols that mirror
the usual algebraic notation, representing
a
x
+
b
as the list
(a
* x + b)
. However, one especially straightforward choice is to use
the same parenthesized prefix notation that Lisp uses for
combinations; that is, to represent
a
x
+
b
as
(+ (* a x) b)
.
Then our data representation for the differentiation problem is as
follows:
- The variables are symbols. They are identified by the primitive predicate
symbol?
:(define (variable? x) (symbol? x))
- Two variables are the same if the symbols representing them are
eq?
:(define (same-variable? v1 v2)
(and (variable? v1) (variable? v2) (eq? v1 v2))) - Sums and products are constructed as lists:
(define (make-sum a1 a2) (list '+ a1 a2))
(define (make-product m1 m2) (list '* m1 m2)) - A sum is a list whose first element is the symbol
+
:(define (sum? x)
(and (pair? x) (eq? (car x) '+))) - The addend is the second item of the sum list:
(define (addend s) (cadr s))
- The augend is the third item of the sum list:
(define (augend s) (caddr s))
- A product is a list whose first element is the symbol
*
:(define (product? x)
(and (pair? x) (eq? (car x) '*))) - The multiplier is the second item of the product list:
(define (multiplier p) (cadr p))
- The multiplicand is the third item of the product list:
(define (multiplicand p) (caddr p))
Thus, we need only combine these with the algorithm as embodied by
deriv
in order to have a working symbolic-differentiation
program. Let us look at some examples of its behavior:
(deriv '(+ x 3) 'x)
(+ 1 0)
(deriv '(* x y) 'x)
(+ (* x 0) (* 1 y))
(deriv '(* (* x y) (+ x 3)) 'x)
(+ (* (* x y) (+ 1 0))
(* (+ (* x 0) (* 1 y))
(+ x 3)))
The program produces answers that are correct; however, they are
unsimplified. It is true that
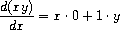
but we would like the program to know that
x
· 0 = 0, 1 ·
y
=
y
, and 0 +
y
=
y
. The answer for the second example should have been
simply
y
. As the third example shows, this becomes a serious
issue when the expressions are complex.
Our difficulty is much like the one we encountered with the
rational-number implementation: we haven't reduced answers to simplest
form. To accomplish the rational-number reduction, we needed to
change only the constructors and the selectors of the implementation.
We can adopt a similar strategy here. We won't change
deriv
at
all. Instead, we will change
make-sum
so that if both summands
are numbers,
make-sum
will add them and return their sum. Also,
if one of the summands is 0, then
make-sum
will return the other
summand.
(define (make-sum a1 a2)
(cond ((=number? a1 0) a2)
((=number? a2 0) a1)
((and (number? a1) (number? a2)) (+ a1 a2))
(else (list '+ a1 a2))))
This uses the procedure
=number?
, which checks whether an
expression is equal to a given number:
(define (=number? exp num)
(and (number? exp) (= exp num)))
Similarly, we will change
make-product
to build in the rules that 0
times anything is 0 and 1 times anything is the thing itself:
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0)) 0)
((=number? m1 1) m2)
((=number? m2 1) m1)
((and (number? m1) (number? m2)) (* m1 m2))
(else (list '* m1 m2))))
Here is how this version works on our three examples:
(deriv '(+ x 3) 'x)
1
(deriv '(* x y) 'x)
y
(deriv '(* (* x y) (+ x 3)) 'x)
(+ (* x y) (* y (+ x 3)))
Although this is quite an improvement, the third example shows that
there is still a long way to go before we get a program that puts
expressions into a form that we might agree is “simplest.” The
problem of algebraic simplification is complex because, among other
reasons, a form that may be simplest for one purpose may not be for
another.
Exercise 2.56.
Show how to extend the basic differentiator to handle more kinds of
expressions. For instance, implement the differentiation rule
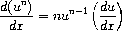
by adding a new clause to the
deriv
program
and defining
appropriate procedures
exponentiation?
,
base
,
exponent
,
and
make-exponentiation
. (You may use the symbol
**
to denote
exponentiation.)
Build in the rules that anything raised to the power 0 is 1 and
anything raised to the power 1 is the thing itself.
Exercise 2.57.
Extend the differentiation program to handle sums and products of
arbitrary numbers of (two or more) terms.
Then the last example above could be expressed as
(deriv '(* x y (+ x 3)) 'x)
Try to do this by changing only the
representation for sums and products, without changing the
deriv
procedure at all. For example, the
addend
of a sum would
be the first term, and the
augend
would be the sum of the rest
of the terms.
Exercise 2.58.
Suppose we want to modify the differentiation program so that it works
with ordinary mathematical notation, in which
+
and
*
are
infix rather than prefix operators. Since the differentiation program
is defined in terms of abstract data, we can modify it to work with
different representations of expressions solely by changing the
predicates, selectors, and constructors that define the representation
of the algebraic expressions on which the differentiator is to
operate.
a. Show how to do this in order to differentiate algebraic
expressions presented in infix form, such as
(x + (3 * (x + (y + 2))))
.
To simplify the task, assume that
+
and
*
always
take two arguments and that expressions are fully parenthesized.
b. The problem becomes substantially harder if we allow standard
algebraic notation, such as
(x + 3 * (x + y + 2))
, which drops
unnecessary parentheses and assumes that multiplication is done before
addition. Can you design appropriate predicates, selectors, and
constructors for this notation such that our derivative program still
works?
In the previous examples we built representations for two kinds of
compound data objects: rational numbers and algebraic expressions. In
one of these examples we had the choice of simplifying (reducing) the
expressions at either construction time or selection time, but other
than that the choice of a representation for these structures in terms
of lists was straightforward. When we turn to the representation of
sets, the choice of a representation is not so obvious. Indeed, there
are a number of possible representations, and they differ
significantly from one another in several ways.
Informally, a set is simply a collection of distinct objects. To give
a more precise definition we can employ the method of data
abstraction. That is, we define “set” by specifying the operations
that are to be used on sets. These are
union-set
,
intersection-set
,
element-of-set?
, and
adjoin-set
.
Element-of-set?
is a predicate that determines whether a given
element is a member of a set.
Adjoin-set
takes an object and a
set as arguments and returns a set that contains the elements of the
original set and also the adjoined element.
Union-set
computes
the union of two sets, which is the set containing each element that
appears in either argument.
Intersection-set
computes the
intersection of two sets, which is the set containing only elements
that appear in both arguments. From the viewpoint of data abstraction, we
are free to design any representation that implements these operations
in a way consistent with the interpretations given above.
37
One way to represent a set is as a list of its elements in which no
element appears more than once. The empty set is represented by the
empty list. In this representation,
element-of-set?
is similar
to the procedure
memq
of section
2.3.1
. It uses
equal?
instead of
eq?
so that the set elements need not be symbols:
(define (element-of-set? x set)
(cond ((null? set) false)
((equal? x (car set)) true)
(else (element-of-set? x (cdr set)))))
Using this, we can write
adjoin-set
. If the object to be adjoined
is already in the set, we just return the set. Otherwise, we use
cons
to add the object to the list that represents the set:
(define (adjoin-set x set)
(if (element-of-set? x set)
set
(cons x set)))
For
intersection-set
we can use a recursive strategy. If we
know how to form the intersection of
set2
and the
cdr
of
set1
, we only need to decide whether to include
the
car
of
set1
in this. But this depends on whether
(car
set1)
is also in
set2
. Here is the resulting procedure:
(define (intersection-set set1 set2)
(cond ((or (null? set1) (null? set2)) '())
((element-of-set? (car set1) set2)
(cons (car set1)
(intersection-set (cdr set1) set2)))
(else (intersection-set (cdr set1) set2))))
In designing a representation, one of the issues we should be
concerned with is efficiency. Consider the number of steps required by our set
operations. Since they all use
element-of-set?
, the speed
of this operation has a major impact on the efficiency of the set
implementation as a whole. Now, in order to check whether an object
is a member of a set,
element-of-set?
may have to scan the
entire set. (In the worst case, the object turns out not to be in the
set.) Hence, if the set has
n
elements,
element-of-set?
might take up to
n
steps. Thus, the number of steps
required grows as θ(
n
).
The number of steps required by
adjoin-set
, which uses this operation,
also grows as θ(
n
). For
intersection-set
, which does an
element-of-set?
check for each element of
set1
, the number of steps
required grows as the product of the sizes of the sets involved, or
θ(
n
2
) for two sets of size
n
. The same will be true of
union-set
.
Exercise 2.59.
Implement the
union-set
operation for the unordered-list
representation of sets.