Structure and Interpretation of Computer Programs (28 page)

Exercise 2.45.
  
Right-split
and
up-split
can be expressed as
instances of a general splitting operation.
Define a procedure
split
with the property that evaluating

(define right-split (split beside below))
(define up-split (split below beside))

produces procedures
right-split
and
up-split
with the same
behaviors as the ones already defined.

Before we can show how to implement painters and their
means of combination, we must first consider
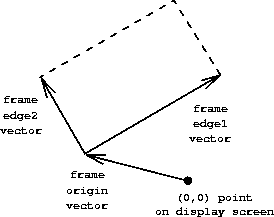
frames. A frame can be described by three vectors – an origin vector
and two edge vectors. The origin vector specifies the offset of the
frame's origin from some absolute origin in the plane, and the edge
vectors specify the offsets of the frame's corners from its origin.
If the edges are perpendicular, the frame will be rectangular.
Otherwise the frame will be a more general parallelogram.

Figure 
2.15
shows a frame and its associated vectors. In
accordance with data abstraction, we need not be
specific yet about how frames are represented, other than to say that
there is a constructor
make-frame
, which takes three vectors and
produces a frame, and three corresponding selectors
origin-frame
,
edge1-frame
, and
edge2-frame
(see
exercise 
2.47
).

Figure 2.15:
  A frame is described by three vectors – an
origin and two edges.

We will use coordinates in the unit square (0
<
x
,
y
<
1)
to specify images.
With each frame, we associate a
frame coordinate map
, which
will be used to shift and scale images to fit the frame. The map
transforms the unit square into the frame by
mapping the vector
v
= (
x
,
y
) to the vector sum

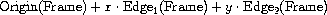
For example, (0,0) is mapped to the origin of the frame, (1,1) to
the vertex diagonally opposite the origin, and (0.5,0.5) to the
center of the frame. We can create a frame's coordinate map with the
following procedure:
²⁶

(define (frame-coord-map frame)
  (lambda (v)
    (add-vect
     (origin-frame frame)
     (add-vect (scale-vect (xcor-vect v)
                           (edge1-frame frame))
               (scale-vect (ycor-vect v)
                           (edge2-frame frame))))))

Observe that applying
frame-coord-map
to a frame returns
a procedure that, given a vector, returns a vector.
If the argument vector is in the unit square, the result vector
will be in the frame. For example,

((frame-coord-map a-frame) (make-vect 0 0))

returns the same vector as

(origin-frame a-frame)

Exercise 2.46.
  
A two-dimensional vector
v
running from the origin to a point
can be represented as a pair
consisting of an
x
-coordinate and a
y
-coordinate. Implement a data
abstraction for vectors by giving a constructor
make-vect
and
corresponding selectors
xcor-vect
and
ycor-vect
. In
terms of your selectors and constructor, implement procedures
add-vect
,
sub-vect
, and
scale-vect
that perform
the operations vector addition, vector subtraction, and multiplying a
vector by a scalar:

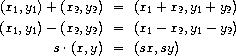
Exercise 2.47.
  Here are two possible constructors for frames:

(define (make-frame origin edge1 edge2)
  (list origin edge1 edge2))
(define (make-frame origin edge1 edge2)
  (cons origin (cons edge1 edge2)))

For each constructor supply the appropriate selectors to produce an
implementation for frames.

A painter is represented as a procedure that, given a frame
as argument, draws a particular image shifted and scaled to fit the frame.
That is to say, if
p
is a painter and
f
is a frame, then we
produce
p
's image in
f
by calling
p
with
f
as
argument.

The details of how primitive painters are implemented depend on the
particular characteristics of the graphics system and the type of
image to be drawn. For instance, suppose we have a procedure
draw-line
that draws a line on the screen between two specified
points. Then we can create painters for line drawings, such as the
wave
painter in figure 
2.10
, from lists of line
segments as follows:
²⁷

(define (segments->painter segment-list)
  (lambda (frame)
    (for-each
     (lambda (segment)
       (draw-line
        ((frame-coord-map frame) (start-segment segment))
        ((frame-coord-map frame) (end-segment segment))))
     segment-list)))

The segments are given using coordinates with respect to the unit
square. For each segment in the list, the painter transforms the
segment endpoints with the frame coordinate map and draws a line
between the transformed points.

Representing painters as procedures erects a powerful abstraction
barrier in the picture language. We can create and intermix
all sorts of primitive painters, based on a variety of graphics
capabilities. The details of their implementation do not matter. Any
procedure can serve as a painter, provided that it takes a frame as
argument and draws something scaled to fit the frame.
²⁸

Exercise 2.48.
  
A directed line segment in the
plane can be represented as a pair of vectors – the
vector running from the origin to the start-point of the segment, and
the vector running from the origin to the end-point of the segment.
Use your vector representation from exercise 
2.46
to
define a representation for segments with a constructor
make-segment
and selectors
start-segment
and
end-segment
.

Exercise 2.49.
  Use
segments->painter
to define the following primitive painters:

a.  The painter that draws the outline of the designated frame.

b.  The painter that draws an “X” by connecting opposite corners of
the frame.

c.  The painter that draws a diamond shape by connecting the midpoints of
the sides of the frame.

d.  The
wave
painter.

An operation on painters (such as
flip-vert
or
beside
)
works by creating a painter that invokes the original painters
with respect to frames derived from the argument frame.
Thus, for example,
flip-vert
doesn't have to know how a painter
works in order to flip it – it just has to know how to turn a frame
upside down:
The flipped painter just uses the original painter,
but in the inverted frame.

Painter operations are based on
the procedure
transform-painter
, which takes as arguments a painter and
information on how to transform a frame and
produces a new painter. The transformed painter, when called on a frame,
transforms the frame and
calls the original painter on the transformed frame.
The arguments to
transform-painter
are points (represented as vectors)
that specify the corners of the new frame:
When mapped into
the frame, the first point specifies the new frame's origin
and the other two specify the ends of its edge vectors.
Thus, arguments within the
unit square specify a frame contained within the original frame.

(define (transform-painter painter origin corner1 corner2)
  (lambda (frame)
    (let ((m (frame-coord-map frame)))
      (let ((new-origin (m origin)))
        (painter
         (make-frame new-origin
                     (sub-vect (m corner1) new-origin)
                     (sub-vect (m corner2) new-origin)))))))

Here's how to flip painter images vertically:

(define (flip-vert painter)
  (transform-painter painter
                     (make-vect 0.0 1.0)   
; new 
origin
                     (make-vect 1.0 1.0)   
; new end of 
edge1
                     (make-vect 0.0 0.0))) 
; new end of 
edge2

Using
transform-painter
, we can easily define new transformations.
For example, we can define a painter that shrinks its image to the
upper-right quarter of the frame it is given:

(define (shrink-to-upper-right painter)
  (transform-painter painter
                     (make-vect 0.5 0.5)
                     (make-vect 1.0 0.5)
                     (make-vect 0.5 1.0)))

Other transformations rotate images counterclockwise by 90 degrees
²⁹

(define (rotate90 painter)
  (transform-painter painter
                     (make-vect 1.0 0.0)
                     (make-vect 1.0 1.0)
                     (make-vect 0.0 0.0)))

or squash images towards the center of the frame:
³⁰

(define (squash-inwards painter)
  (transform-painter painter
                     (make-vect 0.0 0.0)
                     (make-vect 0.65 0.35)
                     (make-vect 0.35 0.65)))

Frame transformation is also the key to
defining means of combining two or more painters.
The
beside
procedure,
for example, takes two painters, transforms them
to paint in the left and right halves of an argument frame respectively,
and produces a new, compound painter.
When the compound painter is given a frame, it
calls the first transformed painter to paint in the left half of
the frame and calls the second transformed painter to paint in the
right half of the frame:

(define (beside painter1 painter2)
  (let ((split-point (make-vect 0.5 0.0)))
    (let ((paint-left
           (transform-painter painter1
                              (make-vect 0.0 0.0)
                              split-point
                              (make-vect 0.0 1.0)))
          (paint-right
           (transform-painter painter2
                              split-point
                              (make-vect 1.0 0.0)
                              (make-vect 0.5 1.0))))
      (lambda (frame)
        (paint-left frame)
        (paint-right frame)))))

Observe how the painter data abstraction, and in particular the
representation of painters as procedures, makes
beside
easy to
implement. The
beside
procedure need not know anything
about the details of the component painters other than that each
painter will draw something in its designated frame.