Structure and Interpretation of Computer Programs (35 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

We have introduced data abstraction, a methodology for structuring
systems in such a way that much of a program can be specified
independent of the choices involved in implementing the data objects
that the program manipulates. For example, we saw in
section
2.1.1
how to separate the task of designing a
program that uses rational numbers from the task of implementing
rational numbers in terms of the computer language's primitive
mechanisms for constructing compound data. The key idea was to erect
an abstraction barrier – in this case, the selectors and constructors
for rational numbers (
make-rat
,
numer
,
denom
) – that
isolates the way rational numbers are used from their underlying
representation in terms of list structure. A similar abstraction
barrier isolates the details of the procedures that perform rational
arithmetic (
add-rat
,
sub-rat
,
mul-rat
, and
div-rat
) from the “higher-level” procedures that use rational
numbers. The resulting program has the structure shown in
figure
2.1
.
These data-abstraction barriers are powerful tools for controlling
complexity. By isolating the underlying representations of data
objects, we can divide the task of designing a large program into
smaller tasks that can be performed separately. But this kind of data
abstraction is not yet powerful enough, because it may not always make
sense to speak of “the underlying representation” for a data object.
For one thing, there might be more than one useful representation for
a data object, and we might like to design systems that can deal with
multiple representations. To take a simple example, complex numbers
may be represented in two almost equivalent ways: in rectangular form
(real and imaginary parts) and in polar form (magnitude and angle).
Sometimes rectangular form is more appropriate and sometimes polar
form is more appropriate. Indeed, it is perfectly plausible to
imagine a system in which complex numbers are represented in both
ways, and in which the procedures for manipulating complex numbers work
with either representation.
More importantly, programming systems are often designed by many
people working over extended periods of time, subject to requirements
that change over time. In such an environment, it is simply not
possible for everyone to agree in advance on choices of data
representation. So in addition to the data-abstraction barriers that
isolate representation from use, we need abstraction barriers that
isolate different design choices from each other and permit different
choices to coexist in a single program. Furthermore, since large
programs are often created by combining pre-existing modules that were
designed in isolation, we need conventions that permit programmers to
incorporate modules into larger systems
additively
, that is,
without having to redesign or reimplement these modules.
In this section, we will learn how to cope with data that may be
represented in different ways by different parts of a program. This
requires constructing
generic procedures
– procedures that can
operate on data that may be represented in more than one way. Our
main technique for building generic procedures will be to work in terms
of data objects that have
type tags
, that is, data objects
that include explicit information about how they are to be processed.
We will also discuss
data-directed
programming, a powerful and
convenient implementation strategy for additively assembling systems
with generic operations.
We begin with the simple complex-number example. We will see how
type tags and data-directed style enable us to design separate
rectangular and polar representations for complex numbers while
maintaining the notion of an abstract “complex-number” data object.
We will accomplish this by defining arithmetic procedures for complex
numbers (
add-complex
,
sub-complex
,
mul-complex
, and
div-complex
) in terms of generic selectors that access parts of
a complex number independent of how the number is represented. The
resulting complex-number system, as shown in
figure
2.19
, contains two different kinds of
abstraction barriers. The “horizontal” abstraction barriers play
the same role as the ones in
figure
2.1
. They isolate “higher-level”
operations from “lower-level” representations. In addition, there
is a “vertical” barrier that gives us the ability to separately
design and install alternative representations.
 |
In section
2.5
we will show how to use
type tags and data-directed style to develop a generic arithmetic
package. This provides procedures (
add
,
mul
, and so on)
that can be used to manipulate all sorts of “numbers” and can be
easily extended when a new kind of number is needed.
In section
2.5.3
, we'll show how to use generic
arithmetic in a system that performs symbolic algebra.
We will develop a system that performs arithmetic operations on
complex numbers as a simple but unrealistic example of a program that
uses generic operations. We begin by discussing two plausible
representations for complex numbers as ordered pairs: rectangular form
(real part and imaginary part) and polar form (magnitude and
angle).
43
Section
2.4.2
will show how both representations can be made to coexist in a single
system through the use of type tags and generic operations.
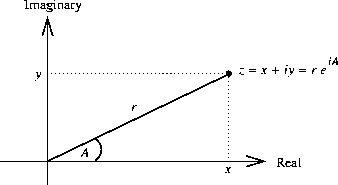
Like rational numbers, complex numbers are naturally represented as
ordered pairs. The set of complex numbers can be thought of as a
two-dimensional space with two orthogonal axes, the “real” axis and
the “imaginary” axis. (See figure
2.20
.) From
this point of view, the complex number
z
=
x
+
i
y
(where
i
2
= - 1)
can be thought of as the point in the plane whose real coordinate is
x
and whose
imaginary coordinate is
y
. Addition of complex numbers reduces in
this representation to addition of coordinates:
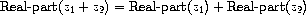
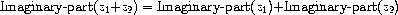
When multiplying complex numbers, it is more natural to think in terms
of representing a complex number in polar form, as a magnitude and an
angle (
r
and
A
in figure
2.20
).
The product of two complex numbers is the vector obtained by
stretching one complex number by the length of the other and then
rotating it through the angle of the other:
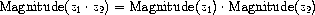
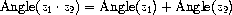
Thus, there are two different representations for complex numbers,
which are appropriate for different operations. Yet, from the
viewpoint of someone writing a program that uses complex numbers, the
principle of data abstraction suggests that all the operations for
manipulating complex numbers should be available regardless of which
representation is used by the computer. For example, it is often
useful to be able to find the magnitude of a complex number that is
specified by rectangular coordinates. Similarly, it is often useful
to be able to determine the real part of a complex number that is
specified by polar coordinates.
 |
To design such a system, we can follow the same
data-abstraction
strategy we followed in designing the rational-number package in
section
2.1.1
. Assume that the operations on complex numbers are
implemented in terms of four selectors:
real-part
,
imag-part
,
magnitude
, and
angle
. Also assume that
we have two procedures for constructing complex numbers:
make-from-real-imag
returns a complex number with specified real and
imaginary parts, and
make-from-mag-ang
returns a complex number with
specified magnitude and angle. These procedures have the property that,
for any complex number
z
, both