Structure and Interpretation of Computer Programs (73 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

To implement these operations we represent an environment as a list of
frames. The enclosing environment of an environment is the
cdr
of
the list. The empty environment is simply the empty list.
(define (enclosing-environment env) (cdr env))
(define (first-frame env) (car env))
(define the-empty-environment '())
Each frame of an environment is represented as a pair of lists: a list
of the variables bound in that frame and a list of the associated values.
14
(define (make-frame variables values)
(cons variables values))
(define (frame-variables frame) (car frame))
(define (frame-values frame) (cdr frame))
(define (add-binding-to-frame! var val frame)
(set-car! frame (cons var (car frame)))
(set-cdr! frame (cons val (cdr frame))))
To extend an environment by a new frame that associates variables with
values, we make a frame consisting of the list of variables and the
list of values, and we adjoin this to the environment. We signal
an error if the number of variables does not match the number of values.
(define (extend-environment vars vals base-env)
(if (= (length vars) (length vals))
(cons (make-frame vars vals) base-env)
(if (< (length vars) (length vals))
(error "Too many arguments supplied" vars vals)
(error "Too few arguments supplied" vars vals))))
To look up a variable in an environment, we scan the list of variables
in the first frame. If we find the desired variable, we return
the corresponding element in the list of values. If we do not find
the variable in the current frame, we search the enclosing environment,
and so on. If we reach the empty environment, we signal an “unbound
variable” error.
(define (lookup-variable-value var env)
(define (env-loop env)
(define (scan vars vals)
(cond ((null? vars)
(env-loop (enclosing-environment env)))
((eq? var (car vars))
(car vals))
(else (scan (cdr vars) (cdr vals)))))
(if (eq? env the-empty-environment)
(error "Unbound variable" var)
(let ((frame (first-frame env)))
(scan (frame-variables frame)
(frame-values frame)))))
(env-loop env))
To set a variable to a new value in a specified environment, we scan
for the variable, just as in
lookup-variable-value
, and change
the corresponding value when we find it.
(define (set-variable-value! var val env)
(define (env-loop env)
(define (scan vars vals)
(cond ((null? vars)
(env-loop (enclosing-environment env)))
((eq? var (car vars))
(set-car! vals val))
(else (scan (cdr vars) (cdr vals)))))
(if (eq? env the-empty-environment)
(error "Unbound variable -- SET!" var)
(let ((frame (first-frame env)))
(scan (frame-variables frame)
(frame-values frame)))))
(env-loop env))
To define a variable, we search the first frame for a binding for
the variable, and change the binding if it exists
(just as in
set-variable-value!
). If no such binding
exists, we adjoin one to the first frame.
(define (define-variable! var val env)
(let ((frame (first-frame env)))
(define (scan vars vals)
(cond ((null? vars)
(add-binding-to-frame! var val frame))
((eq? var (car vars))
(set-car! vals val))
(else (scan (cdr vars) (cdr vals)))))
(scan (frame-variables frame)
(frame-values frame))))
The method described here is only one of many plausible ways to
represent environments. Since we used data abstraction to isolate the
rest of the evaluator from the detailed choice of representation, we
could change the environment representation if we wanted to. (See
exercise
4.11
.) In a
production-quality Lisp system, the speed of the evaluator's
environment operations – especially that of variable lookup – has a
major impact on the performance of the system. The representation
described here, although conceptually simple, is not efficient and
would not ordinarily be used in a production system.
15
Exercise 4.11.
Instead of representing a frame as a pair of lists, we can represent a
frame as a list of bindings, where each binding is a name-value pair.
Rewrite the environment operations to use this alternative
representation.
Exercise 4.12.
The procedures
set-variable-value!
,
define-variable!
,
and
lookup-variable-value
can be expressed in terms of
more abstract procedures for traversing the environment structure.
Define abstractions that capture the common patterns and redefine
the three procedures in terms of these abstractions.
Exercise 4.13.
Scheme allows us to create new bindings for variables by means of
define
, but provides no way to get rid of bindings. Implement for
the evaluator a special form
make-unbound!
that removes the
binding of a given symbol from the environment in which the
make-unbound!
expression is evaluated.
This problem is not completely specified. For example,
should we remove only the binding in the first frame of the
environment? Complete the specification and justify any choices you
make.
Given the evaluator, we have in our hands a description
(expressed in Lisp) of the process
by which Lisp expressions are evaluated. One advantage of expressing the
evaluator as a program is that we can run the program. This gives us,
running within Lisp, a working model of how Lisp itself evaluates
expressions. This can serve as a framework for experimenting with
evaluation rules, as we shall do later in this chapter.
Our evaluator program reduces expressions ultimately to the
application of primitive procedures. Therefore, all that we need to
run the evaluator is to create a mechanism that calls on the underlying
Lisp system to model the application of primitive procedures.
There must be a binding for each primitive procedure name, so that when
eval
evaluates the operator of an application of a primitive, it
will find an object to pass to
apply
. We thus set up a
global
environment that associates unique objects with the names of the
primitive procedures that can appear
in the expressions we will be evaluating. The
global environment also includes bindings for the symbols
true
and
false
, so that they can be used as variables in expressions
to be evaluated.
(define (setup-environment)
(let ((initial-env
(extend-environment (primitive-procedure-names)
(primitive-procedure-objects)
the-empty-environment)))
(define-variable! 'true true initial-env)
(define-variable! 'false false initial-env)
initial-env))
(define the-global-environment (setup-environment))
It does not matter how we represent the primitive procedure objects,
so long as
apply
can identify and apply them by using the
procedures
primitive-procedure?
and
apply-primitive-procedure
. We have chosen to represent a primitive
procedure as a list beginning with the symbol
primitive
and
containing a procedure in the underlying Lisp that implements that primitive.
(define (primitive-procedure? proc)
(tagged-list? proc 'primitive))
(define (primitive-implementation proc) (cadr proc))
Setup-environment
will get the primitive names and implementation
procedures from a list:
16
(define primitive-procedures
(list (list 'car car)
(list 'cdr cdr)
(list 'cons cons)
(list 'null? null?)
<
more primitives
>
))
(define (primitive-procedure-names)
(map car
primitive-procedures))
(define (primitive-procedure-objects)
(map (lambda (proc) (list 'primitive (cadr proc)))
primitive-procedures))
To apply a primitive procedure, we simply apply the implementation
procedure to the arguments, using the underlying Lisp system:
17
(define (apply-primitive-procedure proc args)
(apply-in-underlying-scheme
(primitive-implementation proc) args))
For convenience in running the metacircular evaluator, we provide a
driver loop
that models the read-eval-print loop of the underlying
Lisp system. It prints a
prompt
, reads an input expression,
evaluates this expression in the global environment, and prints the
result. We precede each printed result by an
output prompt
so
as to distinguish the value of the expression from other
output that may be printed.
18
(define input-prompt ";;; M-Eval input:")
(define output-prompt ";;; M-Eval value:")
(define (driver-loop)
(prompt-for-input input-prompt)
(let ((input (read)))
(let ((output (eval input the-global-environment)))
(announce-output output-prompt)
(user-print output)))
(driver-loop))
(define (prompt-for-input string)
(newline) (newline) (display string) (newline))
(define (announce-output string)
(newline) (display string) (newline))
We use a special printing procedure,
user-print
, to avoid printing the
environment part of a compound procedure, which may be a very long list
(or may even contain cycles).
(define (user-print object)
(if (compound-procedure? object)
(display (list 'compound-procedure
(procedure-parameters object)
(procedure-body object)
'
(display object)))
Now all we need to do to run the evaluator is to initialize the
global environment and start the driver loop. Here is a sample
interaction:
(define the-global-environment (setup-environment))
(driver-loop)
;;; M-Eval input:
(define (append x y)
(if (null? x)
y
(cons (car x)
(append (cdr x) y))))
;;; M-Eval value:
ok
;;; M-Eval input:
(append '(a b c) '(d e f))
;;; M-Eval value:
(a b c d e f)
Exercise 4.14.
Eva Lu Ator and Louis Reasoner are each experimenting with the
metacircular evaluator. Eva types in the definition of
map
, and
runs some test programs that use it. They work fine. Louis, in contrast,
has installed the system version of
map
as a primitive for the
metacircular evaluator. When he tries it, things go terribly
wrong. Explain why Louis's
map
fails even though Eva's works.
In thinking about a Lisp program that evaluates Lisp expressions, an
analogy might be helpful. One operational view of the meaning of a
program is that a
program is a description of an abstract (perhaps
infinitely large) machine. For example, consider the familiar
program to compute factorials:
(define (factorial n)
(if (= n 1)
1
(* (factorial (- n 1)) n)))
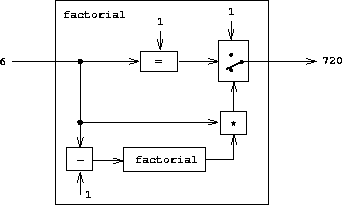
We may regard this program as the description of a machine containing
parts that decrement, multiply, and test for equality, together with a
two-position switch and another factorial machine. (The factorial
machine is infinite because it contains another factorial machine
within it.) Figure
4.2
is a flow diagram for the
factorial machine, showing how the parts are wired together.
 |
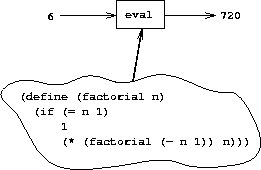
In a similar way, we can regard the evaluator as a very special
machine that takes as input a description of a machine. Given this
input, the evaluator configures itself to emulate the machine
described. For example, if we feed our evaluator the definition of
factorial
, as shown in figure
4.3
, the
evaluator will be able to compute factorials.
 |