Structure and Interpretation of Computer Programs (98 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

Cons
is performed by allocating an unused index and storing the
arguments to
cons
in
the-cars
and
the-cdrs
at that
indexed vector position. We presume that there is a special register,
free
, that always holds a pair pointer containing the next
available index, and that we can increment the index part of that
pointer to find the next free location.
11
For example, the instruction
(assign <
reg
1
> (op cons) (reg <
reg
2
>) (reg <
reg
3
>))
is implemented as the following sequence of vector
operations:
12
(perform
(op vector-set!) (reg the-cars) (reg free) (reg <
reg
2
>))
(perform
(op vector-set!) (reg the-cdrs) (reg free) (reg <
reg
3
>))
(assign <
reg
1
> (reg free))
(assign free (op +) (reg free) (const 1))
The
eq?
operation
(op eq?) (reg <
reg
1
>) (reg <
reg
2
>)
simply tests the equality of all fields in the registers, and
predicates such as
pair?
,
null?
,
symbol?
, and
number?
need only check the type field.
Although our register machines use stacks, we need do nothing special
here, since stacks can be modeled in terms of lists. The stack can be
a list of the saved values, pointed to by a special register
the-stack
. Thus,
(save <
reg
>)
can be implemented as
(assign the-stack (op cons) (reg <
reg
>) (reg the-stack))
Similarly,
(restore <
reg
>)
can be implemented as
(assign <
reg
> (op car) (reg the-stack))
(assign the-stack (op cdr) (reg the-stack))
and
(perform (op initialize-stack))
can be implemented as
(assign the-stack (const ()))
These operations can be further expanded in terms of the vector
operations given above. In conventional computer architectures,
however, it is usually advantageous to allocate the stack as a
separate vector. Then pushing and popping the stack can be
accomplished by incrementing or decrementing an index into that
vector.
Exercise 5.20.
Draw the box-and-pointer representation and the memory-vector
representation (as in figure
5.14
) of the
list structure produced by
(define x (cons 1 2))
(define y (list x x))
with the
free
pointer initially
p1
. What is the final
value of
free
? What pointers represent the values of
x
and
y
?
Exercise 5.21.
Implement register machines for the following procedures.
Assume that the list-structure memory operations are available as
machine primitives.
a. Recursive
count-leaves
:
(define (count-leaves tree)
(cond ((null? tree) 0)
((not (pair? tree)) 1)
(else (+ (count-leaves (car tree))
(count-leaves (cdr tree))))))
b. Recursive
count-leaves
with explicit counter:
(define (count-leaves tree)
(define (count-iter tree n)
(cond ((null? tree) n)
((not (pair? tree)) (+ n 1))
(else (count-iter (cdr tree)
(count-iter (car tree) n)))))
(count-iter tree 0))
Exercise 5.22.
Exercise
3.12
of section
3.3.1
presented an
append
procedure that appends two lists to form a
new list and an
append!
procedure that splices two lists
together. Design a register machine to implement each of these
procedures. Assume that the list-structure memory operations are
available as primitive operations.
The representation method outlined in
section
5.3.1
solves the problem of implementing
list structure, provided that we have an infinite amount of memory.
With a real computer we will eventually run out of free space in which
to construct new pairs.
13
However, most of the pairs generated in a typical
computation are used only to hold intermediate results. After these
results are accessed, the pairs are no longer needed – they are
garbage
. For instance, the computation
(accumulate + 0 (filter odd? (enumerate-interval 0 n)))
constructs two lists: the enumeration and the result of filtering
the enumeration. When the accumulation is complete, these lists are
no longer needed, and the allocated memory can be reclaimed. If we
can arrange to collect all the garbage periodically, and if this turns
out to recycle memory at about the same rate at which we construct new
pairs, we will have preserved the illusion that there is an infinite
amount of memory.
In order to recycle pairs, we must have a way to determine which
allocated pairs are not needed (in the sense that their contents can
no longer influence the future of the computation). The method we
shall examine for accomplishing this is known as
garbage
collection
. Garbage collection is based on the observation that, at
any moment in a Lisp interpretation, the only objects that can
affect the future of the computation are those that can be reached by
some succession of
car
and
cdr
operations starting from
the pointers that are currently in the machine registers.
14
Any memory cell
that is not so accessible may be recycled.
There are many ways to perform garbage collection. The method we
shall examine here is called
stop-and-copy
. The basic idea is
to divide memory into two halves: “working memory” and “free
memory.” When
cons
constructs pairs, it allocates these in
working memory. When working memory is full, we perform garbage
collection by locating all the useful pairs in working memory and
copying these into consecutive locations in free memory. (The useful
pairs are located by tracing all the
car
and
cdr
pointers,
starting with the machine registers.) Since we do not copy the
garbage, there will presumably be additional free memory that we can
use to allocate new pairs. In addition, nothing in the working memory
is needed, since all the useful pairs in it have been copied. Thus,
if we interchange the roles of working memory and free memory, we can
continue processing; new pairs will be allocated in the new working
memory (which was the old free memory). When this is full, we can
copy the useful pairs into the new free memory (which was the old
working memory).
15
We now use our register-machine language to describe the stop-and-copy
algorithm in more detail. We will assume that there is a register
called
root
that contains a pointer to a structure that
eventually points at all accessible data. This can be arranged by
storing the contents of all the machine registers in a
pre-allocated list pointed at by
root
just before starting
garbage collection.
16
We also assume that, in addition to the
current working memory, there is free memory available into which we
can copy the useful data. The current working memory consists of
vectors whose base addresses are in
registers called
the-cars
and
the-cdrs
, and the free memory is in registers called
new-cars
and
new-cdrs
.
Garbage collection is triggered when we exhaust the free cells in the
current working memory, that is, when a
cons
operation attempts
to increment the
free
pointer beyond the end of the memory
vector. When the garbage-collection process is complete, the
root
pointer will point into the new memory, all objects accessible
from the
root
will have been moved to the new memory, and the
free
pointer will indicate the next place in the new memory
where a new pair can be allocated. In addition, the roles of working
memory and new memory will have been interchanged – new pairs will be
constructed in the new memory, beginning at the place indicated by
free
, and the (previous) working memory will be available as the
new memory for the next garbage collection.
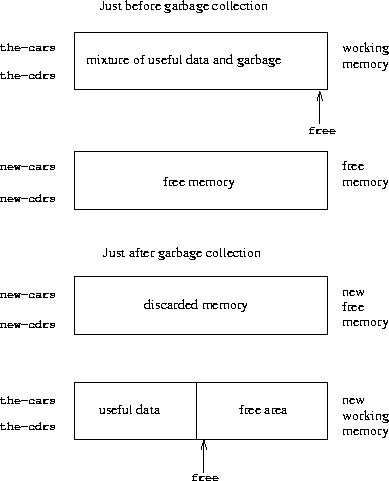
Figure
5.15
shows the arrangement of memory just
before and just after garbage collection.
 |
The state of the garbage-collection process is controlled by
maintaining two pointers:
free
and
scan
. These are
initialized to point to the beginning of the new memory. The
algorithm begins by relocating the pair pointed at by
root
to
the beginning of the new memory. The pair is copied, the
root
pointer is adjusted to point to the new location, and the
free
pointer is incremented. In addition, the old location of the pair is
marked to show that its contents have been moved. This marking is
done as follows: In the
car
position, we place a special tag
that signals that this is an already-moved object. (Such an object is
traditionally called a
broken heart
.)
17
In the
cdr
position we place a
forwarding
address
that points at the location to which the object has been
moved.
After relocating the root, the garbage collector enters its basic
cycle. At each step in the algorithm, the
scan
pointer
(initially pointing at the relocated root) points at a pair that has
been moved to the new memory but whose
car
and
cdr
pointers still refer to objects in the old memory. These objects are
each relocated, and the
scan
pointer is incremented. To
relocate an object (for example, the object indicated by the
car
pointer of the pair we are scanning) we check to see if the object has
already been moved (as indicated by the presence of a broken-heart tag
in the
car
position of the object). If the object has not
already been moved, we copy it to the place indicated by
free
,
update
free
, set up a broken heart at the object's old location,
and update the pointer to the object (in this
example, the
car
pointer of the pair we are scanning) to point
to the new location. If the object has already been moved, its
forwarding address (found in the
cdr
position of the broken
heart) is substituted for the pointer in the pair being scanned.
Eventually, all accessible objects will have been moved and scanned,
at which point the
scan
pointer will overtake the
free
pointer and the process will terminate.
We can specify the stop-and-copy algorithm as a sequence of
instructions for a register
machine. The basic step of relocating an object is accomplished by a
subroutine called
relocate-old-result-in-new
. This
subroutine gets its argument, a pointer to the object to be relocated,
from a register named
old
. It relocates the designated object
(incrementing
free
in the process),
puts a pointer to the relocated object into a register called
new
, and returns by branching to the entry point stored in the register
relocate-continue
. To begin garbage collection, we invoke this
subroutine to relocate the
root
pointer, after initializing
free
and
scan
. When the relocation of
root
has been
accomplished, we install the new pointer as the new
root
and
enter the main loop of the garbage collector.
begin-garbage-collection
(assign free (const 0))
(assign scan (const 0))
(assign old (reg root))
(assign relocate-continue (label reassign-root))
(goto (label relocate-old-result-in-new))
reassign-root
(assign root (reg new))
(goto (label gc-loop))
In the main loop of the garbage collector we must determine whether
there are any more objects to be scanned. We do this by testing
whether the
scan
pointer is coincident with the
free
pointer. If the pointers are equal, then all accessible objects have
been relocated, and we branch to
gc-flip
, which cleans things up
so that we can continue the interrupted computation. If there are
still pairs to be scanned, we call the relocate subroutine to relocate
the
car
of the next pair (by placing the
car
pointer in
old
). The
relocate-continue
register is set up so that the
subroutine will return to update the
car
pointer.