Structure and Interpretation of Computer Programs (65 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

This gives us a stream of better and better approximations to π,
although the approximations converge rather slowly. Eight terms of
the sequence bound the value of π between 3.284 and 3.017.
So far, our use of the stream of states approach is not much different
from updating state variables. But streams give us an opportunity to
do some interesting tricks. For example, we can transform a stream
with a
sequence accelerator
that converts a sequence of
approximations to a new sequence that converges to the same value as
the original, only faster.
One such accelerator, due to the eighteenth-century Swiss mathematician
Leonhard Euler, works well with sequences that are partial sums of
alternating series (series of terms with alternating signs).
In Euler's technique, if
S
n
is the
n
th term
of the original sum sequence, then the accelerated sequence has terms
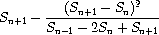
Thus, if the original sequence is represented as a stream of values,
the transformed sequence is given by
(define (euler-transform s)
(let ((s0 (stream-ref s 0))
;
S
n
-1
(s1 (stream-ref s 1))
;
S
n
(s2 (stream-ref s 2)))
;
S
n
+1
(cons-stream (- s2 (/ (square (- s2 s1))
(+ s0 (* -2 s1) s2)))
(euler-transform (stream-cdr s)))))
We can demonstrate Euler acceleration with our sequence of
approximations to π:
(display-stream (euler-transform pi-stream))
3.166666666666667
3.1333333333333337
3.1452380952380956
3.13968253968254
3.1427128427128435
3.1408813408813416
3.142071817071818
3.1412548236077655
...
Even better, we can accelerate the accelerated sequence, and
recursively accelerate that, and so on. Namely, we create a stream of
streams (a structure we'll call a
tableau
) in which each stream
is the transform of the preceding one:
(define (make-tableau transform s)
(cons-stream s
(make-tableau transform
(transform s))))
The tableau has the form

Finally, we form a sequence by taking the first term in each row of
the tableau:
(define (accelerated-sequence transform s)
(stream-map stream-car
(make-tableau transform s)))
We can demonstrate this kind of “super-acceleration” of the π
sequence:
(display-stream (accelerated-sequence euler-transform
pi-stream))
4.
3.166666666666667
3.142105263157895
3.141599357319005
3.1415927140337785
3.1415926539752927
3.1415926535911765
3.141592653589778
...
The result is impressive. Taking eight terms of the sequence yields
the correct value of π to 14 decimal places. If we had used only
the original π sequence, we would need to compute on the order of
10
13
terms (i.e., expanding the series far enough so that the
individual terms are less then 10
-13
) to get that much accuracy!
We could have implemented these acceleration techniques without
using streams. But the stream formulation is particularly elegant and
convenient because the entire sequence of states is available to us as a
data structure that can be manipulated with a uniform set of
operations.
Exercise 3.63.
Louis Reasoner asks why the
sqrt-stream
procedure was not
written in the following more straightforward way, without
the local variable
guesses
:
(define (sqrt-stream x)
(cons-stream 1.0
(stream-map (lambda (guess)
(sqrt-improve guess x))
(sqrt-stream x))))
Alyssa P. Hacker replies that this version of the procedure is
considerably less efficient because it performs redundant computation.
Explain Alyssa's answer. Would the two versions still differ in
efficiency if our implementation of
delay
used only
(lambda
() <
exp
>)
without using the optimization provided by
memo-proc
(section
3.5.1
)?
Exercise 3.64.
Write a procedure
stream-limit
that takes as arguments a stream
and a number (the tolerance). It should examine the stream until it
finds two successive elements that differ in absolute value by less
than the tolerance, and return the second of the two elements. Using
this, we could compute square roots up to a given tolerance by
(define (sqrt x tolerance)
(stream-limit (sqrt-stream x) tolerance))
Exercise 3.65.
Use the series
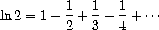
to compute three sequences of approximations to the natural logarithm of 2,
in the same way we did above for π.
How rapidly do these sequences converge?
In section
2.2.3
, we saw how the sequence paradigm
handles traditional nested loops as processes defined on sequences of
pairs. If we generalize this technique to infinite streams, then we
can write programs that are not easily represented as loops, because
the “looping” must range over an infinite set.
For example, suppose we want to generalize the
prime-sum-pairs
procedure of section
2.2.3
to produce the stream
of pairs of
all
integers (
i
,
j
) with
i
<
j
such that
i
+
j
is prime. If
int-pairs
is the sequence of all pairs of integers (
i
,
j
)
with
i
<
j
, then our required stream is simply
66
(stream-filter (lambda (pair)
(prime? (+ (car pair) (cadr pair))))
int-pairs)
Our problem, then, is to produce the stream
int-pairs
. More
generally, suppose we have two streams
S
= (
S
i
) and
T
= (
T
j
),
and imagine the infinite rectangular array
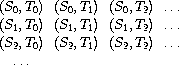
We wish to generate a stream that contains all the pairs in the array
that lie on or above the diagonal, i.e., the pairs
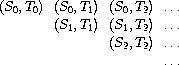
(If we take both
S
and
T
to be the stream of integers, then this
will be our desired stream
int-pairs
.)
Call the general stream of pairs
(pairs S T)
, and consider it to
be composed of three parts: the pair (
S
0
,
T
0
), the
rest of the pairs in the first row, and the remaining pairs:
67
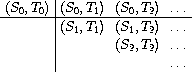
Observe that the third piece in this decomposition (pairs that are not in the
first row) is (recursively) the pairs formed from
(stream-cdr S)
and
(stream-cdr T)
. Also note that the second piece (the rest
of the first row) is
(stream-map (lambda (x) (list (stream-car s) x))
(stream-cdr t))
Thus we can form our stream of pairs as follows:
(define (pairs s t)
(cons-stream
(list (stream-car s) (stream-car t))
(<
combine-in-some-way
>
(stream-map (lambda (x) (list (stream-car s) x))
(stream-cdr t))
(pairs (stream-cdr s) (stream-cdr t)))))
In order to complete the procedure, we must choose some way to combine
the two inner streams. One idea is to use the stream analog of the
append
procedure from section
2.2.1
:
(define (stream-append s1 s2)
(if (stream-null? s1)
s2
(cons-stream (stream-car s1)
(stream-append (stream-cdr s1) s2))))