Structure and Interpretation of Computer Programs (42 page)

Because we installed the polynomial addition and
multiplication procedures
add-poly
and
mul-poly
in the generic
arithmetic system as the
add
and
mul
operations
for type
polynomial
, our system is also
automatically able to handle polynomial operations such as

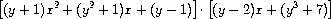
The reason is that when the system tries to combine coefficients, it
will dispatch through
add
and
mul
. Since the coefficients
are themselves polynomials (in
y
), these will be combined using
add-poly
and
mul-poly
. The result is a kind of
“data-directed
recursion” in which, for example, a call to
mul-poly
will result
in recursive calls to
mul-poly
in order to multiply the
coefficients. If the coefficients of the coefficients were themselves
polynomials (as might be used to represent polynomials in three
variables), the data direction would ensure that the system would
follow through another level of recursive calls, and so on through as
many levels as the structure of the data dictates.
⁵⁷

Finally, we must confront the job of implementing a good
representation for term lists. A term list is, in effect, a set of
coefficients keyed by the order of the term. Hence, any of the
methods for representing sets, as discussed in
section 
2.3.3
, can be applied to this task. On
the other hand, our procedures
add-terms
and
mul-terms
always
access term lists sequentially from highest to lowest order. Thus, we
will use some kind of ordered list representation.

How should we structure the list that represents a term list? One
consideration is the “density” of the polynomials we intend to
manipulate. A polynomial is said to be
dense
if it has nonzero
coefficients in terms of most orders. If it has many zero terms it
is said to be
sparse
. For example,

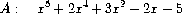
is a dense polynomial, whereas

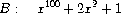
is sparse.

The term lists of dense polynomials are most efficiently represented
as lists of the coefficients. For example,
A
above would be nicely
represented as
(1 2 0 3 -2 -5)
. The order of a term in this
representation is the length of the sublist beginning with that term's
coefficient, decremented by 1.
⁵⁸
This would be a terrible representation for a
sparse polynomial such as
B
: There would be a giant list of zeros
punctuated by a few lonely nonzero terms. A more reasonable
representation of the term list of a sparse polynomial is as a list of
the nonzero terms, where each term is a list containing the order of the
term and the coefficient for that order. In such a scheme, polynomial
B
is efficiently represented as
((100 1) (2 2) (0 1))
. As
most polynomial manipulations are performed on sparse polynomials, we
will use this method. We will assume that term lists are represented
as lists of terms, arranged from highest-order to lowest-order term.
Once we have made this decision, implementing the selectors and
constructors for terms and term lists is straightforward:
⁵⁹

(define (adjoin-term term term-list)
  (if (=zero? (coeff term))
      term-list
      (cons term term-list)))
(define (the-empty-termlist) '())
(define (first-term term-list) (car term-list))
(define (rest-terms term-list) (cdr term-list))
(define (empty-termlist? term-list) (null? term-list))
(define (make-term order coeff) (list order coeff))
(define (order term) (car term))
(define (coeff term) (cadr term))

where
=zero?
is as defined in
exercise 
2.80
. (See also exercise 
2.87
below.)

Users of the polynomial package
will create (tagged) polynomials by means of the procedure:

(define (make-polynomial var terms)
  ((get 'make 'polynomial) var terms))

Exercise 2.87.
  
Install
=zero?
for polynomials in the generic arithmetic
package. This will allow
adjoin-term
to work for polynomials
with coefficients that are themselves polynomials.

Exercise 2.88.
  
Extend the polynomial system to include subtraction of polynomials.
(Hint: You may find it helpful to define a generic negation operation.)

Exercise 2.89.
  Define procedures that implement the term-list representation
described above as appropriate for dense polynomials.

Exercise 2.90.
  Suppose we want to have a polynomial system that is efficient for both
sparse and dense polynomials. One way to do this is to allow both
kinds of term-list representations in our system. The situation is
analogous to the complex-number example of section 
2.4
,
where we allowed both rectangular and polar representations.
To do this we must distinguish different types of term lists and make
the operations on term lists generic. Redesign the polynomial system
to implement this generalization. This is a major effort, not a local
change.

Exercise 2.91.
  
A univariate polynomial can be divided by another one to produce a
polynomial quotient and a polynomial remainder. For example,

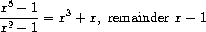
Division can be performed via long division.
That is, divide the highest-order term of the dividend by
the highest-order term of the divisor. The result is the first term of the
quotient. Next, multiply the result by the divisor, subtract that
from the dividend, and produce the rest of the answer by recursively
dividing the difference by the divisor. Stop when the order of the
divisor exceeds the order of the dividend and declare the dividend to
be the remainder. Also, if the dividend ever becomes zero, return
zero as both quotient and remainder.

We can design a
div-poly
procedure on the model of
add-poly
and
mul-poly
. The procedure checks to see if the two polys have
the same variable. If so,
div-poly
strips off the variable and
passes the problem to
div-terms
, which performs the division
operation on term lists.
Div-poly
finally reattaches the variable
to the result supplied by
div-terms
. It is convenient
to design
div-terms
to compute both the quotient and the remainder
of a division.
Div-terms
can take two term lists as arguments and
return a list of the quotient term list and the remainder term list.

Complete the following definition of
div-terms
by filling in the
missing expressions. Use this to implement
div-poly
, which takes
two polys as arguments and returns a list of the quotient and
remainder polys.

(define (div-terms L1 L2)
  (if (empty-termlist? L1)
      (list (the-empty-termlist) (the-empty-termlist))
      (let ((t1 (first-term L1))
            (t2 (first-term L2)))
        (if (> (order t2) (order t1))
            (list (the-empty-termlist) L1)
            (let ((new-c (div (coeff t1) (coeff t2)))
                  (new-o (- (order t1) (order t2))))
              (let ((rest-of-result
                     <
compute rest of result recursively
>
                     ))
                <
form complete result
>
                ))))))

Our polynomial system illustrates how objects of one type
(polynomials) may in fact be complex objects that have objects of many
different types as parts. This poses no real difficulty in defining
generic operations. We need only install appropriate generic operations
for performing the necessary manipulations of the parts of the
compound types. In fact, we saw that polynomials form a kind of
“recursive data abstraction,” in that parts of a polynomial may
themselves be polynomials. Our generic operations and our
data-directed programming style can handle this complication without
much trouble.

On the other hand, polynomial algebra is a system for which the data
types cannot be naturally arranged in a tower. For instance, it is
possible to have polynomials in
x
whose coefficients are polynomials
in
y
. It is also possible to have polynomials in
y
whose
coefficients are polynomials in
x
. Neither of these types is
“above” the other in any natural way, yet it is often necessary to
add together elements from each set. There are several ways to do
this. One possibility is to convert one polynomial to the type of the
other by expanding and rearranging terms so that both polynomials have
the same principal variable. One can impose a towerlike structure on
this by ordering the variables and thus always converting any
polynomial to a
“canonical form” with the highest-priority variable
dominant and the lower-priority variables buried in the coefficients.
This strategy works fairly well, except that the conversion may expand
a polynomial unnecessarily, making it hard to read and perhaps less
efficient to work with. The tower strategy is certainly not natural
for this domain or for any domain where the user can invent new types
dynamically using old types in various combining forms, such as
trigonometric functions, power series, and integrals.

It should not be surprising that controlling
coercion is a serious
problem in the design of large-scale algebraic-manipulation systems.
Much of the complexity of such systems is concerned with relationships
among diverse types. Indeed, it is fair to say that we do not yet
completely understand coercion. In fact, we do not yet completely
understand the concept of a data type. Nevertheless, what we know
provides us with powerful structuring and modularity principles to
support the design of large systems.