Structure and Interpretation of Computer Programs (43 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

Exercise 2.92.
By imposing an ordering on variables, extend the polynomial package so
that addition and multiplication of polynomials works for polynomials
in different variables. (This is not easy!)
We can extend our generic arithmetic system to include
rational
functions
. These are “fractions” whose numerator and denominator
are polynomials, such as
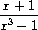
The system should be able to add, subtract, multiply, and divide
rational functions, and to perform such computations as
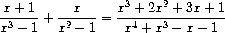
(Here the sum has been simplified by removing common factors.
Ordinary “cross multiplication” would have produced a
fourth-degree polynomial over a fifth-degree polynomial.)
If we modify our rational-arithmetic package so that it uses generic
operations, then it will do what we want, except for the problem
of reducing fractions to lowest terms.
Exercise 2.93.
Modify the rational-arithmetic package to use generic operations, but
change
make-rat
so that it does not attempt to reduce fractions
to lowest terms. Test your system by calling
make-rational
on
two polynomials to produce a rational function
(define p1 (make-polynomial 'x '((2 1)(0 1))))
(define p2 (make-polynomial 'x '((3 1)(0 1))))
(define rf (make-rational p2 p1))
Now add
rf
to itself, using
add
. You will observe that
this addition procedure does not reduce fractions to lowest terms.
We can reduce polynomial fractions to lowest terms using the same idea
we used with integers: modifying
make-rat
to divide both the
numerator and the denominator by their greatest common divisor. The
notion of
“greatest common divisor” makes sense for polynomials. In
fact, we can compute the GCD of two polynomials using essentially the
same Euclid's Algorithm that works for integers.
60
The
integer version is
(define (gcd a b)
(if (= b 0)
a
(gcd b (remainder a b))))
Using this, we could make the obvious modification to define a GCD
operation that works on term lists:
(define (gcd-terms a b)
(if (empty-termlist? b)
a
(gcd-terms b (remainder-terms a b))))
where
remainder-terms
picks out the remainder component of the
list returned by the term-list division operation
div-terms
that
was implemented in exercise
2.91
.
Exercise 2.94.
Using
div-terms
, implement the procedure
remainder-terms
and
use this to define
gcd-terms
as above. Now write a procedure
gcd-poly
that computes the polynomial GCD of two polys.
(The procedure should signal an error if the two polys are not
in the same variable.) Install in the system a generic operation
greatest-common-divisor
that reduces to
gcd-poly
for polynomials
and to ordinary
gcd
for ordinary numbers. As a test, try
(define p1 (make-polynomial 'x '((4 1) (3 -1) (2 -2) (1 2))))
(define p2 (make-polynomial 'x '((3 1) (1 -1))))
(greatest-common-divisor p1 p2)
and check your result by hand.
Exercise 2.95.
Define
P
1
,
P
2
, and
P
3
to be the polynomials
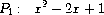
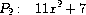
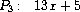
Now define
Q
1
to be the product of
P
1
and
P
2
and
Q
2
to
be the product of
P
1
and
P
3
, and use
greatest-common-divisor
(exercise
2.94
) to
compute the GCD of
Q
1
and
Q
2
.
Note that the answer is not the same as
P
1
.
This example introduces noninteger
operations into the computation, causing difficulties with the GCD
algorithm.
61
To understand what is happening,
try tracing
gcd-terms
while computing the GCD or
try performing the division by hand.
We can solve the problem exhibited in exercise
2.95
if
we use the following modification of the GCD algorithm (which really
works only in the case of polynomials with integer coefficients).
Before performing any polynomial division in the GCD computation, we
multiply the dividend by an integer constant factor, chosen to
guarantee that no fractions will arise during the division process.
Our answer will thus differ from the actual GCD by an integer constant
factor, but this does not matter in the case of reducing rational
functions to lowest terms; the GCD will be used to divide both the
numerator and denominator, so the integer constant factor will cancel
out.
More precisely, if
P
and
Q
are polynomials, let
O
1
be the
order of
P
(i.e., the order of the largest term of
P
) and let
O
2
be the order of
Q
. Let
c
be the leading coefficient of
Q
. Then it can be shown that, if we multiply
P
by the
integerizing factor
c
1+
O
1
-
O
2
, the resulting polynomial can
be divided by
Q
by using the
div-terms
algorithm without
introducing any fractions. The operation of multiplying the dividend
by this constant and then dividing is sometimes called the
pseudodivision
of
P
by
Q
. The remainder of the division is
called the
pseudoremainder
.
Exercise 2.96.
a. Implement the procedure
pseudoremainder-terms
, which is just like
remainder-terms
except that it multiplies the dividend by
the integerizing factor described above before calling
div-terms
.
Modify
gcd-terms
to use
pseudoremainder-terms
, and verify
that
greatest-common-divisor
now produces an answer with integer
coefficients on the example in exercise
2.95
.
b. The GCD now has integer coefficients, but they are larger than those
of
P
1
. Modify
gcd-terms
so that it removes common factors from
the coefficients of the answer by dividing all the coefficients by their
(integer) greatest common divisor.
Thus, here is how to reduce a rational function to lowest terms:
- Compute the GCD of the numerator and denominator, using
the version of
gcd-terms
from exercise
2.96
. - When you obtain the GCD, multiply both numerator and
denominator by the same integerizing factor before dividing through by
the GCD, so that division by the GCD will not introduce any noninteger
coefficients. As the factor you can use the leading coefficient of
the GCD raised to the power 1 +
O
1
-
O
2
, where
O
2
is the order
of the GCD and
O
1
is the maximum of the orders of the numerator
and denominator. This will ensure that dividing the numerator and
denominator by the GCD will not introduce any fractions. - The result of this operation will be a numerator and denominator
with integer coefficients. The coefficients will normally be very
large because of all of the integerizing factors, so the last step is
to remove the redundant factors by computing the (integer) greatest
common divisor of all the coefficients of the numerator and the
denominator and dividing through by this factor.
Exercise 2.97.
a. Implement this algorithm as a procedure
reduce-terms
that takes two
term lists
n
and
d
as arguments and returns a list
nn
,
dd
, which are
n
and
d
reduced to lowest terms
via the algorithm given above.
Also write a procedure
reduce-poly
, analogous to
add-poly
,
that checks to see if the two polys have
the same variable. If so,
reduce-poly
strips off the variable and
passes the problem to
reduce-terms
, then reattaches the variable
to the two term lists supplied by
reduce-terms
.
b. Define a procedure analogous to
reduce-terms
that does what the original
make-rat
did for integers:
(define (reduce-integers n d)
(let ((g (gcd n d)))
(list (/ n g) (/ d g))))
and define
reduce
as a generic operation that calls
apply-generic
to
dispatch to either
reduce-poly
(for
polynomial
arguments)
or
reduce-integers
(for
scheme-number
arguments).
You can now easily make the
rational-arithmetic package reduce fractions to lowest terms by
having
make-rat
call
reduce
before combining the given
numerator and denominator to form a rational number.
The system now
handles rational expressions in either integers or polynomials.
To test your program, try the example at the beginning of this
extended exercise: