The Bell Curve: Intelligence and Class Structure in American Life (120 page)

It may be asked if the high poverty percentage in 1939 was an artifact of the Great Depression. The numbers are inexact, but the answer is no. The poverty rate prior to the Depression—defined by the contemporary poverty line—was higher yet. (See Murray 1988b, pp. 72-73).

2
See the introduction to Part II for more on the distinction between independent and dependent variables.

3
Jensen 1980, p. 281.

4
The observed stability of tests for children up to 10 years of age is reasonably well approximated by the formula,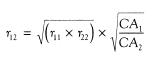
where
r
11 and
r
22 are the reliabilities of the tests on occasions 1 and 2, CA1 and CA2 are the subject’s chronological age on occasions 1 and 2, and
r
12 is the correlation between a test taken and retaken at ages CA1 and CA2. See Bloom 1964 for a full discussion.

5
After age 10, the correlation of test scores will usually fall between the product of the reliabilities of the two tests and the square root of their product. Thus, for example, the correlation of two measures of IQ after age 10 when both tests had reliabilities of .9 may be expected to fall between .81 and .9. Since the best IQ tests have reliabilities in excess of .9, this is tantamount to saying that the stability of scores is quite high. Following are some sample reliabilities as reported in the publisher’s test manuals. WISC = .95, WAIS = .97, Wonderlic Personnel Test = .95. The reliabilities of
some of the major standardized achievement tests are also extremely high. For example: ACT = .95, SAT = 90+, California Achievement Tests = .90-.95, Iowa Test of Basic Skills Composite = .98−.99. For a longer list of reliabilities and an accessible discussion of both reliability and stability, see Jensen 1980, Chap. 7.

6
Is there reason to think that, had the test been administered earlier, at age 7 or 8, the results would have turned out differently? The answer, with some reservations, is no. We would observe the normal level of fluctuation in tests administered at ages 7 and 20, with some individuals scoring higher and some lower as they grow up. The correlations between a person’s IQ obtained at age 7 and social behavior in adulthood would support the same qualitative conclusions as those based on an IQ obtained at age 20. The correlations using the younger scores would be smaller, because they measure the adult trait of intelligence less reliably than a score obtained later in life. See Appendix 3 for a discussion of changes in IQ among the members of the NLSY sample.

7
Himmelfarb 1984.

8
E.g., Ryan 1971.

9
For a few words about regression analysis, see the Introduction to Part II and Appendix 1. In fewer words still, this is a method for assessing the independent impact of each of a set of independent variables on a dependent variable. The specific form used here is called
logistic
regression analysis, the appropriate method for binary dependent variables, such as yes-no or female-male or married-unmarried.

10
We eliminate students to avoid misleading ourselves with, for example, third-year law students who have low incomes in 1989 but are soon to be making high incomes.

11
Note a distinction: Age has an important independent effect on income (income trajectories are highly sensitive to age), but not on the yes-no question of whether a person lives above the poverty line. It is also worth noting that age in the NLSY is restricted in range because the sample was all born within a few years of each other.

12
The imaginary person is sexless.

13
We refrain from precise numerical estimates of how much more important IQ is than socioeconomic background, for two reasons. First, they are not essential to the point of this discussion. Second, doing so would get us into problems of measurement and measurement error that would needlessly complicate the text. It seems sufficient for our purpose to note that IQ has a greater impact on the likelihood of being poor than socioeconomic background, as those variables are usually measured.

14
The 1991 poverty rate for persons 15 and over was 11.9 percent, compared
to 22.4 percent for children under 15. U.S. Bureau of the Census, 1992, Table 1.

15
For an analysis of the demographic reasons and some measurement issues, see Smith 1989.

16
U.S. Bureau of the Census 1992, Table C, p. xiv.

17
U.S. Bureau of the Census 1992, Table C, p. xiv.

18
Eggebeen and Lichter 1991; Smith 1989.

19
Given childless white men and women of average age, socioeconomic background, and IQ, the expected poverty rates are only 1.6 percentage points apart and are exceedingly low in both cases: 3.1 and 4.7 percent, respectively.

20
The relationships of IQ to poverty were statistically significant beyond the .01 level for both married and unmarried women. Our policy throughout the book is not routinely to report significance statistics, but at the same time not to present any relationship as being substantively significant unless we know that it also is statistically significant.

21
An entire draft of the book was written using a different measure of IQ. As described in Appendix 3, the armed forces changed the scoring system for the AFQT in 1989. The first draft was written using the old version. After discussing the merits of the old and new measures at length, we decided to switch to the new one, because, for arcane reasons, it is psychometrically superior. The substantive effects of this change on the conclusions in the book are, as far as we can tell, effectively nil. All of the analyses have also been repeated with two versions of the SES index, and many of them with three. Again, the three versions yielded substantively indistinguishable results. But each of the successive versions of the SES index was, in our judgment, a theoretically more satisfying and statistically more robust way of capturing the construct of “socioeconomic status.”

Regarding the specific analysis of the role of gender and marital status in mediating the relationship between IQ and poverty: Originally, the analysis (and the graphic included in the text on page 138) was based on married/unmarried, men/women. Then we looked more closely at women and their various marital situations, then at those marital situations for women with children. All of the poverty analyses were conducted with two measures of poverty: the official definition (represented in this book), and a definition based on cash income obtained from sources other than government transfers. We decided to present the results using the official definition to avoid an extra layer of explanation, but we have the comfort of knowing that the interpretation fits both definitions, except for a few nuances that are not important enough to warrant a place in this concise an account. We have conducted some of these analyses for age-restricted samples, to see if things change for older cohorts in ways that are not
captured by using age as an independent variable in the regression equation. Throughout all of these regression analyses, we were also looking at cross-tabulations and frequency distributions to try to see what gnomes might be lurking in the regression coefficients. Finally, we duplicated all of the analyses you see with and without sample weights, to ensure that there were no marked, mysterious differences in the two sets of results. There were undoubtedly other iterations and variations that we have forgotten over the last four years.

None of this will be surprising to our colleagues, for the process we have described is SOP for social scientists engaged in complex analyses. But for nonspecialists, the story is worth remembering. It should make you more skeptical, insofar as you understand that such enterprises are not as elegant and preordained as authors (including us) sometimes make it sound. But the story can also give you some additional confidence, insofar as, when you find yourself wondering whether we considered such-and-such an alternative way of looking at the data, the chances are fairly good that we did.

22
In passing, it just isn’t so for blacks either. The independent roles of poverty and socioeconomic status are almost exactly the same for blacks in the NLSY as for whites. See Chapter 14.

1
Kronick and Hargis 1990.

2
For a discussion of definitional issues in measuring the dropout rate, see Kominski 1990.

3
Most people get their high school degrees or equivalences later than at the age of 17, so the figure on page 144 implicitly overestimates the proportion of dropouts in the population as a whole, at least for recent times. In 1985, the U.S. Government Accounting Office estimated that 13 percent of the population between the ages of 16 and 24 could be characterized as school dropouts, which amounted to 43 million people (cited by Hahn and Lefkowitz 1987; Kronick and Hargis 1990). Dropout rates in some locales may differ markedly from the national averages. In Boston, for example, dropping out of the public schools (as distinguished from losses due to transferring out of the school system) has recently risen above 45 percent (Camayd-Freixas and Horst 1987).

4
In 1990, the percentage of persons ages 25 to 29 who had completed four years of high school or more was 85.7 percent, higher than the plotted “graduation ratio,” which is based on 17-year-olds (National Center for Education 1992, Table 8).

5
Quoted in Clignet 1974, p. 38. See Chapter 22 for additional discussion.

6
Tildsley 1936, p. 89.

7
These numbers represent an unweighted mean of the six studies of ninth graders and the nine studies of students who were either seniors or graduates. When sample sizes are taken into account, the (weighted) means for the two groups are 104.2 and 105.5 (Finch 1946, Table I, pp. 28-29). This may understate the degree of difference between the dropout and the high school senior. Other studies indicate that within any given school, a statistical relationship existed between IQ and the likelihood of finishing high school. In urban areas, the size of the correlation itself could be substantial. In one of the best such studies, Lorge found for the city of New York in the 1930s that the correlation of IQ with highest completed grade was +.66 (Lorge 1942). Some of the individual studies of specific high schools conducted during that period reviewed by Finch also showed larger differences. But those studies tended to be subject to a number of technical errors. Even giving substantial weight to them, the difference between the mean IQ of the high school dropout and youths who made it to the senior year during the 1920s was considerably less than half a standard deviation (7.5 IQ points). Perhaps children who dropped out before the ninth grade had somewhat lower IQs, so that: the overall difference between diploma holders and dropouts was larger than the difference between ninth graders and twelfth graders. The data on this issue for the first half of the century are fragmentary, however.

8
If a third dropped out between ninth grade and twelfth grade, their average IQ must have been 101, compared to 107 for the seniors and graduates; if half dropped out, it must have been 103. Assuming a population average of 100, this implies that those who dropped out prior to ninth grade had still lower scores than those who dropped out afterward.

9
Iowa State Department of Public Instruction, 1965.

10
Dillon 1949, quoted in Jensen 1980, p. 334.

11
Based on a comparison of the academic aptitude scores of the ninth graders in the sample who had and had not graduated from high school five years later. The IQ equivalents are computed from a graduate-dropout gap of 1.14 standard deviations (SDs) for boys and 1.00 SDs for girls, or approximately 1.05 SDs overall (Wise et al. 1977, Table A-3). In the late 1960s, the Youth in Transition study found a difference of about .8 SDs on the vocabulary subtest of the GATB and the Gates Reading Tests between dropouts and nondropouts, consistent with a 1 SD difference on a full-scale battery of tests (reconstructed from Table 6-1, p. 100, and Tables C-3-7 and C-3-8 in Bachman et al. 1971).

12
Looking at these numbers, some readers will be wondering how much these dropout figures represent cause and how much effect. After all, wouldn’t a person who stayed through high school and then took the IQ test have got
ten a higher score by virtue of staying in high school? This question of cause and effect may be raised with all of the topics using the NLSY, but it is most obvious for school dropout. But while age has an effect on AFQT scores and is always taken into account (either through age-equated scores in the descriptive statistics or by entering age as an independent variable in the regression analyses), there is no reason to think that presence in school is decisive. The simplest way to document this is by replicating the analyses for a restricted sample of youths who were age 16 and under when they took the test, thereby excluding almost all of the members of the sample who might create these artifacts. Having done so for all of the results reported in this chapter, we may report that it makes no difference in terms of interpretations. We will not present all of these duplicate results, but an example will illustrate.