The Bletchley Park Codebreakers (41 page)
Read The Bletchley Park Codebreakers Online
Authors: Michael Smith

*
The present author married Miss Mavis Lever on 5 November 1942
The breaking of the Enigma machine ciphers is invariably cited as the great achievement of the Bletchley Park codebreakers. But the breaking of the German enciphered teleprinter traffic, given the generic codename of ‘Fish’, was a far greater achievement. After an early break by John Tiltman, who yet again succeeded in making something extraordinarily difficult seem very easy, Bill Tutte, another of the unsung British codebreakers, broke the Lorenz SZ 40/42 teleprinter cipher attachment. The solution of this cipher machine and its traffic, codenamed ‘Tunny’ by GC&CS, must rank as one of the finest cryptanalytical achievements of all time. It also led to the development of Colossus, the world’s first semi-programmable electronic computer.
This chapter by Shaun Wylie, who worked on Tunny at Bletchley, gives a real insight into the very considerable effort devoted by GC&CS to its solution. It was more than
worthwhile, providing intelligence of the highest grade, including communications from Hitler direct to his frontline commanders during the Allied invasion of Europe. Tunny decrypts may even have helped the Russians to win the Battle of Kursk, the turning point on the Eastern Front. Stalin was distrustful of the sanitized intelligence being given to him by official British sources, but the raw Tunny decrypts passed to Moscow by John Cairncross, the ‘Fifth Man’ in the Cambridge spy ring and a member of Hut 3, gave him details of the German battle plans straight from the horse’s mouth. Not only did the Tunny decrypts provide high-grade intelligence, they provided it in unprecedented quantity. Walter Jacobs, a US Army codebreaker who worked at Bletchley Park, wrote in an official report on the operation to break Tunny that in March 1945 alone ‘upwards of five million letters of current transmission, containing intelligence of the highest order, were deciphered’.
Tunny was not the only German teleprinter cipher broken at Bletchley Park. The British codebreakers also worked on the Siemens and Halske T52 teleprinter cipher machines, codenamed ‘Sturgeon’. The T52 had at least four variants. In a little-known operation, GC&CS reconstructed them all, including the T52d, which was a significantly more complex machine than the earlier models. But for a number of reasons, including the fact that the machines were mainly used by the Luftwaffe - on which Enigma traffic already provided a great deal of information - Bletchley Park decided to concentrate on Tunny.
MS
In the autumn of 1943, I was moved from Hut 8 of Bletchley Park, where I had been working on naval Enigma, to Hut 11, where I worked on Tunny, the Lorenz SZ 40/42 teleprinter cipher machine. For me, Hut 8 had been fascinating and immediate. I was in a section, part of whose job it was to study the deciphered signals and know as much as possible about them. Suddenly what we did produced the Enigma settings and a day’s traffic tumbled out. The satisfaction to be had from the work I was involved in on Tunny was different. We formed part of a process, improving our methods of using machines and devising new approaches; actual plain-text was none of our business, only its statistical features. We were told of the importance
of the intelligence derived from Tunny, and we prided ourselves on the efficiency of our part of the operation; but the results weren’t immediate. If, however. Tunny was less exciting for me than Enigma, there was one personal bonus that more than compensated: I met and married Odette Murray, who was one of the first batch of Wrens in the section.
When the Germans invaded Russia, they started to use a new type of enciphered transmission between central headquarters and headquarters in the field. The signal was a string of teleprinter characters: each character consisted of five impulses (or ‘bits’), each impulse being either positive (a dot) or negative (a cross). These signals were taken at a station in Knockholt, near Sevenoaks in Kent, where they were painstakingly transcribed. They reached Bletchley Park on teleprinter tape and handwritten on the Red intercept forms.
All such systems were known at Bletchley Park as Fish. There were three kinds: Thrasher, Sturgeon and Tunny. Nothing positive was ever found out about Thrasher. Sturgeon (the Siemens and Halske T52 series of machines) was diagnosed after a remarkable feat of analysis by Michael Crum, an Oxford research mathematician; the system, however, was too complex for this heroic diagnosis to be followed by exploitation. Tunny, on the other hand, was both diagnosed and exploited, with a valuable harvest of intelligence. This chapter is therefore about Tunny.
In Tunny, the cipher stream (Z) is obtained from the stream of plain-text (P) by adding a stream of key (K), character by character. Symbolically Z = P + K. Two characters are added together by adding their corresponding bits level by level; two different bits add to a cross, two equal bits to a dot. So for instance (using the international teleprinter code):
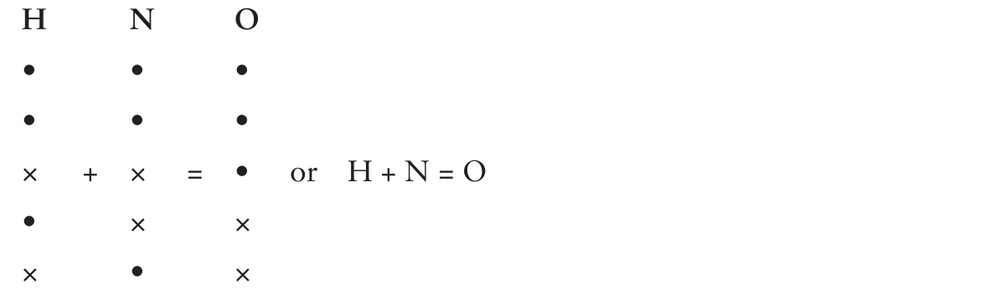
Subtraction is the same as addition (making decipherment the same process as encipherment), so that also
H = N + O and N = H + O
The key-stream in its turn was the sum of two streams:
K= χ + ψ'
The χ-stream (chi-stream) and the ψ-stream (psi-stream) were generated by twelve wheels in the Tunny machine, each with a different number of pins on its circumference, carrying its pattern of dots and crosses. The operator set the pattern by making each pin active (cross) or inactive (dot). The total number of pins on a wheel determined the length of its pseudo-random pattern.
i) Five of these, called by us the χ-wheels (chi-wheels), moved regularly, producing the chi-stream. The lengths of their patterns were 41, 31, 29, 26 and 23, the wheel of length 41 giving the χ
1
-stream for level 1 in the teleprinter code, the next for level 2, and so on up to level 5.
ii) Another five, the ψ-wheels (psi-wheels), had patterns of lengths 43, 47, 51, 53 and 59. Had they also moved regularly they would have produced a psi-stream. In fact they moved under instruction from a ‘total motor’ stream of bits; when the bit was a dot, they all stood still; when it was a cross they all moved. That produced the ‘extended’ stream ψ' (extended psi).
iii) The other two wheels were motor wheels of lengths 61 and 37; the longer μ
61
moved regularly; when it was at a cross, the shorter μ
37
moved on one place; when at a dot, μ
37
stood still. The resulting extended stream μ
37
' provided the basic motor stream of dots and crosses. In the original Tunny machine it was the basic motor that
constituted the total motor. In later versions, a ‘limitation’ stream was generated from other streams, which combined with the basic motor to give the total motor stream.
The whole contraption, remarkably, was diagnosed from the transmissions themselves.
Initially there was a single experimental communications link; later links were put into use covering continental Europe and North Africa. The German operator (assumed masculine in what follows), sitting at his teleprinter console, sent information in clear about the initial wheel settings and then switched over to the cipher mode. Whatever he then put on line was automatically enciphered by the Tunny machine and automatically deciphered at the other end. He could input messages that had already been punched onto teleprinter tape (recognized at Knockholt as such and noted as ‘Auto’ on the red forms), or he could tap out messages himself; in either case he would intersperse the messages with operator chat, doodling and corrections (all noted by Knockholt as ‘Hand’). One transmission could include many messages.
To start a new transmission, he could choose new initial wheel positions or (apparently) he could press some gadget that returned the wheels to the starting positions just used. Fortunately for us, he quite often took the easy option, sending two transmissions from the same start. Then (except when the link was using one of two particular limitations) the two transmissions had the same key-stream throughout:
Za = K + Pa and
Zb = K + Pb
So, subtracting, Za – Zb = Pa – Pb.
The observed stream Za – Zb could often be analysed by linguists as Pa – Pb, and the plain-texts of the two transmissions recovered in whole or in part. From that the key-stream can be formed as (for instance) Za – Pa. Such transmissions were said to provide a ‘depth’.
The diagnosis of Tunny was a triumph of the research section at Bletchley Park. No doubt other members of the section contributed, but the two feats are ascribed to John Tiltman and Bill Tutte. Tiltman was an already revered cryptanalyst, oozing confidence; Tutte was a recently recruited Cambridge research student, on the face of it (but only on the face of it) oozing diffidence.
Exploitation of Tunny traffic depended on three processes:
i) Diagnosis of the machine, once and for all.
ii) Recovery of wheel patterns, once for each link and pattern-period.
iii) Setting of known patterns, once for each transmission.
In early Tunny, the preamble to a transmission would include an indicator, twelve letters sent as Anton, Bertha … (A, B, etc., which were spelt out in full phonetically, to reduce garbles and errors). On 30 August 1941, two long transmissions had exactly the same indicator. A previous depth had been partly read on the correct assumption that Z = P + K. Tiltman could therefore attack this new depth on that assumption. After breaking into the beginning by reading likely starts he discovered that both transmissions were hand-sendings of the same message, but with different spacings, misspellings and corrections. This fortunate feature enabled Tiltman to battle his way through the entire depth. So different were the two texts that at the 3,976th character, when the shorter one ended, the longer still had 100 more characters.
The upshot of this was that the research section had (by subtracting the recovered plain-text from its cipher) almost 4,000 characters of key. Their only problem was what to do with it. It was months before they had a smell of a feature, and the final diagnosis did not emerge until January 1942. In what follows, the analysis is ascribed to its chief architect Tutte, although others may have made occasional contributions.
Among the multitude of things tried on this key-stream, Tutte looked at long repeats within levels. He noticed that the distances apart of these long repeats in the first level tended to be multiples of 41. Accordingly, he wrote that level out on a width of 41 so as to place many of the long repeats in the same columns. For each set of
five consecutive columns, he made a count of its five-bit characters. The distributions were significantly non-random; moreover, the distribution for one set could be matched well with that of another by adding an appropriate five-bit character throughout. These five-bit addends then turned out to fit together to give a 41-bit pattern.
This cyclic pattern was called χ
1
. He subtracted it from the first level of the key-stream to yield a stream (that would later be called ψ'
1
). It seemed to be approximately periodic and was correctly diagnosed as an extended pattern of length 43. Calling this pattern ψ
1
, the observed stream was the extended ψ'
1
.
The same method worked well on the other levels producing chipatterns (χ-patterns) of lengths 31, 29, 26 and 23 and associated psipatterns (ψ-patterns) of lengths 47, 51, 53 and 59. It then emerged that all the psi-patterns could be regarded as having moved or having stood still together, suggesting a motor stream. This was soon diagnosed as a pattern of length 37, called μ
37
, extended by a regularly moving pattern of length 61, called μ
61
. The Tiltman–Tutte triumph was complete.
This diagnosis determined all that had to be known about the Tunny machine for that pair of transmissions – its structure, the allocation of pattern-lengths to levels and the wheel patterns themselves. The research section then had to find out how long the wheel patterns stayed unchanged, and whether the allocation of lengths to levels could be changed. They had valuable help from a depth sent on 3 July 1941. They had by now (from Tiltman’s earlier success with the depth) a long sample of plaintext; with that to help them they read two stretches of lengths 500 and 300 characters of this July depth. Tutte’s method was successfully applied to the resulting stretches of key. They found that the allocation of pattern-lengths to levels was unchanged. Another depth of July 1941 was also solved. For all three depths the psi-patterns were the same; for both the July depths the chipatterns were the same, but different from those in the August depth; and the μ-patterns were all different.
