The Bletchley Park Codebreakers (43 page)

This limitation might have taken the Testery a long time to diagnose, but fortunately it was introduced in mid-March after the March patterns had been broken from a normal depth.

Among the later unbreakable depths was one 6,000 characters long. They applied Tutte’s method by hand and set the known chi-patterns and stripped them. They set the ψ's on both de-chis and compared the total motor patterns for both. Again they noted the discrepancies and found that at all of those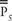
also differed. That enabled them to diagnose the limitation stream as
+
.

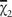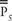Although Tutte’s method of setting known chi-wheels on a long transmission had proved successful, it took too long. In November 1942, Max Newman, an established Cambridge mathematician, was a member of the Tunny team. He pointed out that the 41×31 comparisons of Δχ
₁
+ Δχ
₂
with ΔZ
₁
+ ΔZ
₂
could be made by comparing rotating loops of punched paper tape. One would carry Z and the other, of length 41×31, would carry the 31-fold repetition of χ
₁
on one level and the 41-fold repetition of χ
₂
on another. These tapes would rotate in step, and (provided the length of the Z tape was prime to 41×31) the start of the Z-stream would eventually come opposite to all possible starts for χ
₁
and χ
₂
. Suitable photo-electrical machinery could count the number of dots in (ΔZ
₁
+ ΔZ
₂
) – (Δχ
₁
+ Δχ
₂
) between the start and the stop signs on the Z tape. Whenever the count exceeded a given threshold (or ‘set-total’), it could record the count and the number of rotations the Z tape had made. If the design was flexible enough, it could make fast counts also of other combinations and the other chi-patterns could be set in a similar way.

The scheme was approved and Newman was given the job of implementing it. His first move was to talk to engineers about the machines he needed. The most important was the machine to compare fast-moving loops of tape and to count combinations of bits. It was designed by Dr C. E. Wynn-Williams of the Telecommunications Research Establishment at Malvern and by members of Tommy Flowers’ Post Office Research Department at Dollis Hill. The first was specified in January 1943 and delivered to Bletchley Park in June 1943. Apart from Post Office racks it had two systems of adjustable pulleys, called bedsteads, around which loops of paper tape could be threaded. It looked unlikely and was christened Heath Robinson (plain Robinson to its friends).

Other machines were needed and provided. One called Tunny mimicked the German machine and could produce such things as the 41×31 long tape of χ
₁
and χ
₂
, and a great deal else. Another had five heads and could combine in various ways up to five inputs to produce four tape outputs. It was known as Mrs Miles in honour of a lady of that name who had leapt to fame by having quadruplets.

By April 1943, Newman had in his section sixteen Wrens and Donald Michie. Michie was an unprecedentedly young recruit: he had won a Classics scholarship at Oxford in the days when most of the brightest boys did Classics. He was outstandingly inventive, open-minded and vigorous, one of the heavyweights in the attack on Tunny. The Wrens were held in a typing school until June 1943 when the machines arrived. They were then divided into four watches and set about learning how to use the machines – and very good at it they became. By that time Jack Good and seven engineers had joined the section. Good came from Hut 8, where, as well as doing the standard things very well, he had helped with an influential statistical review of the material. In the Newmanry, among a mass of other contributions, he took the lead in establishing proper statistical tools for evaluating results. He once told me that he wanted to win the war by himself, and, from the way he set about Tunny, you could tell that he meant it. In the course of time other analysts like me were sent from Huts 6 and 8 and the research section; other engineers came from Dollis Hill, and other Wrens joined the original sixteen.

In the early days, the machines had teething problems and so did the analysts, but eventually the section discovered how to set all the wheels on a long enough transmission. After χ
₁
and χ
₂
had been set,
the other chi-patterns could be attacked, one by one or in pairs. They were subtracted from Z on Tunny to provide the de-chi, D = ψ' + P. Strong features of ΔP would appear in ΔD much more strongly against dots than against crosses in μ'
₃₇
where Δψ' = /. The whole length of μ'
₃₇
was run against ΔD, counting some strong feature of ΔP against dots of μ'
₃₇
. This set the motor wheels. The D stream was then ‘contracted’ by omitting the characters that came against motor dots; that gave a stream of ‘contracted’ P added to the unextended psi-stream. The psi-patterns were set by subtracting them at all settings and counting for dots (say) in levels of the contracted P-stream.

This airy description slides over the surface. Under the surface a lot was going on and a lot was going wrong. We were analysing statistical properties of samples of ΔP, and found great differences between samples. We had to identify robust features and devise efficient strategies for setting the χ’s after setting χ
₁
and χ
₂
. Our earliest efforts were often inefficient. At the places where a count exceeded its set-total threshold, the count and the number of revolutions the Z tape had made were shown on a screen and the operator wrote them down. The output of a run was a list of these. The screen, however, was quite hard to read and even the operator’s handwriting could be misread. The place on the χ
₁
χ
₂
tape that corresponded to the number of revolutions could be miscalculated; the stated length of the Z tape could be wrong. The looped tapes could stretch and they could break. It soon became clear that time spent on checking everything was time saved. Checking became an integral part of all the Newmanry routines.

Early on successes came slowly, but eventually it became clear that Robinson could indeed set known patterns in useful quantities. But new Tunny links were coming on the air, each with its own wheel-patterns; there were ten in the autumn of 1943 and eventually twenty-six; and many of them carried important strategic intelligence. Most of the long transmissions could be deciphered if only we could get at them; Robinson was overloaded and more machinery was essential.

More (and improved) Robinsons were ordered and began to arrive in late 1943. More significantly Newman consulted with Flowers about something much more powerful. Flowers had the idea of a machine in which the wheel patterns and how they affected each other could be set up on valves. The cipher text (as with Robinson) was on perforated tape that rotated on a bedstead (but much faster).
The scores and wheel-positions were typed out. In their design they went for great flexibility in the combinations that could be counted, which proved to be important. This machine, known as Colossus, was installed in February 1944. After a successful run on Robinson a new tape had to be mounted, and another often had to be made, before the next run. On Colossus you only had to change the plugging; it was liberating.

The Newmanry and the Testery had at first distinct jobs: the Testery read depths and recovered wheel-patterns; the Newmanry set transmissions on these patterns; the Testery handled the deciphering. We realized, however, in November 1943 that the Testery could set the psi- and μ-patterns on any transmission from which the chi-pattems had been correctly subtracted. We gave them the de-chi, D = P + ψ'. The Testery analysts could use the skill that enabled them to read depths to split D into its component parts, P and ψ'. It was therefore decided that the Newmanry should content itself with setting the chi-wheels and delivering the de-chis to the Testery. We would also give a character-count of ΔD, and the duty officer responsible for accepting the settings as correct would add his initials. The Testery could (and did) assign priorities, based on the look of the count and the initials that went with it. The decision meant, of course, that more transmissions could be deciphered; Robinson had formed the bottleneck, not the Testery.

About that time, the Newmanry moved from its original intimate hut into lavish accommodation in Block F near to the Testery. It housed the first Colossus, two improved Robinsons, and other improved Colossi as they arrived. The two sections formed a joint Registry, and a non-Morse section of Sixta (which was responsible for traffic analysis) was created. Its job included liaison with our suppliers, Knockholt, and with our customers, the intelligence sections. Knockholt intercepted more transmissions than Bletchley Park could decipher; Sixta, knowing both the intelligence and the cryptanalytic priorities, could get Knockholt to send us the transmission that could be used for wheel-breaking and the decipherable transmission that the customers most wanted to read.

By the start of 1944 the days of great achievements and inventions had passed. There was a lot we could and did do to improve our methods of exploitation; but for the recovery of wheel-patterns we had so far depended on depths. At about this time, however, some links began re-using autoclave limitations, and for such links depths could not be read. We needed to break the patterns from single transmissions. A method, known as rectangling, derived from one of Tutte’s hand experiments, came to our aid.

It used the Δχ
₁
+ Δχ
₂
feature that we had been using to set transmissions. If ΔZ
₁
+ ΔZ
₂
were written out on a width of 41×31, the excess of dots over crosses (positive or negative) in each column gave evidence about whether Δχ
₁
+ Δχ
₂
at those positions were equal or not. These excesses were written into a rectangle of 31 rows and 41 columns diagonally downwards, reappearing in the obvious way when they came to the bottom or the right-hand end; each row, therefore, referred to a single χ
₂
position and each column to a χ
₁
position. Any assumed pattern for Δχ
₂
, consisting of 1s for dots, –1s for crosses and 0s for ‘don’t know’ could be applied to each column to assemble a total excess for that bit of Δχ
₁
. From that a fragmentary putative pattern could be deduced for Δχ
₁
. This could, in the same way, give an excess for each bit of Δχ
₂
and so on. This process, known as crude convergence, continued until believable patterns for Δχ
₁
, and Δχ
₂
were reached. A bad start was likely to lead to a bad end, and devices were found for getting a good start with a few dots and crosses and a lot of ‘don’t knows’.

Jack Good provided significance tests. One, on the total excesses arising from the final patterns, determined whether it would be worth proceeding to the next stage. Another (too lengthy until a way was found of calculating it on Colossus) picked out the transmissions whose rectangles were likely to work.