The Bletchley Park Codebreakers (57 page)
Read The Bletchley Park Codebreakers Online
Authors: Michael Smith

RECOVERY BY DIFFERENCING
Differencing is a purely numerical method of deriving speculative additives from a column of depth. It is unaffected by whether the meanings of codegroups are known or not.
One knotty point must be got out of the way first. Japanese practice was to encipher by adding the additive to the codegroup, decipher by subtracting the additive from the enciphered group. In the cryptanalysis and in the Processing Party we followed established Washington practice of using the complement of the additive (for example, 57018 instead of 53092) instead of the additive itself. Therefore we added the complement (which we still called the additive) down a column to decipher. The reason for this was probably that cryptanalysts are always deciphering, virtually never enciphering, and that adding was less prone to error than subtracting.
As we were wholly consistent in the practice it caused no confusion. On the occasions when an additive table was captured, of course, a wholesale transformation was necessary but that never came our way. Not surprisingly, there has been some confusion between adding and subtracting in writing the history of JN-25. Throughout this Appendix I stay consistently with Japanese practice and with Appendix V: add to encipher, subtract to decipher.
Suppose that on the depth sheet we have this depth of five enciphered groups:
38898
42742
92166
18443
24236
We begin with the observation that
The difference between two enciphered groups is the same as the difference between the codegroups underlying them, because the additive which they share cancels out.
To remind, the differences here are arrived at by subtraction without carrying; that is, 27 from 45 is 28, not 18. And, given the choice of two ways round, the smaller difference is chosen; this is where differencing differs from subtraction. Here is an illustration using two groups from the middle of the above column (the additive is 68035):
| | enciphered groups | 92166 | underlying codegroups | 34131 |
| | | 18443 | | 50418 |
| | differences | 26387 | | 26387 |
Note that the codegroups scan. The differences are the same.
As inroads begin to be made into any two-stage (codebook plus additive enciphering) system, the cryptanalysts compile their lists of ‘good groups’: codegroups that have occurred, and how frequently, in the texts that have so far been deciphered. All the known good groups were sorted into numerical order, with the frequency of each, tabulated and printed as our Index of Good Groups. This was a big job done for us by the Freebornery.
Next we assembled a list of (say) our top 100 good groups by frequency of occurrence so far. Pairing each of the 100 with each of the other 99 in turn and differencing produced 4,950 differences. These again were sorted into numerical order, setting alongside each the two good groups that produced it, tabulated and printed. This was our Index of Differences, again done for us by the Freebornery. A section of it would look like this:
| | Differences in numerical order | | Good groups producing the differences | |
| | 26385 | | 58743 | 74028 |
| | 26385 | | 31314 | 57699 |
| | 26386 | | 66201 | 82587 |
| | 26387 | | 34131 | 50418 |
| | 26389 | | 04578 | 88299 |
| | 26389 | | 76833 | 92112 |
Some differences appeared more than once in the Index. Most five-digit numbers did not appear at all. Both the Index of Good Groups and the Index of Differences were regularly compiled afresh and reprinted for us as more and more good groups were identified.
Return to our depth of five enciphered groups. Pairing each of these with each of the others and differencing produces ten differences as follows:
| | Enciphered groups | Differences |
| | 38898 with 42742 | 14954 |
| | 38898 with 92166 | 46732 |
| | 38898 with 18443 | 20455 |
| | 38898 with 24236 | 14662 |
| | 42742 with 92166 | 50424 |
| | 42742 with 18443 | 34309 |
| | 42742 with 24236 | 28516 |
| | 92166 with 18443 | 26387 |
| | 34131 with 24236 | 32170 |
| | 92166 with 24236 | 16893 |
Next was the stage of looking up each of these ten differences in the Index of Differences with high hopes – often dashed! – of finding a click. Our example provides one: 26387 is there. The speculative additive is then derived by subtracting the associated good groups in the Index from their respective enciphered groups:
| | Enciphered groups | 92166 | 18443 |
| | Good groups | 34131 | 50418 |
| | Speculative additive | 68035 | 68035 |
There are three more enciphered groups in the original depth of five on which the speculative additive can now be tested, by subtracting it from each in turn to produce three more speculative codegroups:
| | Enciphered groups | 38898 | 42742 | 24236 |
| | Speculative additive | 68035 | 68035 | 68035 |
| | Speculative codegroups | 70863 | 84717 | 66201 |
All three pass the first test: they scan. This is encouraging but not decisive. There is a 1 in 27 chance that three groups will scan even if there is no underlying truth and they are just random. When checked against the Index of Good Groups their appearances are too few to be decisive. Can 68035 be recorded as the solved additive for that column or not? How we brought more precision to bear on these tricky judgements is explained in Appendix VII.
BAYES, HALL’S WEIGHTS AND THE STANDARDISING OF JUDGEMENTS
Bayes’ Theorem helps us to evaluate evidence where we have an hypothesis and a series of independent events that bear on it. We need to know for each event the probability of its happening if the hypothesis is true (call it p) and the probability of its happening if the hypothesis is false (call it q). The ratio p/q is the Bayes factor for that event.
Our state of belief before the event is expressed as the odds on the hypothesis being true: the prior odds. After the event has been taken into account, our state of belief will be expressed as the new odds on the hypothesis being true: the posterior odds. Bayes’ Theorem tells us that the posterior odds will be the prior odds multiplied by the Bayes factor.
When there are successive independent events, their factors can be multiplied together to give a composite factor subsuming all the evidence.
An example. We have a coin, and the hypothesis is that it is weighted two to one in favour of ‘heads’. The events are tosses of the coin resulting in ‘heads’ or ‘tails’. The probability of the event ‘heads’ if the hypothesis is true (p) is 2/3. If the hypothesis is false the
probability (q) is ½. The Bayes factor p/q is 4/3. By the same reasoning the Bayes factor for the event ‘tails’ is 2/3.
Our state of belief before the coin is tossed may be objective (there were known to be 3 weighted coins amongst 33 in the box that this one came from) or subjective (‘ten to one the coin’s OK, but I’m a bit suspicious’). Either of these represents prior odds of 1 to 10 on the hypothesis that the coin is weighted. Suppose 9 tosses result in 6 ‘heads’ and 3 ‘tails’. The composite Bayes factor subsuming the evidence of all 9 tosses is (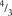 )
)
6
´ (⅔)
3
, which comes to 1.665. So the posterior odds are 1.665 times the prior odds, or 1 to 6. Our revised state of belief: ‘I’m more sceptical now, maybe more like six to one that the coin‘s OK’. Forty tosses will increase the odds to about evens (‘anybody’s guess now’) and 100 tosses to nearly 30 to 1 on the hypothesis being true (‘got to accept that it’s a wrong ‘un’).
‘Hall’s Weights’ was a procedure for placing in the right alignment to one another, or in true depth, two messages known to be enciphered on the same additive page. Marshall Hall devised it at a time when the indicator system had been broken and messages could be placed in depth immediately, but ‘just in case…’. Its time did come when the Japanese introduced bigram ordinates to specify additive starting points in December 1943.
Appendix VI noted that when messages were in true depth the non-carrying difference between two enciphered groups in depth was the same as the difference between the codegroups underlying them, because the additive they had in common cancelled out. Marshall Hall surmised that the set of differences between codegroups which both scanned would have some feature to distinguish them from differences between random groups; and was able to express that feature in terms of probabilities. With two messages placed in a speculative alignment, all the differences between respective pairs of groups were listed. He then assigned weights to those differences, probably by way of the sums (by true addition) of their digits. Combining the weights of all the differences between the two messages enabled him to estimate the probability that that speculative alignment was correct. Ian Cassels later refined the method by replacing each of the original weights by its logarithm. I do not remember the detail of assigning the weights: it is probably in the internal history ‘GC&CS Naval Cryptanalytic Studies Volume IX: The Japanese Fleet General Purpose System II’, which Ian and I wrote and which has not yet been released by GCHQ.
Return now to Appendix VI at the stage where a speculative additive (call it A) has stripped down a column of depth and produced speculative codegroups (call them P Q R…) all of which scan.
Suppose that P is a good group, recorded as having occurred 9 times amongst 5000 good groups with 7500 occurrences amongst them in the latest Index. The probability of P occurring if additive A is true (to the best estimate we have) is
9
/7500. If A is false, P is just a random scanning 5-digit number with probability 1 in 33,333. The Bayes factor for P is thus
9
/7500×33,333, which comes to 40.
Suppose that R, though it scans, is not in the Good Groups’ Index. This event must be expected to have a factor below 1 and to weigh against the truth of additive A. But the arithmetic is not straightforward, for it depends on the proportion of the codegroups that have been identified as good groups. In the early stages with only a small proportion identified, producing a speculative codegroup not in the Index is no surprise. Much later with most of the codegroups identified (if such a state was ever reached!) it would be cause for serious doubt.
My memory does not recall what analysis the party made of this question at the time. There were often occasions when a balance had to be struck between accuracy on the one hand and simplicity and speed on the other, and this was one of them. In practice the factor for a scanning group which was not a good group was taken as 1; in effect, it was disregarded. As we were in the earlier rather than the nearly-complete stage of good group identification this was probably not far wrong.
Also memory does not recall whether scanning was taken into account in calculating the composite factor for a speculative additive. At the start of the procedure it was of course decisive, as a column of speculative code groups was not taken farther unless they all (or perhaps all but one in a very deep column, to allow for a possible error in transmission or recording) scanned. But scanning had a little more to offer. The Bayes factor for the event of a group scanning was 3, so a column of 8 scanning groups could have earned a factor of 27 over one of 5 scanning groups even before the search for good groups began.
The composite Bayes factor for a speculative additive A, calculated as above, subsumed all the evidence that P, Q, R … had to offer. There was no need to agonise as to the prior odds to be assigned to the
hypothesis that the additive was correct. But the factor was neither sufficient nor infallible. A management decision was taken as to the level of threshold that should be set for a factor to have established A as correct. And the threshold could be quite sensitively adjusted with experience to get the right balance between enough confirmations to make good progress and so many as to include a lot of errors.
This application of Bayes’ Theorem took the guesswork out of testing a column of speculative codegroups, and enabled those judgements to be standardised across the whole party. The strippers in the Big Room were able, quick and accurate but not mathematically trained. The next step was to simplify the procedure for them and speed its use.
First, logarithms. When two numbers are multiplied together, their logarithms are added. By replacing each good group’s factor by its logarithm, addition replaced time-consuming multiplication in the calculation of composite factors.
Again trading a degree of accuracy for simplicity and speed, the logarithms were scaled and rounded to a series of two-digit ‘scores’. To put these quickly into the strippers’ hands the Freebornery extended the Index of Good Groups (see Appendix VI) by calculating each one’s score and listing it alongside. Adding the scores was usually a matter of mental arithmetic or at worst of pencil jotting. The thresholds were of course turned into their logarithms and scaled and rounded to match.
From this preparatory work a simple testing procedure emerged. The job was to:
- strip down a column by subtracting the speculative additive from each enciphered group in turn;
- check whether the resulting speculative codegroups all scanned;
- if they all did, look each of them up in the Index of Good Groups;
- if it was there, note its score; add the scores and
- rejoice if the total score reached the threshold, write the additive in as confirmed and move on to the next.