The Dancing Wu Li Masters (37 page)
Read The Dancing Wu Li Masters Online
Authors: Gary Zukav

The difference between experience and symbol is the difference between mythos and logos. Logos imitates, but can never replace, experience. It is a
substitute
for experience. Logos is the artificial construction of dead symbols which mimics experience on a one-to-one basis. Classical physical theory is an example of a one-to-one correspondence between theory and reality.
Einstein argued that no physical theory is complete unless every element in the real world has a definite counterpart in the theory. Einstein’s theory of relativity is the last great classical theory (even though it is a part of the new physics) because it is structured in a one-to-one way with phenomena. Unless a physical theory has one-to-one correspondence with phenomena, argued Einstein, it is not complete.
Whatever the meaning assigned to the term
complete
, the following requirement for a complete theory seems to be a necessary one:
every element of the physical reality must have a counterpart in the physical theory
.
6
[Italics in the original.]
Quantum theory does not have this one-to-one correspondence between theory and reality (it cannot predict individual events—only probabilities). According to quantum theory, individual events are chance happenings. There are no theoretical elements in quantum theory to correspond with each individual event that actually happens. Therefore quantum theory, according to Einstein, is incomplete. This was a basic issue of the famous Bohr-Einstein debates.
Mythos points toward experience, but it does not replace experience. Mythos is the opposite of intellectualism. Ceremonial chants at primitive rituals (like football games) are good examples of mythos. They endow experience with value, originality, and vitality, but they do not seek to replace it.
Theologically speaking, logos is the original sin, the eating of the fruit of knowledge, the expulsion from the Garden of Eden. Historically speaking, logos is the growth of the literary revolution, the birth of the written tradition out of the oral tradition. From any point of view, logos (literally) is a dead letter. “Knowledge,” wrote e. e. cummings, “is a polite word for / dead but not buried imagination.” He was talking about logos.
Our problem, according to Finkelstein, is that we cannot understand subatomic phenomena,
or any other kind of experience
, through the use of symbols alone. As Heisenberg observed:
The concepts initially formed by abstraction from particular situations or experiential complexes acquire a
life of their own
.
7
[Italics added].
Getting lost in the interaction of symbols is analogous to mistaking the shadows on the wall of the cave for the real world outside the cave (which is direct experience). The answer to this predicament is to approach subatomic phenomena, as well as experience in general, with a language of mythos rather than a language of logos.
Finkelstein put it this way:
If you want to envision a quantum as a dot then you are trapped. You are modeling it with classical logic. The whole point is that there
is no
classical representation for it. We have to learn to live with the experience.
Question: How do you communicate the experience?
Answer: You don’t. But by telling how you make quanta and how you measure them, you enable others to have it.
8
According to Finkelstein, a language of mythos, a language which alludes to experience but does not attempt to replace it or to mold our perception of it is the true language of physics. This is because not only the language that we use to communicate our daily experience, but also mathematics, follows a certain set of rules (classical logic).
Experience itself is not bound by these rules
. Experience follows a much more permissive set of rules (quantum logic). Quantum logic is not only more exciting than classical logic, it is more real. It is based not upon the way that we
think
of things, but upon the way that we
experience
them.
When we try to describe experience with classical logic (which is what we have been doing since we learned to write), we put on a set of blinders, so to speak, which not only restricts our field of vision, but also distorts it. These blinders are the set of rules known as classical logic. The rules of classical logic are well defined. They are simple. The only problem is that they do not correspond to experience.
The most important difference between the rules of classical logic and the rules of quantum logic involves the law of distributivity. The law of distributivity, or the distributive law, says that “A, and B or C” is the same as “A and B, or A and C.” In other words, “I flip a coin and it comes up heads or tails” has the same meaning as “I flip a coin and it comes up heads, or I flip a coin and it comes up tails.” The distributive law, which is a foundation of classical logic,
does not apply to quantum logic
. This is one of the most important but least understood aspects of von Neumann’s work. In 1936, von Neumann and his colleague, Garrett Birkhoff, published a paper which laid the foundations of quantum logic.
9
In it they used an example of a familiar (to physicists) phenomenon to disprove the distributive law. By so doing they demonstrated mathematically that it is impossible to describe experience (including subatomic phenomena) with classical logic, because the real world follows different rules. The rules that experience follows they called
quantum logic. The rules which symbols follow they called classical logic.
Finkelstein uses a version of Birkhoff and von Neumann’s example to disprove the law of distributivity. Finkelstein’s demonstration requires only three pieces of plastic. These three pieces of plastic are contained in the envelope attached to the back cover of this book. Remove them from their envelope now and examine them.
*
Notice that they are transparent and tinted about the color of sunglasses. In fact, pieces of plastic just like these but thicker
are
used for sunglasses. They are very effective in reducing glare because of their particular characteristics. These pieces of plastic are called polarizers and, of course, the sunglasses which use them are called polaroid sunglasses.
Polarizers are a special kind of light filter. Most frequently they are made of stretched sheets of plastic material in which all the molecules are elongated and aligned in the same direction. Under magnification the molecules look something like this.

These long, slender molecules are responsible for the polarization of the light which passes through them.
The polarization of light can be understood most easily as a wave phenomenon. Light waves from an ordinary light source, like the sun, emanate in every fashion, vertically, horizontally, and every way in between. This does not mean only that light radiates from a source in all directions. It means that in any given beam of light some of the light waves are vertical, some of the light waves are horizontal, some are diagonal, and so forth. To a light wave, a polarizer looks something like a picket fence. Whether it can get through the fence or not depends upon whether it is aligned with the fence or not. If the polarizer is aligned vertically, only the vertical light waves make it through. All of the other light waves are obstructed. All of the light waves that pass through a vertical polarizer are aligned vertically. This light is called vertically polarized light.
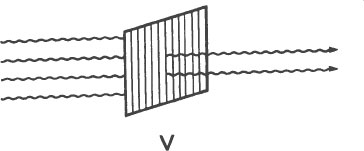
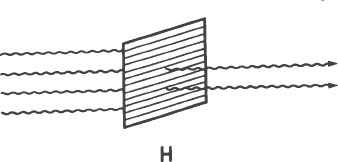
If the polarizer is aligned horizontally, only the horizontal light waves make it through. All of the other light waves are obstructed (first illustration, next page). All of the light waves that pass through a horizontal polarizer are aligned horizontally. This light is called horizontally polarized light.
No matter how the polarizer is aligned, all of the light waves passing through it are aligned in the same plane. The arrows on the polarizers indicate the direction in which the light passing through them is polarized (which way the molecules in the plastic are elongated).
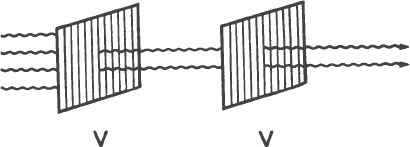
Take one of the polarizers and hold it with the arrow pointing up (or down). The light coming through this polarizer now is polarized vertically. Now take another polarizer and hold it behind the first polarizer with its arrow also pointing up (or down). Notice that, except for a slight attenuation due to the tint, all of the light that gets through the first polarizer also gets through the second polarizer.
Now rotate one of the polarizers from vertical to horizontal. As it is rotated, notice that less and less light gets through the pair. When one of the polarizers is vertical and the other polarizer is horizontal, no light gets through them at all. The first polarizer eliminates all but the horizontally polarized light waves. They are eliminated by the second polarizer, which passes only vertically polarized light. The result is that
no
light passes both the vertical and the horizontal polarizer. It does not matter whether the first polarizer is vertical and the second polarizer is horizontal or the other way round. The order of the filters is not important. In either case, no light passes through them.
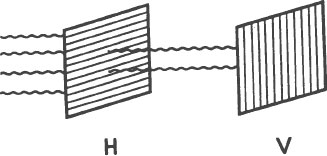
Whenever two polarizers are oriented at right angles to each other they block all light. No matter how the pair is twisted or turned as a unit, as long as they remain at right angles to each other, no light passes through them.