The Dancing Wu Li Masters (41 page)
Read The Dancing Wu Li Masters Online
Authors: Gary Zukav

Now suppose that area A and area B are very far apart. It will take a certain amount of time for a light signal to travel from area A to area B. If area A and area B are so far apart that there is insufficient time for a light signal to connect an event that happens in area A with an event that happens in area B, there is no way, according to the usual ideas in physics, that the event in area B can know about the event in area A. Physicists call this a “space-like” separation. (One event is space-like separated from another event if there is insufficient time for a light signal to connect them.) Communication between space-like separated events defies one of the most basic assumptions of physics. Yet this is exactly what the Einstein-Podolsky-Rosen thought experiment seems to illustrate. Even though they are space-like separated, the state of the particle in area B depends upon what the observer in area A decides to observe (which way he orients his magnetic field).
In other words, the Einstein-Podolsky-Rosen effect indicates that information can be communicated at
superluminal
(faster than light) speeds contrary to the accepted ideas of physicists. If the two particles in the Einstein-Podolsky-Rosen thought experiment some
how are connected by a signal, that signal is traveling faster than the speed of light. Einstein, Podolsky, and Rosen may have created the first scientific example of a superluminal connection.
Einstein himself denied this conclusion. It is not possible, he argued, that the setting we choose for a measuring device here can affect what happens somewhere else. In his autobiography, written eleven years after the Einstein-Podolsky-Rosen paper, he wrote:
…on one supposition we should, in my opinion, absolutely hold fast; the real factual situation of the system S
2
[the particle in area B] is independent of what is done with the system S
1
[the particle in area A], which is spatially separated from the former.
4
This opinion is, in effect, the principle of local causes. The principle of local causes says that what happens in one area does not depend upon variables subject to the control of an experimenter in a distant space-like separated area. The principle of local causes is common sense. The results of an experiment in a place distant and space-like separated from us should not depend on what we decide to do or not to do right here. (Except for the mother who rose in alarm at the same instant that her daughter’s distant automobile crashed into a tree—and similar cases—the macroscopic world appears to be made of local phenomena.)
Since phenomena are local in nature, argued Einstein, quantum theory has a serious flaw. According to quantum theory, changing the measuring device in area A changes the wave function which describes the particle in area B, but (according to Einstein) it cannot change “the real factual situation of the system S
2
[which] is independent of what is done with the system S
1
…”
Therefore, one and the same “factual situation” in area B has two wave functions, one for each position of the measuring device in area A. This is a flaw since it is “impossible that two different types of wave functions could be coordinated with the identical factual situation of S
2
.”
5
Here is another way of looking at the same situation: Since the
real factual situation in area B is independent of what is done in area A, there must exist
simultaneously
in area B a definite spin
up
or
down
and a definite spin
right
or
left
to account for all the results that we can get by orienting the Stern-Gerlach device in area A either vertically or horizontally. Quantum theory is not able to describe such a state in area B and, therefore, it is an incomplete theory.
*
However, Einstein closed his argument with an incredible aside:
One can escape from this conclusion [that quantum theory is incomplete] only by either assuming that the measurement of S
1
((telepathically)) changes the real situation of S
2
or by denying independent real situations as such to things which are spatially separated from each other. Both alternatives appear to me entirely unacceptable.
6
Although these alternatives were unacceptable to Einstein, they are being considered by physicists today. Few physicists believe in telepathy, but some physicists do believe either that at a deep and fundamental level there is no such thing as “independent real situations” of things which have interacted in the past but which are spa
tially separated from each other, or that changing the measuring device in area A
does
change “the real factual situation” in area B.
This brings us to Bell’s theorem.
Bell’s theorem is a mathematical proof. What it “proves” is that if the statistical predictions of quantum theory are correct, then some of our commonsense ideas about the world are profoundly mistaken.
Bell’s theorem does not demonstrate clearly in what way our commonsense ideas about the world are inadequate. There are several possibilities. Each possibility has champions among the small number of physicists who are familiar with Bell’s theorem. No matter which of the implications of Bell’s theorem we favor, however, Bell’s theorem itself leads to the inescapable conclusion that if the statistical predictions of quantum theory are correct, then our commonsense ideas about the world are profoundly deficient.
This is quite a conclusion because
the statistical predictions of quantum mechanics are always correct
. Quantum mechanics is
the
theory. It has explained everything from subatomic particles to transistors to stellar energy. It never has failed. It has no competition.
Quantum physicists realized in the 1920s that our commonsense ideas were inadequate for describing subatomic phenomena. Bell’s theorem shows that commonsense ideas are inadequate even to describe macroscopic events, events of the everyday world!
As Henry Stapp wrote:
The important thing about Bell’s theorem is that it puts the dilemma posed by quantum phenomena clearly into the realm of macroscopic phenomena…[it] shows that our ordinary ideas about the world are somehow profoundly deficient even on the macroscopic level.
7
Bell’s theorem has been reformulated in several ways since Bell published the original version in 1964. No matter how it is formu
lated, it projects the “irrational” aspects of subatomic phenomena squarely into the macroscopic domain. It says that not only do events in the realm of the very small behave in ways which are utterly different from our commonsense view of the world, but also that events in the world at large, the world of freeways and sports cars, behave in ways which are utterly different from our commonsense view of them. This incredible statement cannot be dismissed as fantasy because it is based upon the awesome and proven accuracy of the quantum theory itself.
Bell’s theorem is based upon correlations between paired particles similar to the pair of hypothetical particles in the Einstein-Podolsky-Rosen thought experiment.
*
For example, imagine a gas that emits light when it is electrically excited (think of a neon sign). The excited atoms in the gas emit photons in pairs. The photons in each pair fly off in opposite directions. Except for the difference in their direction of travel, the photons in each pair are identical twins. If one of them is polarized vertically, the other one also is polarized vertically. If one of the photons in the pair is polarized horizontally, the other photon also is polarized horizontally. No matter what the angle of polarization, both photons in every pair are polarized in the same plane.
Therefore, if we know the state of polarization of one of the particles, we automatically know the state of polarization of the other particle. This situation is similar to the situation in the Einstein-Podolsky-Rosen thought experiment, except that now we are discussing states of polarization instead of spin states.
We can verify that both photons in each pair of photons are polarized in the same plane by actually sending them through polarizers. On the next page is a picture of this (conceptually) simple procedure.
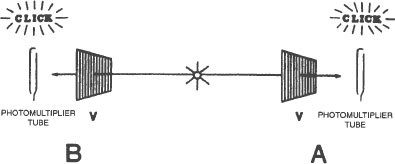
A light source in the center of the picture emits a pair of photons. On each side of the light source a polarizer is placed in the path of the emitted photon. Behind the polarizers are photomultiplier tubes which emit a click (or an audible electronic equivalent) whenever they detect a photon.
Whenever the photomultiplier tube in area A emits a click, the photomultiplier tube in area B also emits a click. This is because both of the photons in each photon pair always are polarized in the same plane, and both of the polarizers in this arrangement are aligned in the same direction (in this case, vertically). There is no theory involved here, just a matter of counting clicks. We know, and can verify, that when the polarizers both are aligned in the same direction, the photomultiplier tubes behind them will click an equal number of times. The clicks in area A are correlated with the clicks in area B. The correlation, in this case, is
one
. Whenever one of the photomultiplier tube clicks, the other photomultiplier tube always clicks as well.
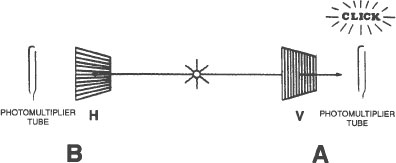
Now suppose that we orient one of the polarizers at 90 degrees to the other. On the next page is a picture of this arrangement. One of the polarizers still is aligned vertically, but the other polarizer now is aligned horizontally. Light waves that pass through a vertical polarizer are stopped by a horizontal polarizer and the other way round. Therefore, when the polarizers are oriented at right angles to each other, a click in area A
never
will be accompanied by a click in area B. The clicks in area A, again, are correlated with the clicks in area B. This time, however, the correlation is
zero
. Whenever one of the photomultiplier tubes clicks, the other photomultiplier tube
never
clicks.
There also are correlations between the clicks in area A and the clicks in area B for every other possible combination of polarizer settings between these two extremes. These statistical correlations can be predicted by the quantum theory. For a given setting of the polarizers, a certain number of clicks in one area will be accompanied by a certain number of clicks in the other area.
Bell discovered that no matter what the settings of the polarizers, the clicks in area A are correlated too strongly to the number of clicks in area B to be explained by chance. They have to be connected somehow. However, if they are connected, then the principle of local causes (which says that what happens in one area does not depend upon variables subject to the control of an experimenter in a distant space-like area) is an illusion! In short, Bell’s theorem shows that the principle of local causes, however reasonable it sounds, is mathematically incompatible with the assumption that the statistical predictions of quantum theory are valid (at least valid in this experiment and in the Einstein-Podolsky-Rosen experiment).
*
The correlations which Bell used were calculated, but untested predictions of the quantum theory. In 1964, this experiment was still a hypothetical construct. In 1972, John Clauser and Stuart Freedman at the Lawrence Berkeley Laboratory actually performed this experiment to confirm or disprove these predictions.
8
They found that the statistical predictions upon which Bell based his theorem
are
correct.
Bell’s theorem not only suggests that the world is quite different than it seems, it
demands
it. There is no question about it. Something very exciting is happening. Physicists have “proved,” rationally, that our rational ideas about the world in which we live are profoundly deficient.
In 1975, Henry Stapp, in a work supported by the U.S. Energy Research and Development Administration, wrote:
Bell’s theorem is the most profound discovery of science.
9
The deduction of superluminal communication from the results of the Clauser-Freedman experiment rests upon an important assumption: namely, that the states of the measuring devices prior to the arrival of the photons in area A and area B do not matter. This is, after all, a reasonable assumption. Normally we say that the orientation of a measuring device prior to a measurement is not relevant to the result
that we get at the time of a measurement. The result of an experiment depends upon the state of the measuring device at the time that the particle is detected by it, and not on the state of the measuring device before the particle gets there. However, superluminal communication cannot be deduced from the results of the Clauser-Freedman experiment without this assumption. Even though the photons in the photon pair cannot exchange information via light signals while they are in flight (each is traveling away from the other at the speed of light), the measuring device in area A and the measuring device in area B, which are set prior to the beginning of the experiment, may have exchanged information in the conventional manner (via light signals propagating within space-time). In other words, in the Clauser-Freedman experiment the information about the setting of the measuring device in either region has sufficient time, traveling at the speed of light or less, to reach the other region before the particle arrives.