The Goal: A Process of Ongoing Improvement (13 page)
Read The Goal: A Process of Ongoing Improvement Online
Authors: Eliyahu Goldratt

So I’ve got limits on how fast I can go—both my own (I can only go so fast for so long before I fall over and pant to death) and those of the others on the hike. However, there is no limit on my ability to slow down. Or on anyone else’s ability to slow down. Or stop. And if any of us did, the line would extend indefinitely.
What’s happening isn’t an averaging out of the fluctuations in our various speeds, but an
accumulation
of the fluctuations. And mostly it’s an accumulation of slowness
—because dependency limits the opportunities for higher fluctuations.
And that’s why the line is spreading. We can make the line shrink only by having everyone in the back of the line move much faster than Ron’s average over some distance.
Looking ahead, I can see that how much distance each of us has to make up tends to be a matter of where we are in the line. Davey only has to make up for his own slower than average fluctuations relative to Ron—that twenty feet or so which is the gap in front of him. But for Herbie to keep the length of the line from growing, he would have to make up for his own fluctuations plus those of all the kids in front of him. And here I am at the end of the line. To make the total length of the line contract, I have to move faster than average for a distance equal to all the excess space between all the boys. I have to make up for the accumulation of all their slowness.
Then I start to wonder what this could mean to me on the job. In the plant, we’ve definitely got both dependent events and statistical fluctuations. And here on the trail we’ve got both of them. What if I were to say that this troop of boys is analogous to a manufacturing system . . . sort of a model. In fact, the troop does produce a product; we produce "walk trail.’’ Ron begins production by consuming the unwalked trail before him, which is the equivalent of raw materials. So Ron processes the trail first by walking over it, then Davey has to process it next, followed by the boy behind him, and so on back to Herbie and the others and on to me.
Each of us is like an operation which has to be performed to produce a product in the plant; each of us is one of a set of dependent events. Does it matter what order we’re in? Well, somebody has to be first and somebody else has to be last. So we have dependent events no matter if we switch the order of the boys.
I’m the last operation. Only after I have walked the trail is the product "sold,’’ so to speak. And that would have to be our throughput—not the rate at which Ron walks the trail, but the rate at which I do.
What about the amount of trail between Ron and me? It has to be inventory. Ron is consuming raw materials, so the trail the rest of us are walking is inventory until it passes behind me.
And what is operational expense? It’s whatever lets us turn inventory into throughput, which in our case would be the energy the boys need to walk. I can’t really quantify that for the model, except that I know when I’m getting tired.
If the distance between Ron and me is expanding, it can only mean that inventory is increasing. Throughput is my rate of walking. Which is influenced by the fluctuating rates of the others. Hmmm. So as the slower than average fluctuations accumulate, they work their way back to me. Which means I have to slow down. Which means that, relative to the growth of inventory, throughput for the entire system goes down.
And operational expense? I’m not sure. For UniCo, whenever inventory goes up, carrying costs on the inventory go up as well. Carrying costs are a part of operational expense, so that measurement also must be going up. In terms of the hike, operational expense is increasing any time we hurry to catch up, because we expend more energy than we otherwise would.
Inventory is going up. Throughput is going down. And operational expense is probably increasing.
Is that what’s happening in my plant?
Yes, I think it is.
Just then, I look up and see that I’m nearly running into the kid in front of me.
Ah ha! Okay! Here’s proof I must have overlooked something in the analogy. The line in front of me is contracting rather than expanding. Everything must be averaging out after all. I’m going to lean to the side and see Ron walking his average twomile-an-hour pace.
But Ron is not walking the average pace. He’s standing still at the edge of the trail.
"How come we’re stopping?’’
He says, "Time for lunch, Mr. Rogo.’’
"But we’re not supposed to be having lunch here,’’ says one of the kids. "We’re not supposed to eat until we’re farther down the trail, when we reach the Rampage River.’’
"According to the schedule the troopmaster gave us, we’re supposed to eat lunch at 12:00 noon,’’ says Ron.
"And it is now 12:00 noon,’’ Herbie says, pointing to his watch. "So we have to eat lunch.’’
"But we’re supposed to be at Rampage River by now and we’re not.’’
"Who cares?’’ says Ron. "This is a great spot for lunch. Look around.’’
Ron has a point. The trail is taking us through a park, and it so happens that we’re passing through a picnic area. There are tables, a water pump, garbage cans, barbecue grills—all the necessities. (This is my kind of wilderness I’ll have you know.)
"Okay,’’ I say. "Let’s just take a vote to see who wants to eat now. Anyone who’s hungry, raise your hand.’’
Everyone raises his hand; it’s unanimous. We stop for lunch.
I sit down at one of the tables and ponder a few thoughts as I eat a sandwich. What’s bothering me now is that, first of all, there is no real way I could operate a manufacturing plant without having dependent events and statistical fluctuations. I can’t get away from that combination. But there must be a way to overcome the effects. I mean, obviously, we’d all go out of business if inventory was always increasing, and throughput was always decreasing.
What if I had a balanced plant, the kind that Jonah was saying managers are constantly trying to achieve, a plant with every resource exactly equal in capacity to demand from the market? In fact, couldn’t that be the answer to the problem? If I could get capacity perfectly balanced with demand, wouldn’t my excess inventory go away? Wouldn’t my shortages of certain parts disappear? And, anyway, how could Jonah be right and everybody else be wrong? Managers have always trimmed capacity to cut costs and increase profits; that’s the game.
I’m beginning to think maybe this hiking model has thrown me off. I mean, sure, it shows me the effect of statistical fluctuations and dependent events in combination. But is it a balanced system? Let’s say the demand on us is to walk two miles every hour—no more, no less. Could I adjust the capacity of each kid so he would be able to walk two miles per hour and no faster? If I could, I’d simply keep everyone moving constantly at the pace he should go—by yelling, whip-cracking, money, whatever—and everything would be perfectly balanced.
The problem is how can I realistically trim the capacity of fifteen kids? Maybe I could tie each one’s ankles with pieces of rope so that each would only take the same size step. But that’s a little kinky. Or maybe I could clone myself fifteen times so I have a troop of Alex Rogos with exactly the same trail-walking capacity. But that isn’t practical until we get some advancements in
cloning
technology. Or maybe I could set up some other kind of model, a more controllable one, to let me see beyond any doubt what goes on.
I’m puzzling over how to do this when I notice a kid sitting at one of the other tables, rolling a pair of dice. I guess he’s practicing for his next trip to Vegas or something. I don’t mind—although I’m sure he won’t get any merit badges for shooting craps —but the dice give me an idea. I get up and go over to him.
"Say, mind if I borrow those for a while?’’ I ask.
The kid shrugs, then hands them over.
I go back to the table again and roll the dice a couple of times. Yes, indeed: statistical fluctuations. Every time I roll the dice, I get a random number that is predictable only within a certain range, specifically numbers one to six on each die. Now what I need next for the model is a set of dependent events.
After scavenging around for a minute or two, I find a box of match sticks (the strike-anywhere kind), and some bowls from the aluminum mess kit. I set the bowls in a line along the length of the table and put the matches at one end. And this gives me a model of a perfectly balanced system.
While I’m setting this up and figuring out how to operate the model, Dave wanders over with a friend of his. They stand by the table and watch me roll the die and move matches around.
"What are you doing?’’ asks Dave.
"Well, I’m sort of inventing a game,’’ I say.
"A game? Really?’’ says his friend. "Can we play it, Mr. Rogo?’’
Why not?
"Sure you can,’’ I say.
All of a sudden Dave is interested.
"Hey, can I play too?’’ he asks.
"Yeah, I guess I’ll let you in,’’ I tell him. "In fact, why don’t you round up a couple more of the guys to help us do this.’’
While they go get the others, I figure out the details. The system I’ve set up is intended to "process’’ matches. It does this by moving a quantity of match sticks out of their box, and through each of the bowls in succession. The dice determine how many matches can be moved from one bowl to the next. The dice represent the capacity of each resource, each bowl; the set of bowls are my dependent events, my stages of production. Each has exactly the same capacity as the others, but its actual yield will fluctuate somewhat.
In order to keep those fluctuations minimal, however, I decide to use only one of the dice. This allows the fluctuations to range from one to six. So from the first bowl, I can move to the next bowls in line any quantity of matches ranging from a minimum of one to a maximum of six.
Throughput in this system is the speed at which matches come out of the last bowl. Inventory consists of the total number of matches in all of the bowls at any time. And I’m going to assume that market demand is exactly equal to the average number of matches that the system can process. Production capacity of each resource and market demand are perfectly in balance. So that means I now have a model of a perfectly balanced manufacturing plant.
Five of the boys decide to play. Besides Dave, there are Andy, Ben, Chuck, and Evan. Each of them sits behind one of the bowls. I find some paper and a pencil to record what happens. Then I explain what they’re supposed to do.
"The idea is to move as many matches as you can from your bowl to the bowl on your right. When it’s your turn, you roll the die, and the number that comes up is the number of matches you can move. Got it?’’
They all nod. "But you can only move as many matches as you’ve got in your bowl. So if you roll a five and you only have two matches in your bowl, then you can only move two matches. And if it comes to your turn and you don’t have any matches, then naturally you can’t move any.’’
They nod again.
"How many matches do you think we can move through the line each time we go through the cycle?’’ I ask them.
Perplexity descends over their faces.
"Well, if you’re able to move a maximum of six and a minimum of one when it’s your turn, what’s the average number you ought to be moving?’’ I ask them.
"Three,’’ says Andy.
"No, it won’t be three,’’ I tell them. "The mid-point between one and six isn’t three.’’
I draw some numbers on my paper.
"Here, look,’’ I say, and I show them this:
123456
And I explain that 3.5 is really the average of those six numbers.
"So how many matches do you think each of you should have moved on the average after we’ve gone through the cycle a number of times?’’ I ask.
"Three and a half per turn,’’ says Andy.
"And after ten cycles?’’
"Thirty-five,’’ says Chuck.
"And after twenty cycles?’’
"Seventy,’’ says Ben.
"Okay, let’s see if we can do it,’’ I say.
Then I hear a long sigh from the end of the table. Evan looks at me.
"Would you mind if I don’t play this game, Mr. Rogo?’’ he asks.
"How come?’’
"Cause I think it’s going to be kind of boring,’’ he says.
"Yeah,’’ says Chuck. "Just moving matches around. Like who cares, you know?’’
"I think I’d rather go tie some knots,’’ says Evan.
"Tell you what,’’ I say. "Just to make it more interesting, we’ll have a reward. Let’s say that everybody has a quota of 3.5 matches per turn. Anybody who does better than that, who averages more than 3.5 matches, doesn’t have to wash any dishes tonight. But anybody who averages less than 3.5 per turn, has to do extra dishes after dinner.’’
"Yeah, all right!’’ says Evan.
"You got it!’’ says Dave.
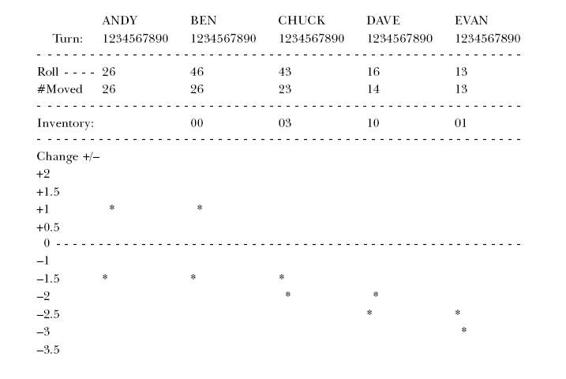
They’re all excited now. They’re practicing rolling the die. Meanwhile, I set up a grid on a sheet of paper. What I plan to do is record the amount that each of them deviates from the average. They all start at zero. If the roll of the die is a 4, 5, or 6 then I’ll record—respectively—a gain of .5, 1.5, or 2.5. And if the roll is a 1, 2, or 3 then I’ll record a loss of −2.5, −1.5, or −.5 respectively. The deviations, of course, have to be cumulative; if someone is 2.5 above, for example, his starting point on the next turn is 2.5, not zero. That’s the way it would happen in the plant.
"Okay, everybody ready?’’ I ask.
"All set.’’
I give the die to Andy.
He rolls a two. So he takes two matches from the box and puts them in Ben’s bowl. By rolling a two, Andy is down 1.5 from his quota of 3.5 and I note the deviation on the chart.
Ben rolls next and the die comes up as a four.
"Hey, Andy,’’ he says. "I need a couple more matches.’’
"No, no, no, no,’’ I say. "The game does not work that way. You can only pass the matches that are in your bowl.’’
"But I’ve only got two,’’ says Ben.
"Then you can only pass two.’’
"Oh,’’ says Ben.
And he passes his two matches to Chuck. I record a deviation of −1.5 for him too.
Chuck rolls next. He gets a five. But, again, there are only two matches he can move.
"Hey, this isn’t fair!’’ says Chuck.
"Sure it is,’’ I tell him. "The name of the game is to move matches. If both Andy and Ben had rolled five’s, you’d have five matches to pass. But they didn’t. So you don’t.’’ Chuck gives a dirty look to Andy.
"Next time, roll a bigger number,’’ Chuck says.
"Hey, what could I do!’’ says Andy.
"Don’t worry,’’ Ben says confidently. "We’ll catch up.’’
Chuck passes his measly two matches down to Dave, and I record a deviation of −1.5 for Chuck as well. We watch as Dave rolls the die. His roll is only a one. So he passes one match down to Evan. Then Evan also rolls a one. He takes the one match out of his bowl and puts it on the end of the table. For both Dave and Evan, I write a deviation of −2.5.
"Okay, let’s see if we can do better next time,’’ I say.
Andy shakes the die in his hand for what seems like an hour. Everyone is yelling at him to roll. The die goes spinning onto the table. We all look. It’s a six.
"All right!’’
"Way to go, Andy!’’
He takes six match sticks out of the box and hands them to Ben. I record a gain of +2.5 for him, which puts his score at 1.0 on the grid.
Ben takes the die and he too rolls a six. More cheers. He passes all six matches to Chuck. I record the same score for Ben as for Andy.
But Chuck rolls a three. So after he passes three matches to Dave, he still has three left in his bowl. And I note a loss of −0.5 on the chart.
Now Dave rolls the die; it comes up as a six. But he only has four matches to pass—the three that Chuck just passed to him and one from the last round. So he passes four to Evan. I write down a gain of +0.5 for him.
Evan gets a three on the die. So the lone match on the end of the table is joined by three more. Evan still has one left in his bowl. And I record a loss of −0.5 for Evan.
At the end of two rounds, this is what the chart looks like.