The Indian Clerk (5 page)
Authors: David Leavitt
The problem was what Hardy called the error term. The theorem inevitably overestimated the number of primes up to
n.
And though Riemann and others had come up with formulae to lessen the error term, no one had been able to get rid of it altogether.
This was where the zeta function came in. Hardy wrote it out on a blackboard:
The function, when fed with an ordinary integer, was fairly straightforward. But what if you fed it with an imaginary number?
And what was an imaginary number? He had to backtrack. "We all know that 1 × 1 = 1," he said. "And what does — 1 × — 1 equal?"
"Also 1," Strachey said.
"Correct. So by definition, the square root of — 1 doesn't exist. Yet it's a very useful number."
He wrote it in on the blackboard: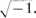
. "We call this number
i
."
He knew where this was going to lead: a long argument about the phenomenal and the real. If outside this room, Strachey said,
outside this Saturday evening,
i
was imaginary, then in this room, on this Saturday evening,
i
must be real. And why? Because in the world that was not this room, this Saturday evening, the opposite was true. For the
brethren, only the life of the meetings was real. Everything else was "phenomenal." Thus the Apostles embraced
i
without having the faintest idea what it meant.
After the talk was over, O. B. patted him on the back. "God willing, you'll be the man to prove it," he said, which was deliberate
provocation: O. B. knew as well as any of them that Hardy had long since renounced God, going so far as to ask the dean of
Trinity for permission not to attend chapel, and then, at the dean's insistence, writing to inform his parents that he was
no longer a believer. Gertrude pretended to weep, Mrs. Hardy wept, Isaac Hardy refused to speak to his son. A few months later,
his father contracted pneumonia, and Hardy's mother begged him to reconsider his choice. To placate her, he agreed to meet
with the vicar—the same, thin-fingered vicar by whom, years before, he'd been taken on a walk in the fog to discuss the kite.
While they talked, the vicar ate chocolates from a tray. At a certain point Hardy noticed that the vicar was glancing, not
very subtly, at his trousers.
Well, well,
he thought.
His father died the next evening. From that day on, Hardy never again set foot inside a Cambridge chapel. Even when some formal
protocol required him to go into a chapel, he refused. Eventually Trinity had to issue a special dispensation on his behalf.
By then, though, the college was more pliable. After all, Hardy was a don. And Oxford had sent out lures.
Occasionally, when he was working on the hypothesis, he'd remember his walk with the vicar. Looking for a proof, he'd think—
that's
like groping in a fog, feeling for a tug on the string. Somewhere high above you truth hovered—absolute, indisputable. When
you felt the tug, it meant that you'd found the proof.
God had nothing to do with it. Proof was what connected you to the truth.
And what of the tripos?
Halfway through his first year Hardy went to Butler, the master of Trinity, and announced that he was giving up mathematics.
He would rather change over to history, he said, return to Harold and the Battle of Hastings, than waste another minute in
the gloom of Webb's ugly house.
Butler had a gift for quick thinking. He rotated his wedding ring a quarter turn (this was his habit) and sent Hardy off to
talk to Love. Love, though an applied mathematician himself, recognized the source of Hardy's passion, and gave him a copy
of Camille Jordan's three-volume
Cours d'analyse de I'Ecole Poly technique.
This was the book, he later said, that changed his life, that taught him what it really meant to be a mathematician. Love
also persuaded Hardy that if he quit mathematics just to avoid the tripos, he would be submitting to its tyranny far more
completely than if he simply buckled down and took the thing.
The
Cours d'analyse,
Hardy told Littlewood, made the difference. The mere fact of knowing it awaited him on his shelf made it possible for him
to endure Webb's coaching. So he resumed the protocol of memorization, practice, memorization, and when June came, he went
to take the tripos with the first volume of the
Cours d'analyse
secreted in his coat pocket, as a talisman, and came out fourth wrangler.
For years afterward, naysayers grumbled that Hardy's subsequent determination to destroy the tripos was sour grapes, that
it owed entirely to his not being named senior wrangler. This he denied vociferously. Nor, he insisted, did his not being
named senior wrangler have anything to do with his decision, a month or so later, to leave Cambridge for Oxford. Had he been
named senior wrangler, or twenty-seventh wrangler, or wooden spoon, he would have done the same. For the grudge he bore was
not against the men who had scored higher than he had: it was against the tripos itself, and more generally, Cambridge, the
insularity of which the tripos embodied, and more generally still, England, its rigidity and smug, unquestioning belief in
its own superiority. In the end it took Moore to persuade him to stay. England, Moore told him, he could not remake. But perhaps
he could remake the tripos.
From then on, tripos reform became his crusade. He waged a campaign that was passionate, intelligent, and unrelenting, and
eventually, in 1910, he won: not only was the tripos modernized, the reading of the honors list was terminated. No longer
would wranglers and optimes stroll the avenues of Cambridge in June. No longer would wooden spoons be handed down from the
Senate House roof. Instead the tripos would be just another exam. None of which, he maintained, with just a hint of vexation
in his voice, had anything to do with his having been named fourth wrangler. After all, Bertrand Russell had been seventh
wrangler, and he was—well, Bertrand Russell. Had Hardy been senior wrangler, he would have felt the same way. Done the same
thing. It was important to him that strangers understood and believed this.
F
OR A WEEK, Hardy and Littlewood study the math. They sit together, either in Hardy's rooms or Littlewood's, with the pages
of the Indian's letter spread out before them, copying out the figures on a blackboard or on sheets of the expensive, creamy,
eighty-pound paper that Hardy uses exclusively for what he calls "scribbling." As they work, they drink tea or whiskey—all
this a deviation from their usual routine of postcards and letters, but one that the situation seems to demand.
There are clashes, and when they occur, it seems to Hardy that they are the clashes of spouses, not collaborators. "You always
have to finish the night so damn cheerful," Littlewood says one night as he's putting on his coat.
"What's wrong with that?"
"It's unrealistic, that's what. We work and work, we have to stop sometime, and you always make sure we stop when we think
we've untangled something."
"So? I like to go to bed feeling I've got something to look forward to in the morning."
"But what if in the morning we find out we've made a blunder? That we're wrong? Half the time we are."
"Then we'll work it out in the morning."
"I'd rather go to bed knowing the worst."
"Right, then. We'll stop when we're stuck. That way you can leave unhappy. Despairing. Gloomy. Is that what you'd prefer?"
"I do. Hope for the best, expect the worst, that's my philosophy."
Most nights they're up past one. They pick over Ramanujan's results, make sense of some, fail to make sense of others, and,
in the end, divide them into three rough categories: those that are either already known or easily deducible from known theorems;
those that are new, but interesting only because they are curious or difficult; and those that are new, interesting, and important.
All of it adds to their conviction that they are dealing with genius on a scale neither has ever imagined, much less encountered.
What Ramanujan has not been taught he has, using his own peculiar language, reinvented. Better yet, building on this foundation,
he has constructed an edifice of astonishing complexity, originality, and strangeness. Little of which Hardy indicates in
his reply, which he tries to keep as understated as he can manage. So far as the first group of results goes, he foregoes
confessing his amazement and offers only consolation, telling Ramanujan: "I need not say that if what you say about your lack
of training is to be taken literally, the fact that you should have rediscovered such interesting results is all to your credit.
But you should be prepared for a certain amount of disappointment of this kind." To the second and third groups, he devotes
more attention. "It is of course possible that some of the results I have classed under (2) are really important, as examples
of general methods. You always state your results in such particular forms that it is difficult to be sure about this."
They worked hard, he and Littlewood, on that last sentence. First Hardy wrote "peculiar" before "forms," but worried that
the word might put Ramanujan off. Then he crossed out "peculiar" and wrote "odd," which was worse. It was Littlewood who came
up with "particular," the slightly arch connotation of which (Hardy imagined Lytton Strachey saying it) he doubted that Ramanujan
would pick up on.
"It is essential that I should see proofs of some of your assertions," he writes next.
"Everything
depends on rigorous exactitude of proof."
His conclusion mixes encouragement with caution. "It seems to me quite likely that you have done a good deal of work worth
publication; and, if you can produce satisfactory demonstrations, I should be very glad to do what I can to secure it." Then
he signs his name, puts the letter in an envelope, addresses it, has it stamped, and on the morning of February 9th—the day
after his thirty-sixth birthday—slips it into the mouth of the postbox outside the Trinity College gates. For a time in his
childhood he believed that all the postboxes in the world were connected by a system of underground tubes; that when you mailed
a letter, it actually sprouted legs and ran to its destination. Now he imagines his letter to Ramanujan scuttling along the
passageways underlying England, crossing the Mediterranean and the Suez Canal, tirelessly trudging forward until it reaches
an address he can hardly visualize: Accounts Department, Port Trust, Madras, India.
And now he only has to wait.
New Lecture Hall, Harvard University
O
N THE LAST DAY of August, 1936, Hardy wrote on the blackboard behind him:
"I am sure that Ramanujan was no mystic," he said as he wrote, "and that religion, except in a strictly material sense, played
no important part in his life. He was an orthodox high-caste Hindu, and always adhered (indeed with a severity most unusual
in Indian residents of England) to all the observances of his caste."
Even as he spoke, though, he was doubting himself. He was giving, he knew, the script: the authorized version of his own opinion,
already at odds with other versions of Ramanujan's story, in particular those circulating in India, where the youth's piety
and devotion to the goddess Namagiri were situated at the dramatic heart of his mathematical discoveries.
Hardy did not—could not—believe this. His atheism was not merely part of his official identity; it was part of his being,
and had been since his childhood. Still, even as he uttered them, he had to admit that his words simplified considerably not
just the real situation but his own feelings about it.
He would have liked to put down his chalk at that moment, turn to his audience, and say something else. Something along the
lines of:
I don't know. I used to think I did. But as I get older it seems that I know less and less rather than more and more.
I used to believe that I could explain anything. Once, at Gertrude's request, I attempted to explain the Riemann hypothesis
to some girls at St. Catherine's School. This was during the early spring of 1913, when we were still awaiting Ramanujan's
reply to the first letter. I really thought that leading these girls through the steps of the Riemann hypothesis would be
easy, that I would awaken in them a fascination that would last them the rest of their lives. And so, while Gertrude stood
attendance with Miss Trotter, the maths mistress, a pale-faced young woman whose hair, though she could not have been more
than thirty, was already white, I lectured those girls in their starched pinafores. They gazed up at me with eyes that were
either love-struck or vacant or contemptuous. One chewed her hair. The Riemann hypothesis might be the most important unsolved
problem in mathematics, but that did not make it a subject of interest to twelve-year-old girls.
"Imagine," I said, "a graph, like any ordinary graph, with an
x
axis and a
y
axis. Let us say that the
x
axis is the ordinary number line, with all the ordinary numbers lined up in succession, and that the
y
axis is the
imaginary
number line, with all the multiples of / lined up in succession: 2/, 3.47/, 4,678,939/, and so on. On such a graph, as on
any graph, you can draw a point, and then connect the point, with lines, to points on the two axes. In this case, the numbers
that correspond to these points on the plane are called
complex numbers
because each one has a real part and an imaginary part. You write them like this: 2
i
+1. Or 4.6
i
+ 1736.34289 or 3
i
+ 0. The part with the / is the imaginary part, and corresponds to a point on the imaginary axis, while the other part is
the real part and corresponds to a point on the real axis.
"So this is the Riemann hypothesis: you take the zeta function and you feed it with complex numbers. And then you look at
your answers, and you see at which points the function takes the value of zero. According to the hypothesis, at every point
where the function takes the value of zero, the real part will have a value of
\
; or, to put it another way, all the points at which the function takes the value will line up along the line of
\
on the
x
axis, which is called the
critical line.
"To prove the hypothesis, you must prove that not a single zeta zero will ever be off the critical line. But if you can find
just one zeta zero off the line—just one zeta zero where the real part of the imaginary number
isn't 1/2
—then you'll have
disproved
the Riemann hypothesis. So half the job is looking for a proof—something airtight, theoretical—but half the job is hunting
for zeros. Counting zeros. Seeing if there are any that are off the critical line. And counting zeros involves some pretty
knotty math.
"And what will you have done, if you find the proof? You'll have eliminated the error term in Gauss's formula. You'll have
revealed the secret order of the primes."
That was it, more or less. Of course there was a lot that I left out: the so-called trivial zeros of the zeta function; and
the need, when exploring the zeta function landscape, to think in terms of four dimensions; and most crucially, the complex
series of steps that leads from the zeta function to the primes and their calculation. Here, if I had tried to explain, I
would have foundered. For there is a language that mathematicians can speak only among themselves.
After the lecture, the students applauded politely. Not for very long, but politely. I inspected their faces. They wore expressions
of boredom and relief. Already, it was obvious, they were thinking ahead: to hockey practice, or Gertrude's art class, or
a secret rendezvous with a boy. "Are there any questions?" Miss Trotter asked, her voice as colorless and icy as her hair,
and when no girl spoke, she filled in the void with her own words. "Do you believe, Mr. Hardy, in your heart of hearts, that
the Riemann hypothesis is true?"
I thought about it. Then I said, "Sometimes I do, sometimes I don't. There are days when I wake convinced that it's just a
question of counting zeros. Somewhere there must be a zero off the line. Then there are days when a stab of insight slices
right through me and I think I've made a step toward a proof."
"Could you give us an example?"
"Well, a few weeks ago, when
I was taking my morning walk—I take a walk every morning—it suddenly occurred to me how I might prove that there is an infinite
number of zeros along the critical line. I hurried straight home and wrote down my ideas, and now I'm very close to completing
the proof."
"But that means you've proven the Riemann hypothesis," Miss Trotter said.
"Far from it," I said. "All I'll have proven is that there is an infinite number of zeros along the critical line. But that
does not mean that there is not an infinite number of zeros not along the critical line." I watched her as she tried to untangle
the triple negative. Then I looked at Gertrude. It was clear that she had got the point before I'd even made it.
Afterward, when we were walking home together, I said to my sister, "This is why the Indian's letter interests me so much.
If, as he claims, he's significantly reduced the error term, then he may be on to Riemann."
"Yes," Gertrude said. "He may even be the man to prove Riemann. How would you feel if he did?"
"I'd be delighted," I said. She smirked. Of course she doubted—and was right to—my pose of selflessness. We stepped into the
house, where what seemed an infinity of maids was in the throes of an orgy of cleaning, Mother supervising their activities.
One swabbed the floor, another scrubbed the windows, a third was beating pillows. Suddenly I saw the maids as zeros of the
zeta function. I imagined them lining up, drawn as if by magnets along the critical line. There is a secret history through
which a monstrous housekeeper strides, destroying all she touches. According to O. B., a famous musician went deaf after taking
his housekeeper's advice that he treat an earache by stuffing cotton dipped in ether in his ears. And of course there was
Riemann's legendary housekeeper, who, upon learning of his death (if the story is to be believed), threw all of his papers—including
a reputed proof of the hypothesis—into the fire. How clearly I can envision that scene! The summer of 1866, warm weather,
and this vigorous woman—in many ways the most important figure in the history of mathematics—methodically feeding the pages
into the stove's stinking maw. Feeding and feeding, scrawled sheet after scrawled sheet, until, as legend has it, Riemann's
Gottingen colleagues arrive in a mob. Cry out for her to stop. Patiently they sort through what they have salvaged, praying
that the proof will have survived her reign of terror, while in the background . . . what does she do? Does she weep? Probably
not. I see her as plump, methodical. Energy without imagination. No doubt she goes about her business. Scrubbing down floors.
Washing pots.
The irony, of course, is that Riemann wasn't even there. He didn't witness, even in death, the conflagration. He had gone
to Italy, hoping the balmier weather would improve his health. He was thirty-nine when he died. Consumption.
And do you think his housekeeper imagined that somehow the papers themselves might be tainted?
People understood so little about contagion in those days.
I can't stop thinking about this woman. What I find most monstrous about her is her efficiency. It has a bloodthirsty edge.
In my mind I try to place myself at the scene in Gottingen. I try to explain to her, after the fact, the importance of the
documents she has destroyed. In response she simply gazes at me, as if I'm a perfectly benign idiot. Her belief in her own
rectitude is impregnable. This is the side of the German character that I preferred, before the war, not to contemplate, because
I could not reconcile it with my dream image of the German university town down the cobbled streets of which Gauss and Hilbert
strolled arm-in-arm, in defiance of fact, in defiance even of time. Ideas and ideals have a homey smell, rather like coffee.
And yet in the background there always lurks this housekeeper with her ammonia and her matches.