The Information (34 page)

Turing’s mother often asked him what use his mathematics had, and he told her as early as 1936 that he had discovered a possible application: “a lot of particular and interesting codes.” He added, “I expect I could sell them to H. M. Government for quite a substantial sum, but am rather doubtful about the morality of such things.”
♦
Indeed, a Turing machine could
make
ciphers. But His Majesty’s Government turned out to have a different problem. As war loomed, the task of reading messages intercepted from German cable and wireless traffic fell to the Government Code and Cypher School, originally part of the Admiralty, with a staff at first composed of linguists, clerks, and typists, but no mathematicians. Turing was recruited in the summer of 1938. When the Code and Cypher School evacuated from London to Bletchley Park, a country mansion in Buckinghamshire, he went along with a team that also included some champions at chess and crossword-puzzle solving. It was clear now that classical language scholarship had little to contribute to cryptanalysis.
The German system, named Enigma, employed a polyalphabetic cipher implemented by a rotor machine the size of a suitcase, with a typewriter keyboard and signal lamps. The cipher had evolved from a famous ancestor, the Vigenère cipher, thought to be unbreakable until Charles Babbage cracked it in 1854, and Babbage’s mathematical insight gave Bletchley early help, as did work by Polish cryptographers who had
the first hard years of experience with the Wehrmacht’s signal traffic. Working from a warren known as Hut 8, Turing took the theoretical lead and solved the problem, not just mathematically but physically.
This meant building a machine to invert the enciphering of any number of Enigmas. Where his first machine was a phantasm of hypothetical tape, this one, dubbed the Bombe, filled ninety cubic feet with a ton of wire and metal leaking oil and effectively mapping the rotors of the German device onto electric circuitry. The scientific triumph at Bletchley—secret for the duration of the war and for thirty years after—had a greater effect on the outcome than even the Manhattan Project, the real bomb. By the war’s end, the Turing Bombes were deciphering thousands of military intercepts every day: processing information, that is, on a scale never before seen.
Although nothing of this passed between Turing and Shannon when they met for meals at Bell Labs, they did talk indirectly about a notion of Turing’s about how to measure all this
stuff
. He had watched analysts weigh the messages passing through Bletchley, some uncertain and some contradictory, as they tried to assess the probability of some fact—a particular Enigma code setting, for example, or the location of a submarine.
He felt that something here needed measuring, mathematically. It was not the probability, which would traditionally be expressed as an odds ratio (such as three to two) or a number from zero to one (such as 0.6, or 60 percent). Rather, Turing cared about the data that
changed
the probability: a probability factor, something like the weight of evidence. He invented a unit he named a “ban.” He found it convenient to use a logarithmic scale, so that bans would be added rather than multiplied. With a base of ten, a ban was the weight of evidence needed to make a fact ten times as likely. For more fine-grained measurement there were “decibans” and “centibans.”
Shannon had a notion along similar lines.
Working in the old West Village headquarters, he developed theoretical ideas about cryptography that helped him focus the dream he had intimated to Vannevar Bush: his “analysis of some of the fundamental properties of general systems for the transmission of intelligence.” He followed parallel tracks all during the war, showing his supervisors the cryptography work and concealing the rest. Concealment was the order of the day. In the realm of pure mathematics, Shannon treated some of the same ciphering systems that Turing was attacking with real intercepts and brute hardware—for example, the specific question of the safety of Vigenère cryptograms when “the enemy knows the system being used.”
♦
(The Germans were using just such cryptograms, and the British were the enemy who knew the system.) Shannon was looking at the most general cases, all involving, as he put it, “discrete information.” That meant sequences of symbols, chosen from a finite set, mainly letters of the alphabet but also words of a language and even “quantized speech,” voice signals broken into packets with different amplitude levels. To conceal these meant substituting wrong symbols for the right ones, according to some systematic procedure in which a
key
is known to the receiver of the message, who can use it to reverse the substitutions. A secure system works even when the enemy knows the procedure, as long as the key remains secret.
The code breakers see a stream of data that looks like junk. They want to find the real signal. “From the point of view of the cryptanalyst,” Shannon noted, “a secrecy system is almost identical with a noisy communication system.”
♦
(He completed his report, “A Mathematical Theory of Cryptography,” in 1945; it was immediately classified.) The data stream is meant to look stochastic, or random, but of course it is not: if it were truly random the signal would be lost. The cipher must transform a patterned thing, ordinary language, into something apparently without pattern. But pattern is surprisingly persistent. To analyze and categorize the transformations of ciphering, Shannon had to understand the patterns of language in a way that scholars—linguists, for example—had never done before. Linguists had, however, begun to focus their discipline on structure in language—system to be found amid the vague billowing shapes and sounds. The linguist Edward Sapir wrote of “symbolic atoms” formed by a language’s underlying phonetic patterns. “The mere sounds of speech,” he wrote in 1921, “are not the essential fact of language, which lies rather in the classification, in the formal patterning.… Language, as a structure, is on its inner face the mold of thought.”
♦
Mold of thought
was exquisite. Shannon, however, needed to view language in terms more tangible and countable.
Pattern, as he saw it, equals redundancy. In ordinary language, redundancy serves as an aid to understanding. In cryptanalysis, that same redundancy is the Achilles’ heel. Where is this redundancy? As a simple example in English, wherever the letter
q
appears, the
u
that follows is redundant. (Or almost—it would be entirely redundant were it not for rare borrowed items like
qin
and
Qatar
.) After
q
, a
u
is expected. There is no surprise. It contributes no information. After the letter
t
, an
h
has a certain amount of redundancy, because it is the likeliest letter to appear. Every language has a certain statistical structure, Shannon argued, and with it a certain redundancy. Let us call this (he suggested)
D
. “
D
measures, in a sense, how much a text in the language can be reduced in length without losing any information.”
♦
Shannon estimated that English has redundancy of about 50 percent.
♦
Without computers to process masses of text, he could not be sure, but his estimate proved correct. Typical passages can be shortened by half without loss of information. (
If u cn rd ths
…) With the simplest early substitution ciphers, this redundancy provided the point of first weakness. Edgar Allan Poe knew that when a cryptogram contained more
z
’s than any other letter, then
z
was probably the substitute for
e
, since
e
is the most frequent letter in English. As soon as
q
was solved, so was
u
. A code breaker looked for recurring patterns that might match common words or letter combinations:
the, and, -tion
. To perfect this kind of frequency analysis, code breakers needed better information about letter frequencies than Alfred Vail or Samuel Morse had been able to get by examining printers’ type trays, and anyway, more clever ciphers overcame this weakness, by constantly varying the substitution alphabet, so that every letter had many possible substitutes. The obvious, recognizable patterns vanished. But as long as a cryptogram retained any trace of patterning—any form or sequence or statistical regularity—a mathematician could, in theory, find a way in.
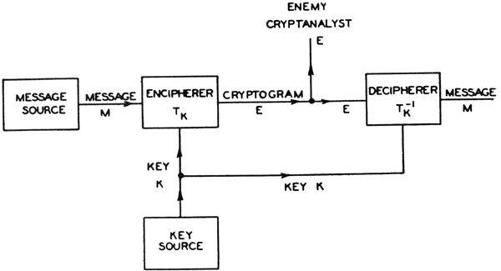
What all secrecy systems had in common was the use of a key: a code word, or phrase, or an entire book, or something even more complex, but in any case a source of characters known to both the sender and receiver—knowledge shared apart from the message itself. In the German Enigma system, the key was internalized in hardware and changed daily; Bletchley Park had to rediscover it anew each time, its experts sussing out the patterns of language freshly transformed. Shannon, meanwhile, removed himself to the most distant, most general, most theoretical vantage point. A secrecy system comprised a finite (though possibly very large) number of possible messages, a finite number of possible cryptograms, and in between, transforming one to the other, a finite number of keys, each with an associated probability. This was his schematic diagram:
The enemy and the recipient are trying to arrive at the same target: the message. By framing it this way, in terms of mathematics and probabilities, Shannon had utterly abstracted the idea of the message from its physical details. Sounds, waveforms, all the customary worries of a Bell Labs engineer—none of these mattered. The message was seen as a choice: one alternative selected from a set. At Old North Church the night of Paul Revere’s ride, the number of possible messages was two. Nowadays the numbers were almost uncountable—but still susceptible to statistical analysis.
Still in the dark about the very real and utterly relevant experience at Bletchley Park, Shannon built an edifice of algebraic methods, theorems, and proofs that gave cryptologists what they had never before possessed: a rigorous way of assessing the security of any secrecy system. He established the scientific principles of cryptography. Among other things, he proved that perfect ciphers were possible—“perfect” meaning that even an infinitely long captured message would not help a code breaker (“the enemy is no better off after intercepting any amount of material than before”
♦
). But as he gave, so he took away, because he also proved that the requirements were so severe as to make them practically useless. In a perfect cipher, all keys must be equally likely, in effect, a random stream of characters; each key can be used only once; and, worst of all, each key must be as long as the entire message.
Also in this secret paper, almost in passing, Shannon used a phrase he had never used before: “information theory.”
First Shannon had to eradicate “meaning.” The germicidal quotation marks were his. “The ‘meaning’ of a message is generally irrelevant,” he proposed cheerfully.
♦
He offered this provocation in order to make his purpose utterly clear. Shannon needed, if he were to create a theory, to hijack the word
information
. “ ‘Information’ here,” he wrote, “although related to the everyday meaning of the word, should not be confused with it.” Like Nyquist and Hartley before him, he wished to leave aside “the psychological factors” and focus only on “the physical.” But if information was divorced from semantic content, what was left? A few things could be said, and at first blush they all sounded paradoxical. Information is uncertainty, surprise, difficulty, and entropy:
- “Information is closely associated with uncertainty.” Uncertainty, in turn, can be measured by counting the number of possible messages. If only one message is possible, there is no uncertainty and thus no information.
- Some messages may be likelier than others, and information implies surprise. Surprise is a way of talking about probabilities. If the letter following
t
(in English) is
h
, not so much information is conveyed, because the probability of
h
was relatively high. - “What is significant is the difficulty in transmitting the message from one point to another.” Perhaps this seemed backward, or tautological, like defining mass in terms of the force needed to move an object. But then, mass
can
be defined that way. - Information is entropy. This was the strangest and most powerful notion of all. Entropy—already a difficult and poorly understood concept—is a measure of disorder in thermodynamics, the science of heat and energy.