The King of Infinite Space (14 page)

And Euclid's parallel postulate is false.

W
ITH A FEW
simple straight lines, Nikolai Ivanovich Lobachevsky had placed the denial of Euclid's parallel postulate squarely on the flat Euclidean page. The theorems that he derived in his masterpiece he derived properly. They followed impeccably from the axioms of neutral geometry and the denial of Euclid's parallel postulate. The engine of inference purred without pause.

But if the denial of Euclid's parallel postulate is to be convincing, it requires more than a derivation. It demands a model and so a way of being true. Illustrations have done what illustrations can do. If no model is forthcoming, there is no reason to suppose that the denial of the parallel postulate and the axioms of neutral geometry are consistent, mutually life-enhancing. If they are not, we are returned to the logical point from which non-Euclidean geometry represented a flight. An inconsistency would indicate a contradiction between the denial of the parallel postulate and the axioms of neutral geometry.

And this is precisely what no mathematician had been able to discover.

P
ICTURES WHEN THEY
appeared were for this reason welcomed. They revealed a world that might satisfy the axioms of non-Euclidean geometry. They were a source of inspiration and so a source of comfort.

It could be done. That is what the models suggested.

The
Kazan Messenger
had come and gone, when in 1868, the Italian mathematician Eugenio Beltrami published his influential study, “Saggio di interpretazione della geometria non-euclidea” (A study of the interpretation of non-Euclidean geometry). With the study, a model: the Beltrami pseudosphere. The pseudosphere is odd enough to prompt the suspicion that on its surface,
anything
might be true.

Illustrations of the Beltrami pseudosphere are vivid and often lovely, but they are incomplete (
Figure IX.2
). For one thing, the middle of the pseudosphere is girdled by what is plainly a Euclidean annulus or ring. What is that doing there? And for another thing, the
embouchure
of the pseudosphere's horns, where a divine trumpeter might have placed his lips, recedes in real life into the infinite distance. This no illustration can show.

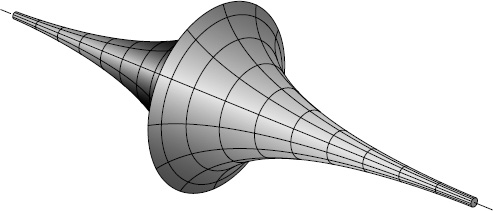
F
IGURE
IX.2.
Beltrami pseudosphere

If illustrations of the Beltrami pseudosphere are not complete, they are nevertheless exhilarating. They show a universe coming to quicken. Shapes hidden by Lobachevsky's proofs come to life in Beltrami's picture. The triangle is an example. The Euclidean triangle is a familiar shape of art and architecture, its sides soaring or squat. When inscribed on the Beltrami pseudosphere, Euclidean triangles sag inwardly, their sides concave, and their interior angles compromised from the first by the negative curvature of their surface (
Figure IX.3
). The interior angles of a triangle on a pseudosphere sum to
less
than two right angles. On a sufficiently curved surface, those interior angles are lucky to sum to anything at all.

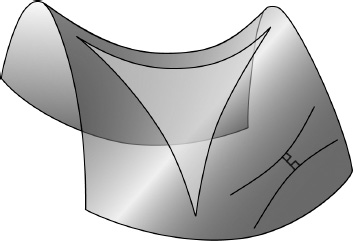
F
IGURE
IX.3.
Hyperbolic triangle

I
N
1880,
THE
superb French mathematician Henri Poincaré added another model to the growing gallery of non- Euclidean models, and in the Poincaré disk, another picture. The Beltrami pseudosphere invites the mathematician to seize it by its two horns and, perhaps, give it a toot. No one is about to seize the Poincaré disk. Among mathematicians who understood its nature, no one was tempted to go near it.

The Poincaré disk divides the Euclidean plane into three distinct regions of space. There are those points lying
beyond
the disk, those
on
its circumference, and those
in
its interior. From the outside, the disk is simply a little unit circle, as fixed and finite as a penny. From the inside, it encompasses the whole of the infinite hyperbolic plane. Outside the circle, everything is Euclidean, and inside, everything hyperbolic. Outside and inside are Euclidean from the outside, but hyperbolic from the inside. The inside is accessible from the outside—
step right in
—but not the outside from the inside—
no exit
.

There is no distinction between Euclidean and hyperbolic points. Points are points. Hyperbolic lines are otherwise. They are not like Euclidean lines at all and require careful definition. Those careful mathematical definitions express and make precise something like a dream sequence in which the Poincaré disk floats serenely in the Euclidean plane, a circle among other circles. Now and then, a drifting
circle penetrates the circumference of the Poincaré disk, depositing, before it drifts on, the trace of a circumferential arc on its interior, one meeting the circumference at right angles. These Euclidean arcs are the straight lines of the hyperbolic plane. They are lines because they are lines, and they are straight because, although curved on the outside, they are straight on the inside (
Figure IX.4
).

F
IGURE
IX.4.
Poincaré disk

I
N NON
-E
UCLIDEAN
geometry, ideas that in most circumstances would fly apart stick together. This is especially true of the Poincaré disk. The binding force required to make fly-apart ideas stick together is expressed by the definition of hyperbolic distance. In the Euclidean plane, the distance
d
(
x, y
) between two points
x
and
y
is the length of the straightest line joining them:
ds
²
=
dx
²
+
dy
²
. Square roots
are squared in this formula to preserve the positive character of distance itself. Distances cannot be negative. But Euclidean distances are unavailing inside the Poincaré disk. Their introduction there would do nothing more than ratify all the old Euclidean postulates and prejudices. There is, instead, hyperbolic distance, a measure that justifies, if anything does, the designation of the disk as deviant.

To define the hyperbolic distance between any two points in the Poincaré disk requires, as one might expect, a number of unfamiliar ideas. But some sense of deviant distance is accessible by means of a formula that traces only the distance from the center of the Poincaré disk to its circumference. Once given, the full definition of distance follows. The formula is
ds
= 2
dr
/1 −
r
²
. The symbol
ds
designates the hyperbolic distance of a radial line originating in the center of the disk and proceeding sedately to its circumference. The symbol
dr
measures its
Euclidean
distance. Two different measures of distance have been assigned to one and the same line, but they are codependent. Hyperbolic distance has been defined in terms of Euclidean distance. The question of the distance from the center of the disk to its circumference thus receives two quite distinct answers. Standing beyond the boundary of the Poincaré disk, the Euclidean geometer sees that the circumference of the disk is along its radius one unit away from its center.
How far? Not far
. But as
r
approaches 1,
ds
approaches infinity. Standing at the center of the disk and then trudging in any direction, the hyperbolic geometer sees the circumference eternally receding.
How far? Very far
.

Differences in distances ramify throughout the hyperbolic plane. The Euclidean geometer will observe from well beyond the disk that within the disk, distances contract as his hyperbolic colleague advances on a line toward the boundary. That poor fat fool is shrinking before his eyes. This the hyperbolic geometer does not see at all. He is in his advance toward the boundary precisely as he was reposing at its center. Everything is as it was.

T
HE DEFINITION OF
distance by which the hyperbolic world is ruled brings about the failure of Playfair's axiom. The curved lines throughout the disk are straight because they are geodesics, and they are geodesics because they represent the shortest distance between two points. The Euclidean geometer can cast a cold eye into the Poincaré disk and see why Euclid's parallel postulate fails.

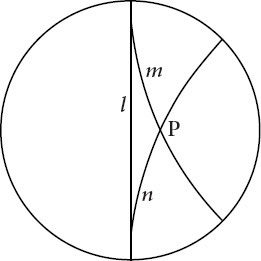
T
HE POINT
P
lies somewhere on the disk, and two lines
m
and
n
pass through
P
, both of them approaching the circumference at two different points
A
and
B
, the place—the very place—at which AB itself passes through the circumference on its way toward strictly Euclidean glory.

The chord PA is parallel to
l
because PA and AB do not intersect
within
the Poincaré disk. How could they? In A, they have a common point of intersection at the boundary. Strictly Euclidean, that point of intersection is located beyond the interior of the disk. Considered as hyperbolic lines, both AB and PA are infinitely far from A.

Thus AB has in PA one parallel line meeting the conditions of Playfair's axiom.

But AB meets the circumference
twice
, once at A and again at B. Two lines pass through P, and
both
are parallel to AB.

P
OINCARÉ WAS A
powerful mathematician and a subtle philosopher. He had induced the pendulum to swing wide, but he knew all about pendulums, and knew perfectly well that having swung wide, they have a tendency to swing back.

“Let us consider a certain plane,” Poincaré wrote in a brilliant little book,
Science and Hypothesis
, “which I shall call the fundamental plane, and let us construct a kind of dictionary by making a double series of terms written in two columns, and corresponding each to each, just as in ordinary dictionaries the words in two languages which have the same signification correspond to one another.” The words contained in this dictionary are
space
,
plane
,
line
,
sphere
,
circle
,
angle
,
distance
, and the like:

With these remarks, Poincaré invited an affronted common sense to reacquire a say in the Euclidean Joint Stock Company. The theorems of hyperbolic geometry are theorems of Euclidean geometry; they are theorems of Euclidean geometry disguised by a new, radical definition of distance. On back translation, the disguise drops away. Familiar old faces appear again. Euclidean and hyperbolic geometry are
not
two entirely different theories. They coincide in their assessment of the truth. There is amity between them.