The King of Infinite Space (9 page)

Although Euclid begins his proof with proposition twenty-seven taken straight-up, his argument depends on its contrapositive: if AB is not parallel to CD, then AEF and EFD are not equal.

In order to demonstrate this proposition, Euclid undertakes a maneuver that is common throughout mathematics and therefore throughout geometry. By dividing his mind, he assigns to one half the position he wishes to rebut, and to the other half, the ensuing right of ridicule. The technique is known as
reductio ad absurdum
, or proof by contradiction. Euclid's strategy is to prove that a proposition is true by assuming that it is false, and then demonstrating what a mess that makes.

From the assumption that the contrapositive to his twenty-seventh proposition is false, Euclid will show that AEF and EFD are equal
and
that they are not.

This is the mess.

E
UCLID
'
S PROOF IS
not self-contained. If it were, there would be no reason to place twenty-six proofs before it. Proposition twenty-seven employs Euclid's sixteenth proposition
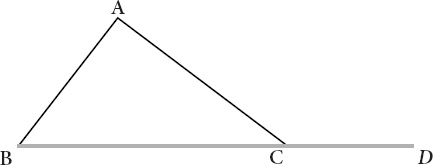
and his nineteenth and twenty-third definitions. The sixteenth proposition says that in any triangle, if one of the sides is extended, the exterior angles must be greater than either of the interior and opposite angles.
Figure VII.2
carries an enviable air of visual authority: angle ACD is greater than angles CBA or BAC. The twenty-third definition has something to say about parallel lines—among other things, if two lines are not parallel, then sooner or later they must meet at a point.
²
His nineteenth definition offers the obvious and expected account of just which figures are triangles.

F
IGURE
VII.2.
Proposition sixteen

Euclid is ready now to argue. His claim is that if AB is not parallel to CD, then the angles AEF and EFD shown in
Figure VII.1
are not equal. So begin with this. And suppose the proposition false. If false, its antecedent must be true: AB is not parallel to CD. And if false, its consequent must be false: AEF and EFD are equal.

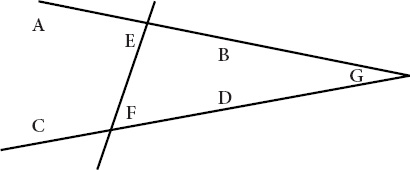
If AB is not parallel to CD, then these lines must meet at a point G. It is here, and only here, that Euclid's own diagram plays a role.
Figure VII.3
does one thing. It illustrates the supposition that AB is
not
parallel to CD, the antecedent—and
only
the antecedent—of the proposition Euclid means to reject. The figure is as spare and unforgiving as a sneer. It does not show lines AB and CD converging toward G. Were Euclid to have been interrogated on this point, he might have said with perfect aplomb, Why should I have bothered?

F
IGURE
VII.3.
Proposition sixteen, Euclid's diagram

Why
should
he have bothered?

Given that AB and CD meet at G, Euclid next constructs the triangle GEF. He requires his nineteenth definition and
his first axiom, the latter to connect the dots and the former to say what they mean. Euclid's sixteenth proposition affirms that if in any triangle one of the sides is extended, then the exterior angles must be greater than either of the interior and opposite angles. The denial of Euclid's twenty-seventh proposition has encountered Euclid's antecedent proof of proposition sixteen. The turning point of the proof has arrived.

And while Euclid provides no diagrams to illustrate this point, a diagram is easy to contrive (
Figure VII.4
). The balance of Euclid's proof is now a matter of stating the obvious. From his sixteenth proposition, Euclid has concluded that AEF and EFD
cannot
be equal. But from his assumption that his twenty-seventh proposition is false, Euclid has also concluded that AEF and EFD
must
be equal. The result is the foreseen shambles: AEF and EFD are both equal and unequal.

F
IGURE
VII.4.
Contrapositive to proposition twenty-seven

We may allow Euclid to dissolve the distinctions in his mind between back and forth. The denial of proposition twenty-seven had led to a contradiction. Therefore the proposition must be true. Euclid has persuaded himself of himself.

E
UCLID
'
S
ELEMENTS
REMAINS
locked in the world before our own, and it thus demands the kind of richly imagined embedding still demanded by Watteau. The painting or the Euclidean diagram is a slice of a temporal continuum, the mind placing in proper perspective the slices that have gone before and those that go afterward.

The purpose of a proof is to compel belief, and to compel his reader's belief, Euclid has invested his twenty-seventh proposition with pictorial life. His diagram and the logical structure of the theorem it expresses undergo fusion. Far more than the axiomatic method alone, it is this fusion that is at the heart of Euclid's method.

In
Figure VII.1
, lines drawn parallel strike off for the infinite, always together, and by the same distance, too, but always apart, doomed thus to travel in companionable isolation throughout the whole of space.
Figure VII.3
, by contrast, expresses the contrapositive kernel of Euclid's argument. It offers a lucid and balanced view into the future, but a view narrowed to a single pictorial and geometrical point. The lines are not parallel; therefore, they meet at a point.

Euclid's single diagram leads backward and forward by means of a sequence that Euclid expects the reader to create and then complete, a night series of shapes, fluid and fantastic, the day's unrelenting logic dissolved. Parallel lines bend toward one another, drooping in defiance of the facts, and deflected from parallel position, they converge toward some point G, and converging toward some point G, they register an effect at a distance, and an effect registered, angles change, and the angles changing, “Well, you know or don't you kennet or haven't I told you every telling has a taling and that's the he and the she of it, Look, the dusk is growing. My branches are taking root.”
¹

Figures VII.1
and
VII.3
depict worlds in counterfactual collision. Lines that are parallel in
Figure VII.1
are
not
parallel in
Figure VII.3
. But worlds in collision on the level of the image represent worlds in collusion on the level of the theorem. Having grasped his proof, you will, Euclid is persuaded, understand its illustration, for with his exquisite power to unify the logical structure of his proof and the diagrams by which the proof is conveyed, he has illustrated a temporal flow.

As far as Euclid the Magician is concerned, nothing more need be done. He has gotten you to do something rapid, unconscious, and not entirely certain.

As far as Euclid the Logician is concerned, nothing more need be added. He has gotten you to see a sequence of propositions hurtling toward a contradiction.

As far as Euclid the Geometer is concerned, nothing more need be done or added.

T
HE PROPOSITIONS THAT
Euclid demonstrated in the
Elements
ascend by number, and the numbers are a reasonable guide to their difficulty. Euclid's twenty-seventh proposition retains something of the obvious. It encourages the student (or the reader) to a concurrent grunt of affirmation. The theorem is dramatic nevertheless in its reach and power. It draws a connection between a pair of equal angles on the one hand and a pair of parallel lines on the other.

A look is enough to gauge the character of an angle, but no look, however lingering, does much to determine the character of parallel lines. Straight lines are parallel if they never meet. Within the Euclidean plane,
never
goes on and on. How is the geometer to establish that lines that never met will never meet? Once they have passed the last point of public inspection, lines that seem parallel might willfully undertake an unexpected decision to draw close after all.

But equal angles are equal locally, visible in the here and now. By checking the angles made by certain straight lines, the geometer may determine their parallel character once and for all. There is no need to track them to the back of beyond.

This theorem is interesting without in any way being extraordinary. What is extraordinary is what is so often hidden in the
Elements
: the rich ensemble of instruments that Euclid has employed to serve his ends. The proof of proposition twenty-seven is entirely a matter of the scant few lines needed to move with logical assurance from Euclid's premises to his conclusions. But like an army, every one of Euclid's theorems carries a long logistical tail: its apparatus of propositions, axioms, definitions, common notions, and rules of inference. And its illustrations, those diagrams that provide an intuition that is “rapid, unconscious, and not entirely certain.”

No part of this immense logistical tail by itself compels belief or elicits assent. It was Euclid's genius to grasp the whole and to trust in the reader to follow what he had grasped.

 

1
.
Euclid's twenty-seventh proposition may suggest Euclid's original parallel postulate. This is incorrect. Euclid's twenty-seventh proposition is inverse to Euclid's parallel postulate and so logically equivalent to its
converse.

2
.
Euclid's twenty-seventh proposition is logically equivalent to Euclid's sixteenth proposition, something that the logician August De Morgan observed in the nineteenth century. Euclid might well have begun with his sixteenth proposition and after demonstrating it, arrived at his twenty-seventh proposition by contraposition. The resulting proof would have been impeccable, but it would not have directly mentioned those parallel lines bound for far places that figure in his twenty-seventh proposition. To get them to come forward, he would have had to reverse logical steps and restore the original proposition.

1
.
James Joyce,
Finnegan's Wake
, Library of the University of Adelaide, South Australia, 2005, p. 213.

I
F THERE ARE
numbers
and
there are shapes in nature, which comes first?

Common sense: neither.

First in
what
?

Although Euclid's
Elements
is a treatise about geometry, some idea of the natural numbers 1, 2, 3, . . . is present as background. It could not be otherwise. Euclid talks of triangles, after all, meaning more than
one
, and there is
one
and only
one
line parallel to a given line specified by Playfair's axiom. The natural numbers are among the common notions “on which all men base their proofs.” The reverse is
true as well. No mathematician could study arithmetic if the numerals did not have stable geometrical properties. Imagine trying to prove that 2 plus 2 is 4 and seeing the numeral “2” undertake a sinuous deformation on the blackboard, or in the mathematician's mind, vanishing, perhaps, at the very moment of intellectual triumph.