The King of Infinite Space (6 page)

How might this have worked? Ancient geometers were divided. A right angle?

Before right angles are declared equal it would be immensely helpful to know what an angle is in the first place. In this respect, Euclid's axiom is rather like the declaration that all close siblings are competitive. What is a sibling? But then again, what is an angle?

Euclid does say in his eighth definition that “a plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.” In his very next definition, Euclid seems to suggest that an angle is what, by his previous definition, an angle
contains
. It is better not to go there. Revising Euclidean geometry early in
the twentieth century, David Hilbert considered Euclid's eighth definition and thought that with a bit of polish, it would do nicely, the brass showing through the smudge (see
Chapter VIII
for Hilbert's system). “Let α be any arbitrary plane,” Hilbert writes, “and
h
,
k
any two distinct half-rays lying in α and emanating from the point O so as to form a part of two different straight lines. We call the system formed by these two half-rays
h
,
k
an angle.” An angle is thus a matter of two straight lines suavely exiting a common point.

But Hilbert's definition invites the question when these systems are the same, and when they are different.

Euclid and Hilbert both required some general principle under which angles of any size are judged equal or unequal. A principle is easy enough to contrive. Consider two angles separated widely in space. Two angles and so two systems. Two systems and so four straight lines. Four straight lines and so two points. Two such systems, and so two such angles, are equal if they coincide.

Euclid and Hilbert appear well satisfied.

But to determine whether two angles separated in space coincide, both Euclid and Hilbert must suppose that one of them is moved so that it is imposed on the other. But if moved, then moved in such a way that its
own
angle remains unchanged. This requires a commitment to the homogeneity of space, the idea that as they are moved in space, Euclidean figures do not change in shape. How might
this be established without an antecedent account of the identity of their angles?

It is not so much that Euclid's definition is smudged. There seems to be no brass underneath the definition, no matter how much polish is applied to its surface.

T
HE FIFTH AND
final axiom of Euclid's system is more famous than the other four. It is said to have troubled Euclid, who squirmed and turned, wheezed and whistled, before accepting it:

5.
If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on the side on which are the angles less than two right angles.

The axiom is troubling because it seems to assess the property of parallelism by an appeal to what it is not. The theorem's two straight lines converge at a point; they are not parallel. The subject of Euclid's fifth axiom happens to be lines that
are
parallel. What about them?

An eighteenth-century form of the axiom credited to the Scottish mathematician Francis Playfair is far more intuitive than Euclid's own, and as mathematicians almost at once realized, both versions are logically equivalent:

5a.
One and only one straight line may be drawn through any point P in the plane parallel to a given straight line AB.

The phrase “may be drawn” is permissive when permission is not needed. The axiom affirms that in addition to being unique—“one and only one”—a line parallel to AB and passing through P
exists
.

Point taken, motion adopted. Playfair's axiom says that through a point outside a given line, there exists one and only one line parallel to the given line.

Playfair's axiom completes the axiomatic structure of Euclidean geometry.

It is the last.

E
UCLID WAS SAID
to be troubled by this axiom because it seemed more complicated than the others. On other accounts, it seemed to him less evident. And still other accounts ascribe to Euclid the contrary conviction that the parallel postulate is simple enough to be a theorem. Those doubts of his are today taken as evidence of Euclid's superb logical intuition. He knew something was wrong, or if not wrong, then not right.

It would be fine to have a Euclidean double willing to join the discussion and enter into the record a few doubts about these doubts. What might he say—this Euclid scrabbling
along the path the real Euclid never chose? For one thing, he would, I hope, reject the idea that the fifth axiom is more complicated than the other axioms. Complexity requires a measure or metric, and neither is in the case of these axioms forthcoming. I am sure that a geometer might be found championing the first of Euclid's axioms as more complicated than all the others, just for the heck of it. The fact that Playfair's axiom is simpler than the axiom Euclid introduced is evidence that one and the same axiom may have both a simple and a complicated formulation.

An imaginary Euclid might be equally inclined to disabuse the real Euclid of his
petit soucis
that his fifth axiom might not be evident.
Mais non
! If an axiom is not self-evident, then somehow it must encourage the suspicion, however long deferred, that it might be false. For this reason, no one supposes that the statement that snow is white is self-evident. True, yes; evident on inspection, that, too; self-evident, no. The denial of self-evidence requires some imaginative contingency of the snow is white but it might have been black variety.

But Euclid's parallel postulate is true under the circumstances that Euclid sketched on a brimming dust board, and there is no obvious way in which it might be false. The parallel axiom is obviously not provable; an axiom is an assumption. But neither is the axiom obviously deniable. If it were obviously deniable, it would be possible obviously to deny it.

How would that proceed, that imaginative exercise?

Still, modern mathematicians have seen better and seen further than either of our Euclids. The parallel postulate is anomalous. It is not necessary. It can lapse.

But in every single world in which the parallel postulate fails, it fails either because the underlying space has changed, or because certain common geometrical terms such as distance have been given a new meaning. In the contrived universe that Euclid limned, it does not fail at all.

E
UCLID
'
S
ELEMENTS
BELONGS
to a curious tradition, one that it created and now incarnates—the mountain- climbing pastoral. Mathematicians regard themselves as men of ascent. “Mathematical study and research are very suggestive of mountaineering,” the English mathematician Louis Joel Mordell remarked, recalling with satisfaction that when Edward Whymper made the first ascent of the Matterhorn, four of his colleagues perished on the climb. The genre is pastoral because the
Elements
expresses Euclid's intense demand for an idealized world, one in which things are free of friction and inferences smooth as ice. In his influential study,
Some Versions of Pastoral
, William Empson identified the pastoral with the imperative to “put the
complex into the simple.” What could be more Euclidean? Euclid's
Elements
is that rare thing: its own best example.

If the theorems of Euclid's
Elements
are its peaks, the proofs are a record of his climbs. In some, Euclid gets to the top quickly; in others, he is obliged to grunt and slog, and in these he is like some grizzled old climber recalling how once he was threatened by congelation of the anus. No matter the proofs that he offers, Euclid expects the reader to grasp the drama that they encompass. The proofs communicate tension, release, triumph. They allow the reader to experience the author's discomfort at a distance.

But why do what Euclid has done already?
The base angles of an isosceles triangle are equal
. This is Euclid's fifth proposition. What is the point in proving it all over again? If the question is surprisingly common, the Euclidean answer is uncommonly stern. Euclid regarded demonstrative ascent as its own reward. “There is no royal road to geometry,” he contemptuously remarked when some ignominious Ptolemy (Ptolemy Soter) complained that his proofs were too difficult.

No work, nothing gained; no work, nothing learned; no work, nothing.

This, too, is a part of the Euclidean tradition, its moral urgency.

G
EORGE
M
ALLORY ATTEMPTED
to reach the summit of Mount Everest in 1924, and died in the attempt. Under circumstances
less demanding than Everest, fellow climbers observed, Mallory would simply swarm up a mountain, like an energetic quadruped. This is not Euclid's way. His proofs are composed of small, mincing, but precise and delicate, logical steps. They must be undertaken one after the other. Not easy. And not easy because the method of proof is one thing; its subject, another. But Euclidean geometry involves the same bifurcation of attention that characterizes the physical sciences. To describe the arc of a cannonball in flight, the physicist, wishing more precision than might be afforded by
there she goes
, must use the analytic apparatus of the differential calculus. The calculus is new; the pattern, old. It is a pattern precisely as old as the
Elements
.

A Euclidean proof does not lend itself to light reading. Each step is easy enough because each step is small enough, but steps cannot be skipped, and retaining in mind all the steps involved in a proof—this is very difficult. A complicated differential diagnosis in medicine, or a brief in contract law, is not easy to read either, but a Euclidean proof, although stripped down because abbreviated by symbols, is difficult in a way in which documents in medicine or the law never are. Pencil and paper are helpful. Diagrams are fine. Euclid's
Elements
is illustrated. Patience is required, no doubt, and beyond that, a taste for alpine altitudes.

Do not take my word for it: consider the master.

“On a given finite straight line,” Euclid says, it is always possible “to construct an equilateral triangle.”

These are the first words of his first proof. In his nineteenth and twentieth definitions, Euclid defines rectilinear figures—figures contained by straight lines—and equilateral triangles: triangles with three equal sides. But neither his definitions, his common notions, nor his axioms say that any of them exist, and in nothing that has come before has Euclid given the slightest indication that it is within his power to make or create them.

In stating his first theorem, Euclid uses the infinitive
to construct
. I have used
to create
. In fact, nothing is either constructed or created. The equilateral triangles are there all along. Euclidean triangles are abstract: the
Elements
does not describe anything physical, and pure Platonic triangles do not come into and out of existence. Euclid's proof reveals them as shapes in the sense that his axioms establish them as objects. The Euclidean maneuver has something in common with revealed checkmates in chess, in which some irrelevant piece is shuffled to reveal the devastating and inexorable combination that it has disguised. And something in common with certain landscape experiences, the hillock having been ascended, the peak long hidden suddenly revealed.

“L
ET
AB
BE
a given finite straight line.”

Using A as a fixed point, Euclid at once deduces the existence of the circle BCD and appeals to his own third axiom to justify this step (
Figure VI.1
).

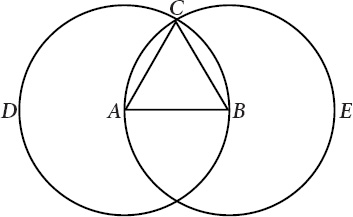
F
IGURE
VI.1.
Proposition one

One circle deserves another: this one, ACE, whose center is B. The third axiom—again.

These circles, Euclid now asserts, must meet at a point C. But by Euclid's first axiom, any two points determine a straight line. Thus the lines CA from C to A, and CB from C to B.

With these straight lines deductively established, the triangle ABC appears; its base is the straight line AB with which Euclid began his proof, and its sides are the straight lines CA and CB. (It hardly matters, I should say, whether the straight line CA is designated as CA or AC—although, I suppose, some logical maniac might ask why it does not matter.)