The King of Infinite Space (8 page)
Read The King of Infinite Space Online
Authors: David Berlinski

I
N ANY RIGHT
-
ANGLED
triangles, Euclid says, the square on the side subtending the right angle is equal to the squares on the sides containing the right angle. Two things are equal to one. Not numbers, but shapes. But if shapes, then
numbers, too. The area of a square expresses the squaring of a number.
Throughout Euclid's proof, the right triangle ABC exerts a dark magnetic force on his imagination (
Figure VI.3
). Its sides AB and AC are
the
sides of the Pythagorean theorem, and its hypotenuse BC,
the
hypotenuse. Everything else in the diagram is ancillary and will, when the proof is complete, be allowed to fall away, like the scaffold supporting an arch.
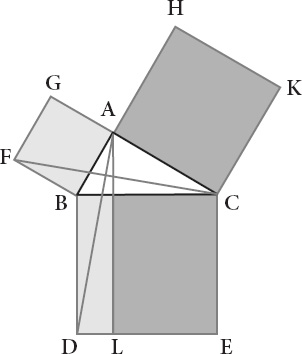
F
IGURE
VI.3.
Euclid's setup
There are three sides to a triangle and three squares in the proof. They are BDEC, which is drawn on the line BC; BFGA, on the line AB; and ACKH, on the line AC. Euclid
justifies the construction of these squares by means of his forty-sixth proposition: “On a given straight line, to describe a square.” Better because better: On a given straight line, there
exists
a square.
A single triangle has accommodated an entourage of bloated bodyguards. What now; what next?
Proposition forty-seven is the first theorem in which a masterful Euclid imposes on his readers the distinction between strategy and tactics. His tactics involve two sets of congruent triangles. They play the role of proxies. They are congruent, those proxies, and so the same. But as Euclid will show, they are also equal to squares or parts of squares. The strategy of his proof thus involves a feint toward incidental objects, followed by a sweep toward the theorem's essential identities, the axis of his attack curving like a scythe.
I
N ORDER TO
obtain the first of his proxies, Euclid drops a line from A to L, one parallel to either BD or CE. He then joins the lines AD and FC. BAC and BAG are right angles. CA and AG constitute a single straight line. Euclid's fourth axiom is in play, and so is his tenth definition (which the reader is invited to rescue from its obscurity).
But BA is also a straight line with respect to AH. And what is more, the angles DBC and FBA are equal because they are right angles.
Euclid now adds the angle ABC both to DBC and FBA. It follows that the whole angle DBA is equal to the whole angle FBC. Euclid's second common notion is now in the game and doing useful work at last.
But look: BD is equal to BC. They are sides of the same square. And FB is equal to BA, for the same reason. The triangles ABD and FBC are thus congruent by Euclid's fourth proposition.
Euclid has finished feinting; and the first half of his proof is complete.
E
UCLID NOW ESTABLISHES
a conclusion about figures that are not triangles at all. The parallelogram BDL, he argues, is twice the triangle ABD. They have the same base BD and are in the parallels BD and AL.
In justifying this assertionâthe only recondite assertion in his proofâEuclid appeals to his forty-first theorem: “If a parallelogram have the same base with a triangle, and be in the same parallels, the parallelogram is double of the triangle.”
1
By the same reasoning, the square GB is double the triangle FBC. They have the same base in FB and are in the same parallel lines FB and GC. The double of equals is equal to one another. It follows that the parallelogram BDL is equal to the square GB.
Euclid now repeats his reasoning. If AE and BK are joined, he asserts, two new congruent triangles appear in HBK and AEC. The parallelogram CL must be equal to square HC.
A farewell to those fabulous feints is in order. They have done their work. Euclid's attack is now direct; it is straightforward; and his proof proceeds by the solid, time-tested tactic of putting two and two together. The square BDEC is equal to its parts in EL and CL. But CL is equal to the square GL; and EL to the square AK. When reassembled, the square BDEC, having been divided for purposes of proof, is equal to GL and AK.
The square on the side BC is equal to the squares on the sides BA and AC.
Done.
See that, Son
?
Yes, Sir.
Attaboy.
Â
1
.
The translation of this proposition would be easier to understand were the words “in the same parallels” replaced by the words “are lying within the same parallels.” The parallelogram and the triangle, in other words, are bounded by the
same
parallel lines.
VISIBLE AND INVISIBLE PROOF
Reductio ad absurdum
, which Euclid loved so much, is one of a mathematician's finest weapons. It is a far finer gambit than any chess play: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game.
âG. H. H
ARDY
Some paint comes across directly onto the nervous system and other paint tells you the story in a long diatribe through the brain.
âF
RANCIS
B
ACON
I
N
A
NTOINE
W
ATTEAU
'
S
wonderful painting
Jupiter and Antiope
, a tense and muscular Jupiter has withdrawn Antiope's silken robe from her sleeping body, and, of course, bound by durable pigments, he does nothing more, the
poor brute forever locked where Watteau left him, lost in longing and fuming with impatience.
This is the great limitation of the Western pictorial tradition. The plane is static. Nothing moves. It is a limitation aching to be violated. In the eighteenth and nineteenth centuries, inventions appeared in which a series of stiff paper scraps would, when rapidly flipped, create a fragile illusion of real life. Adults were enchanted, children amused. There was the zoetrope, the magic lantern, the praxinoscope, the thaumatrope, the phenakistoscope, and the flip book. Praxinoscopic visionaries could see that a series of mounted scraps might one day depict Jupiter in all his massive muscular force doing something more than crouching in impatience. Whatever the unfolding that the cinema reveals, it is one prefigured in the experience that the sophisticated imagination brings to the pictorial plane itself. A great painting invites its own analytical continuation, an arrangement of two-dimensional shapes allowed during a moment of aesthetic fantasy to shed its confinement and enter into the future or the past. In commenting on John Ruskin, the art historian Kenneth Clark appealed to a superiority that allowed him “to conjure images vividly in the mind's eye.” Whatever Ruskin's superiority, it embodies a power that in part we all share, the ability in looking at a painting to wriggle out of the present and slip into the stream of time.
The analytic continuation of a great painting very often controls its aesthetic properties and so its natural critical vocabulary. Watteau's
Jupiter and Antiope
is filled with
tension
âthe obvious wordâand its arrangement of shapes unstable, if for no better reason than the discomfort Jupiter is shortly to feel in his right arm. Johannes Vermeer's
View of Delft
is, by way of contrast, serene. Projected into the future or recovered from the past, it hardly changes, the river passing into an open canal, the clouds, the reflections on the water's surface, the sandânot so much timeless as indifferent, a flow, a ripeness, too.
T
HE
ELEMENTS
IS
unusual as a mathematical treatise in that it is meticulously illustrated. For every theorem, there is a picture; and with rare exceptions, the pictures are marvels, the
Elements
providing its readers with a series of ingenious geometrical tableaus: triangles, circles, squares, rectangles, lines crossed or in parallel, the stable and familiar shapes of art and architecture, each presented in isolation, a pedagogical handmaiden to the text, the work of a masterful teacher who knew just when the confidence of his students was about to sag. It may be possible to acquire the
Elements
without once attending to its illustrations, but no one has done so.
Like Watteau's
Jupiter and Antiope
or Vermeer's
View of Delft
, there is nothing in the
Elements
that corresponds to what in life is a fluid ever-changing successionâ
those
images that yet, fresh images beget.
The illustrations are essential because they are a beginning. “Who could dispense with the figure of the triangle, [or] the circle with its centre?” David Hilbert asked in 1900. The axioms have nothing to do with it. “We do not habitually follow the chain of reasoning back to the axioms,” Hilbert observed. “On the contrary we apply, especially in first attacking a problem, a rapid, unconscious, not absolutely sure combination, trusting to a certain arithmetical feeling for the behavior of the arithmetical symbols, which we could dispense with as little in arithmetic as with the geometrical imagination in geometry.”
It is in the rich and fascinating interplay between the logical structure of his theorems and their brilliantly contrived illustrations that Euclid's art comes most alive.
Yes,
alive
; yes,
art.
Do we know whether Euclid composed his own illustrations? We do not. The manuscript trail goes cold in the Middle Ages, no more than scraps found earlier, shuffling antiquarians fingering them absently in Cairo or Baghdad and then consigning them to cedar cases. And this is another aspect of the
Elements
, the enigma of the book, the identity of its author.
E
UCLID
'
S TWENTY
-
SEVENTH
proposition affirms that if a straight line EF falling on two straight lines AB and CD
makes the alternate angles AEF and EFD equal, then AB is parallel to CD (
Figure VII.1
).
1
Some stripping of the theorem is required. A straight line EF falls on two straight lines AB and CD. Said once, it need not be said again. The three straight lines are like Somerset Maugham's three fat women of Antibes: they are there. The stripped-down theorem: if AEF is equal to EFD, then AB is parallel to CD.
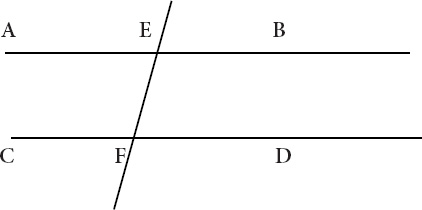
F
IGURE
VII.1.
Proposition twenty-seven
Figure VII.1
tells us no more than this: angles are equal; lines are parallel. It is monotonous. If the figure is understood as a temporal sliceâone depicting a figure frozen at one momentâmight extending it into the future reveal
something more of its inner tensions, the balance of forces leading to the theorem itself? Crouching in Watteau's oil, Jupiter might moments later be imagined pouncing, but in projecting
Figure VII.1
into the next moment, we see nothing that we have not seen before. The thing is as it was. Its angles are equal, its lines parallel.
Just where is that “rapid, unconscious, not entirely sure” visual intuition when it is needed? Needless to say,
Figure VII.1
is
not
the diagram Euclid used.
E
UCLID
'
S TWENTY
-
SEVENTH
proposition says that if AEF is equal to EFD, then AB is parallel to CD. What has been stripped down may now be stripped bare: if
P
, then
Q
. It is only when Euclid goes bone deep that he is able to observe the logical space in which his arguments and illustrations fuse completely.
Hypothetical propositions contain two propositions in
P
and
Q
; there is correspondingly a fourfold region of logical space which they may cohabit.
If P, then Q
is front to back, and
if Q, then P
is back to front. One is the converse of the other. A proposition and its converse are logically independent; they are free to go their separate ways.
If
~
P, then
~
Q
is again front to back (with ~
P
meaning “not
P
” and ~
Q
meaning “not
Q
”) and is called the inverse of
if P, then Q.
The converse and inverse of a given proposition are logically equivalent. There is no distance between them;
they say the same thing. And finally, there is
if
~
Q, then
~
P
, the contrapositive of
if P, then Q
, the coupling of conversion and inversion (rather a desperate description, now that I think about it). A proposition and its contrapositive are logically equivalent.