Understanding Computation (15 page)

>>pattern=Concatenate.new(Literal.new('a'),Literal.new('b'))=> /ab/>>pattern.matches?('a')=> false>>pattern.matches?('ab')=> true>>pattern.matches?('abc')=> false
This conversion process is recursive—Concatenate#to_nfa_designcalls#to_nfa_designon other objects—so it also
works for more deeply nested cases like the regular expressionabc, which contains two concatenations
(aconcatenated withbconcatenated withc):
>>pattern=Concatenate.new(Literal.new('a'),Concatenate.new(Literal.new('b'),Literal.new('c')))=> /abc/>>pattern.matches?('a')=> false>>pattern.matches?('ab')=> false>>pattern.matches?('abc')=> true
This is another example of a denotational semantics being
compositional
: the NFA denotation of a compound
regular expression is composed from the denotations of its
parts.
We can use a similar strategy to convert aChooseexpression into an NFA. In the simplest
case, the NFAs for the regular expressionsaandbcan
be combined to build an NFA for the regular expressiona|bby adding a new start state and using free
moves to connect it to the previous start states of the two original
machines:

Before thea|bNFA has read any input, it can use a
free move to go into either of the original machines’ start states, from which point it can
read either'a'or'b'to reach an accept state. Again, it’s just as easy to glue together any two machines by
adding a new start state and two free moves:
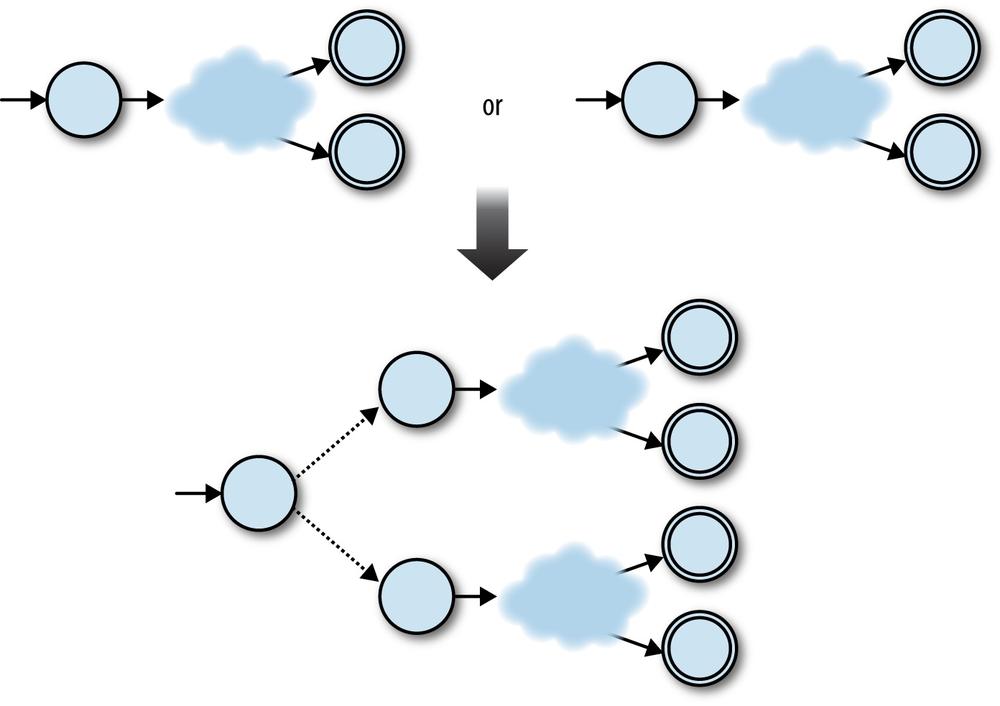
In this case, the ingredients for the combined machine are:
A new start state
All the accept states from both NFAs
All the rules from both NFAs
Two extra free moves to connect the new start state to each of the NFA’s old start
states
Again, this is easy to implement asChoose#to_nfa_design:
classChoosedefto_nfa_designfirst_nfa_design=first.to_nfa_designsecond_nfa_design=second.to_nfa_designstart_state=Object.newaccept_states=first_nfa_design.accept_states+second_nfa_design.accept_statesrules=first_nfa_design.rulebook.rules+second_nfa_design.rulebook.rulesextra_rules=[first_nfa_design,second_nfa_design].map{|nfa_design|FARule.new(start_state,nil,nfa_design.start_state)}rulebook=NFARulebook.new(rules+extra_rules)NFADesign.new(start_state,accept_states,rulebook)endend
The implementation works nicely:
>>pattern=Choose.new(Literal.new('a'),Literal.new('b'))=> /a|b/>>pattern.matches?('a')=> true>>pattern.matches?('b')=> true>>pattern.matches?('c')=> false
And finally, repetition: how can we turn an NFA that matches a
string exactly once into an NFA that matches the same string zero or
more times? We can build an NFA fora*by starting with the NFA foraand making two additions:
Add a free move from its accept state to its start state, so it can match more than
one'a'.Add a new accepting start state with a free move to the old start state, so it can
match the empty string.
Here’s how that looks:
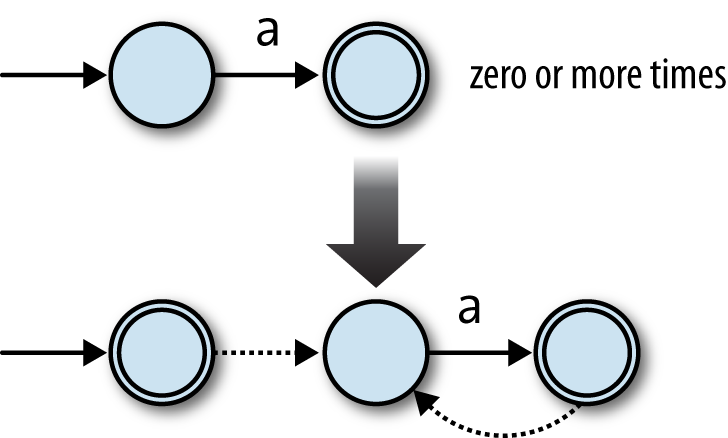
The free move from the old accept state to the old start state allows the machine to
match several times instead of just once ('aa','aaa', etc.), and the new start state allows it to match the
empty string without affecting what
other strings it can accept.
[
24
]
We can do the same for any NFA as long as we connect each old accept state to
the old start state with a free move:

This time we need:
A new start state, which is also an accept state
All the accept states from the old NFA
All the rules from the old NFA
Some extra free moves to connect each of the old NFA’s accept states to its old
start stateAnother extra free move to connect the new start state to the old start state
Let’s turn that into code:
classRepeatdefto_nfa_designpattern_nfa_design=pattern.to_nfa_designstart_state=Object.newaccept_states=pattern_nfa_design.accept_states+[start_state]rules=pattern_nfa_design.rulebook.rulesextra_rules=pattern_nfa_design.accept_states.map{|accept_state|FARule.new(accept_state,nil,pattern_nfa_design.start_state)}+[FARule.new(start_state,nil,pattern_nfa_design.start_state)]rulebook=NFARulebook.new(rules+extra_rules)NFADesign.new(start_state,accept_states,rulebook)endend