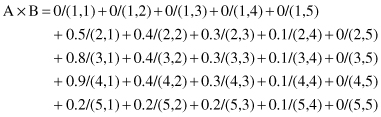Data Mining (124 page)
Authors: Mehmed Kantardzic

A graphical illustration of some of these basic concepts is given in Figure
14.4
.
Figure 14.4.
Core, support, and α-cut for fuzzy set A.
14.2 FUZZY-SET OPERATIONS
Union, intersection, and complement are the most basic operations in classic sets. Corresponding to the ordinary set operations, fuzzy sets too have operations, which were initially defined by Zadeh, the founder of the fuzzy-set theory.
The
union
of two fuzzy sets A and B is a fuzzy set C, written as C = A ∪ B or C = A
OR
B, whose MF μ
C
(x) is related to those of A and B by
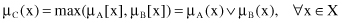
As pointed out by Zadeh, a more intuitive but equivalent definition of the union of two fuzzy sets A and B is the “smallest” fuzzy set containing both A and B. Alternatively, if D is any fuzzy set that contains both A and B, then it also contains A ∪ B.
The
intersection
of fuzzy sets can be defined analogously. The intersection of two fuzzy sets A and B is a fuzzy set C, written as C = A ∩ B or C = A
AND
B, whose MF is related to those of A and B by
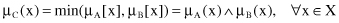
As in the case of the union of sets, it is obvious that the intersection of A and B is the “largest” fuzzy set that is contained in both A and B. This reduces to the ordinary-intersection operation if both A and B are non-fuzzy.
The
complement
of a fuzzy set A, denoted by A′, is defined by the MF as
Figure
14.5
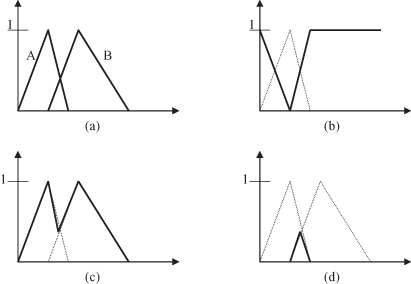
demonstrates these three basic operations: Figure
14.5
a illustrates two fuzzy sets A and B; Figure
14.5
b is the complement of A; Figure
14.5
c is the union of A and B; and Figure
14.5
d is the intersection of A and B.
Figure 14.5.
Basic operations on fuzzy sets. (a) Fuzzy sets A and B; (b) C = A’; (c) C = A ∪ B; (d) C = A ∩ B.
Let A and B be fuzzy sets in X and Y domains, respectively. The Cartesian product of A and B, denoted by A × B, is a fuzzy set in the product space X × Y with an MF
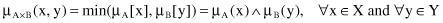
Numeric computations based on these simple fuzzy operations are illustrated through one simple example with a discrete universe of discourse S. Let S = {1, 2, 3, 4, 5} and assume that fuzzy sets A and B are given by:
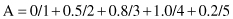
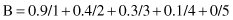
Then,
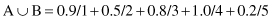
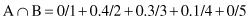
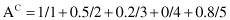
and the Cartesian product of fuzzy sets A and B is