How to Read a Paper: The Basics of Evidence-Based Medicine (15 page)
Read How to Read a Paper: The Basics of Evidence-Based Medicine Online
Authors: Trisha Greenhalgh


Another consideration is the shape of the distribution from which the data were sampled. When I was at school, my class plotted the amount of pocket money received against the number of children receiving that amount. The results formed a histogram the same shape as in
Figure 5.1
—a ‘normal’ distribution. (The term
normal
refers to the shape of the graph and is used because many biological phenomena show this pattern of distribution.) Some biological variables such as body weight show
skew
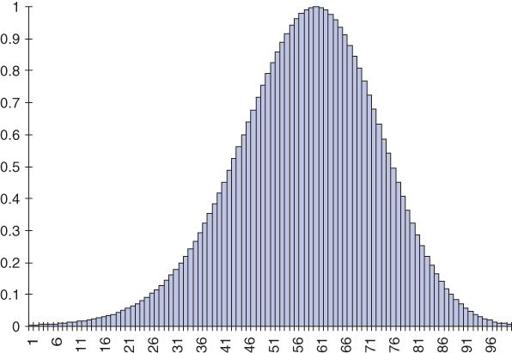
distribution, as shown in
Figure 5.2
. (
Figure 5.2
, in fact, shows a negative skew, whereas body weight would be positively skewed. The average adult male body weight is around 80 kg and people exist who are 160 kg but nobody weighs less than nothing, so the graph cannot possibly be symmetrical.)
Figure 5.1
Example of a normal curve.
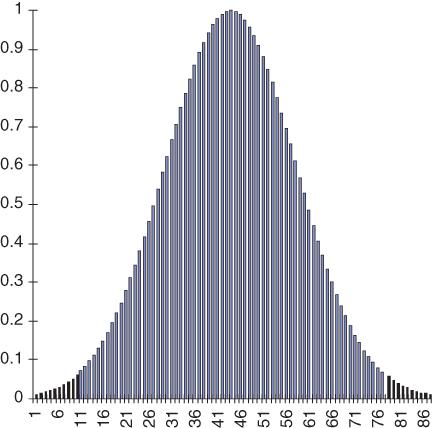
Figure 5.2
Example of a skew curve.
Non-normal (skewed) data can sometimes be
transformed
to give a normal-shape graph by plotting the logarithm of the skewed variable or performing some other mathematical transformation (such as square root or reciprocal). Some data, however, cannot be transformed into a smooth pattern, and the significance of this is discussed subsequently. Deciding whether data are normally distributed is not an academic exercise, because it will determine what type of statistical tests to use. For example, linear regression (see section ‘Correlation, regression and causation’) will give misleading results unless the points on the scatter graph form a particular distribution about the regression line—that is, the residuals (the perpendicular distance from each point to the line) should themselves be normally distributed. Transforming data to achieve a normal distribution (if this is indeed achievable) is not cheating. It simply ensures that data values are given appropriate emphasis in assessing the overall effect. Using tests based on the normal distribution to analyse non-normally distributed data is very definitely cheating.
If the statistical tests in the paper are obscure, why have the authors chosen to use them, and have they included a reference?
There sometimes seems to be an infinite number of possible statistical tests. In fact, most basic clinical studies can be analysed using a formulary of about a dozen. The rest are small-print, and should be reserved for special indications. If the paper you are reading appears to describe a standard set of data that have been collected in a standard way, but the test used is unpronounceable and not listed in a basic statistics textbook, you should smell a rat. The authors should, in such circumstances, state why they have used this test, and give a reference (with page numbers) for a definitive description of it.
Box 5.2 Tests for causation (see Reference [14])
1.
Is there evidence from true experiments in humans?
2.
Is the association strong?
3.
Is the association consistent from study to study?
4.
Is the temporal relationship appropriate (i.e. did the postulated cause precede the postulated effect)?
5.
Is there a dose–response gradient (i.e. does more of the postulated effect follow more of the postulated cause)?
6.
Does the association make epidemiological sense?
7.
Does the association make biological sense?
8.
Is the association specific?
9.
Is the association analogous to a previously proven causal association?
Have the data been analysed according to the original study protocol?
Even if you are not interested in the statistical justification, common sense should tell you why points 8 and 9 in Box 5.2 at the end of this chapter amount to serious cheating. If you trawl for long enough, you will inevitably find some category of participants who appear to have done particularly well or badly. However, each time you look to see if a particular subgroup is different from the rest you greatly increase the likelihood that you will eventually find one that appears to be so, even though the difference is entirely due to chance.
Similarly, if you play coin toss with someone, no matter how far you fall behind, there will come a time when you are one ahead. Most people would agree that to stop the game then would not be a fair way to play. So it is with research. If you make it inevitable that you will (eventually) obtain an apparently positive result you will also make it inevitable that you will be misleading yourself about the justice of your case. Terminating an intervention trial prematurely for ethical reasons when participants in one arm are faring particularly badly is different, and is discussed elsewhere [8].
Going back and raking over your data to look for ‘interesting’ results (retrospective subgroup analysis or, more colloquially, data dredging) can lead to false conclusions [9] [10]. In an early study on the use of aspirin in the prevention of stroke in predisposed patients, the results showed a significant effect in both sexes combined, and a retrospective subgroup analysis appeared to show that the effect was confined to men [11]. This conclusion led to aspirin being withheld from women for many years until the results of other studies (including a large meta-analysis [12]) showed this subgroup effect to be spurious.
This and other examples are given in a paper by Oxman and Guyatt [13], ‘A consumer’s guide to subgroup analysis', which reproduces a useful checklist for deciding whether apparent differences in subgroup response are real.
Paired data, tails and outliers
Were paired tests performed on paired data?
Students often find it difficult to decide whether to use a paired or unpaired statistical test to analyse their data. There is, in fact, no great mystery about this. If you measure something twice on each participant (e.g. lying and standing blood pressure), you will probably be interested not just in the average difference in lying versus standing blood pressure in the entire sample, but in how much each individual's blood pressure changes with position. In this situation, you have what are called
paired
data, because each measurement beforehand is paired with a measurement afterwards.
In this example, it is having the same person on both occasions that makes the pairings, but there are other possibilities (e.g. any two measurements made of bed occupancy of the same hospital ward). In these situations, it is likely that the two sets of values will be significantly correlated (e.g. my blood pressure next week is likely to be closer to my blood pressure last week than to the blood pressure of a randomly selected adult last week). In other words, we would expect two randomly selected ‘paired’ values to be closer to each other than two randomly selected ‘unpaired’ values. Unless we allow for this, by carrying out the appropriate ‘paired’ sample tests, we can end up with a biased estimate of the significance of our results.
Was a two-tailed test performed whenever the effect of an intervention could conceivably be a negative one?
The concept of a test with tails always has me thinking of devils or snakes, which I guess just reflects my aversion to statistics. In fact, the term
tail
refers to the extremes of the distribution—the dark areas in
Figure 5.1
. Let's say that graph represents the diastolic blood pressures of a group of individuals of which a random sample are about to be put on a low-sodium diet. If a low-sodium diet has a significant lowering effect on blood pressure, subsequent blood pressure measurements on these participants would be more likely to lie within the left-hand ‘tail’ of the graph. Hence, we would analyse the data with statistical tests designed to show whether unusually low readings in this patient sample were likely to have arisen by chance.
But on what grounds may we assume that a low-sodium diet could only conceivably put blood pressure down, but could never put it
up
? Even if there are valid physiological reasons why that might be the case in this particular example, it is certainly not good science always to assume that you know the
direction
of the effect that your intervention will have. A new drug intended to relieve nausea might actually exacerbate it; and an educational leaflet intended to reduce anxiety might increase it. Hence, your statistical analysis should, in general, test the hypothesis that either high
or
low values in your dataset have arisen by chance. In the language of the statisticians, this means you need a two-tailed test unless you have very convincing evidence that the difference can only be in one direction.
Were ‘outliers’ analysed with both common sense and appropriate statistical adjustments?
Unexpected results may reflect idiosyncrasies in the participant (e.g. unusual metabolism), errors in measurement (e.g. faulty equipment), errors in interpretation (e.g. misreading a meter reading), or errors in calculation (e.g. misplaced decimal points). Only the first of these is a ‘real’ result that deserves to be included in the analysis. A result that is many orders of magnitude away from the others is less likely to be genuine, but it may be. A few years ago, while doing a research project, I measured a number of different hormone levels in about 30 participants. One participant's growth hormone levels came back about a hundred times higher than everyone else's. I assumed this was a transcription error, so I moved the decimal point two places to the left. Some weeks later, I met the technician who had analysed the specimens and he asked ‘Whatever happened to that chap with acromegaly?’
Statistically correcting for outliers (e.g. to modify their effect on the overall result) is quite a sophisticated statistical manoeuvre. If you are interested, try the relevant section in your favourite statistics textbook.
Correlation, regression and causation
Has correlation been distinguished from regression, and has the correlation coefficient (‘
r
-value’) been calculated and interpreted correctly?
For many non-statisticians, the terms
correlation
and
regression
are synonymous, and refer vaguely to a mental image of a scatter graph with dots sprinkled messily along a diagonal line sprouting from the intercept of the axes. You would be right in assuming that if two things are not correlated, it will be meaningless to attempt a regression. But regression and correlation are both precise statistical terms that serve different functions [2].