How to Read a Paper: The Basics of Evidence-Based Medicine (16 page)

The
r
-value (or to give it its official name, ‘Pearson’s product–moment correlation coefficient') is among the most overused statistical instruments in the book. Strictly speaking, the
r
-value is not valid unless certain criteria, as given here, are fulfilled.

1.
The data (or, more accurately, the population from which the data are drawn) should be normally distributed. If they are not, non-parametric tests of correlation should be used instead (see
Table 5.1
).

2.
The two variables should be structurally independent (i.e. one should not be forced to vary with the other). If they are not, a paired
t
or other paired test should be used instead.

3.
Only a single pair of measurements should be made on each participant, as the measurements made on successive participants need to be statistically independent of each other if we are to end up with unbiased estimates of the population parameters of interest.

4.
Every
r
-value should be accompanied by a
p
-value, which expresses how likely an association of this strength would be to have arisen by chance (see section ‘Have ‘
p
-values’ been calculated and interpreted appropriately?’), or a confidence interval, which expresses the range within which the ‘true’
R
-value is likely to lie (see section ‘Have confidence intervals been calculated, and do the authors' conclusions reflect them?’). (Note that lower case ‘
r
’ represents the correlation coefficient of the sample, whereas upper case ‘
R
’ represents the correlation coefficient of the entire population.)

Remember, too, that even if the
r
-value is an appropriate value to calculate from a set of data, it does not tell you whether the relationship, however strong, is causal (see subsequent text).

The term
regression
refers to a mathematical
equation
that allows one variable (the
target
variable) to be predicted from another (the
independent
variable). Regression, then, implies a direction of influence, although as the next section will argue, it does not prove causality. In the case of multiple regression, a far more complex mathematical equation (which, thankfully, usually remains the secret of the computer that calculated it) allows the target variable to be predicted from two or more independent variables (often known as
covariables
).

The simplest regression equation, which you may remember from your school days, is
y
=
a
+
bx
, where
y
is the dependent variable (plotted on the vertical axis),
x
is the independent variable (plotted on the horizontal axis),
a
is the
y
-intercept and
b
is a constant. Not many biological variables can be predicted with such a simple equation. The weight of a group of people, for example, varies with their height, but not in a linear way. In the first edition of this book, I gave the example ‘I am twice as tall as my son and three times his weight, but although I am four times as tall as my newborn nephew I am much more than six times his weight’. Both son and nephew now tower over me, but the example will hold. Weight probably varies more closely with the square of someone's height than with height itself, so a quadratic rather than a linear regression would be more appropriate.

Even when you have fed sufficient height–weight data into a computer for it to calculate the regression equation that best predicts a person's weight from their height, your predictions would still be pretty poor, as weight and height are not all that closely
correlated
. There are other things that influence weight in addition to height, and we could, to illustrate the principle of multiple regression, enter data on age, sex, daily calorie intake and physical activity level into the computer and ask it how much each of these covariables contributes to the overall equation (or model).

The elementary principles described here, particularly the numbered points earlier, should help you spot whether correlation and regression are being used correctly in the paper you are reading. A more detailed discussion on the subject can be found in statistical textbooks listed at the end of this chapter [5–7], and in the fourth article in the Basic Statistics for Clinicians series [2].

Have assumptions been made about the nature and direction of causality?

Remember the ecological fallacy: just because a town has a large number of unemployed people and a very high crime rate, it does not necessarily follow that the unemployed are committing the crimes! In other words, the presence of an
association
between A and B tells you nothing at all about either the presence or the direction of causality. In order to demonstrate that A has
caused
B (rather than B causing A, or A and B both being caused by C), you need more than a correlation coefficient. Box 5.1 gives some criteria, originally developed by Sir Austin Bradford Hill [14], which should be met before assuming causality.

Probability and confidence

Have ‘
p
-values’ been calculated and interpreted appropriately?

One of the first values a student of statistics learns to calculate is the
p
-value—that is the probability that any particular outcome would have arisen by chance. Standard scientific practice, which is essentially arbitrary, usually deems a
p
-value of less than one in twenty (expressed as
p
< 0.05, and equivalent to a betting odds of twenty to one) as ‘statistically significant’, and a
p
-value of less than one in a hundred (
p
< 0.01) as ‘statistically highly significant’.

By definition, then, one chance association in twenty (this must be around one major published result per journal issue) will appear to be significant when it isn't, and one in a hundred will appear highly significant when it is really what my children call a ‘fluke’. Hence, if the researchers have made multiple comparisons, they ought to make a correction to try to allow for this. The most widely known procedure for doing this is probably the Bonferroni test (described in most standard statistical textbooks), although a reviewer of earlier editions of this book described this as ‘far too severe’ and offered several others. Rather than speculate on tests that I don't personally understand, I recommend asking a statistician's advice if the paper you are reading makes multiple comparisons.

A result in the statistically significant range (
p
< 0.05 or
p
< 0.01 depending on what you have chosen as the cutoff) suggests that the authors should reject the null hypothesis (i.e. the hypothesis that there is no real difference between two groups). But as I have argued earlier (see section ‘Were preliminary statistical questions addressed?’), a
p
-value in the non-significant range tells you that
either
there is no difference between the groups
or
there were too few participants to demonstrate such a difference if it existed. It does not tell you which.

The
p
-value has a further limitation. Guyatt and colleagues conclude thus, in the first article of their ‘Basic Statistics for Clinicians’ series on hypothesis testing using
p
-values.

Why use a single cut-off point [for statistical significance] when the choice of such a point is arbitrary? Why make the question of whether a treatment is effective a dichotomy (a yes-no decision) when it would be more appropriate to view it as a continuum?
[1].

For this, we need confidence intervals, which are considered next.

Have confidence intervals been calculated, and do the authors' conclusions reflect them?

A confidence interval, which a good statistician can calculate on the result of just about any statistical test (the
t
-test, the
r
-value, the absolute risk reduction (ARR), the number needed to treat and the sensitivity, specificity and other key features of a diagnostic test), allows you to estimate for both ‘positive’ trials (those that show a statistically significant difference between two arms of the trial) and ‘negative’ ones (those that appear to show no difference), whether the strength of the evidence is
strong
or
weak
, and whether the study is
definitive
(i.e. obviates the need for further similar studies). The calculation of confidence intervals has been covered with great clarity in the classic book ‘Statistics with Confidence’ [15], and their interpretation has been covered by Guyatt and colleagues [4].

If you repeated the same clinical trial hundreds of times, you would not obtain exactly the same result each time. But,
on average
, you would establish a particular level of difference (or lack of difference!) between the two arms of the trial. In 90% of the trials, the difference between two arms would lie within certain broad limits, and in 95% of the trials, it would lie between certain, even broader, limits.

Now, if, as is usually the case, you only conducted one trial, how do you know how close the result is to the ‘real’ difference between the groups? The answer is you don't. But by calculating, say, the 95% confidence interval around your result, you will be able to say that there is a 95% chance that the ‘real’ difference lies between these two limits. The sentence to look for in a paper should read something like this one.

In a trial of the treatment of heart failure, 33% of the patients randomised to ACE inhibitors died, whereas 38% of those randomised to hydralazine and nitrates died. The point estimate of the difference between the groups [the best single estimate of the benefit in lives saved from the use of an ACE inhibitor] is 5%. The 95% confidence interval around this difference is −1.2% to +12%.

More likely, the results would be expressed in the following shorthand.

The ACE inhibitor group had a 5% (95% CI −1.2 + 12) higher survival
.

In this particular example, the 95% confidence interval overlaps zero difference and, if we were expressing the result as a dichotomy (i.e. is the hypothesis ‘proven’ or ‘disproven’?), we would classify it as a negative trial. Yet, as Guyatt and colleagues argue, there
probably
is a real difference, and it
probably
lies closer to 5% than either −1.2% or +12%. A more useful conclusion from these results is that ‘all else being equal, an angiotensin-converting enzyme (ACE) inhibitor is probably the appropriate choice for patients with heart failure, but the strength of that inference is weak’ [4].

As section ‘Ten questions to ask about a paper that claims to validate a diagnostic or screening test’ argues, the larger the trial (or the larger the pooled results of several trials), the narrower the confidence interval—and, therefore, the more likely the result is to be definitive.

In interpreting ‘negative’ trials, one important thing you need to know is ‘would a much larger trial be likely to show a significant benefit?’. To answer this question, look at the
upper
95% confidence interval of the result. There is only one chance in forty (i.e. a 2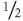
% chance, as the other 2
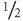% of extreme results will lie below the
lower
95% confidence interval) that the real result will be this much or more. Now ask yourself: ‘Would this level of difference be
clinically
significant?’, and if it wouldn't, you can classify the trial as not only negative but also definitive. If, on the other hand, the upper 95% confidence interval represented a clinically significant level of difference between the groups, the trial may be negative but it is also non-definitive.