How to Read a Paper: The Basics of Evidence-Based Medicine (24 page)

Now, if I carry out a diagnostic test for anaemia, the serum ferritin level, the result will usually make the diagnosis of anaemia either more or less likely. A moderately reduced serum ferritin level (between 18 and 45 µg/l) has a likelihood ratio of 3, so the chances of a patient with this result having iron-deficiency anaemia is generally calculated as 0.05 × 3—or 0.15 (15%). This value is known as the
post-test probability of the serum ferritin test
. (Strictly speaking, likelihood ratios should be used on odds rather than on probabilities, but the simpler method shown here gives a good approximation when the pre-test probability is low. In this example, a pre-test probability of 5% is equal to a pre-test odds of 0.05/0.95 or 0.053; a positive test with a likelihood ratio of 3 gives a post-test odds of 0.158, which is equal to a post-test probability of 14%) [17].

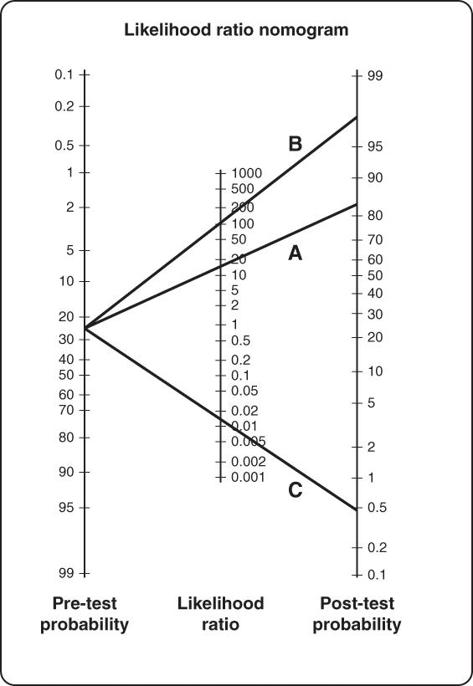
Figure 8.4
shows a nomogram, adapted by Sackett and colleagues from an original paper by Fagan [18], for working out post-test probabilities when the pre-test probability (prevalence) and likelihood ratio for the test are known. The lines A, B and C, drawn from a pre-test probability of 25% (the prevalence of smoking amongst British adults) are, respectively, the trajectories through likelihood ratios of 15, 100 and 0.015—three different (and all somewhat old) tests for detecting whether someone is a smoker [19]. Actually, test C detects whether the person is a
non-smoker
, as a positive result in this test leads to a post-test probability of only 0.5%.

In summary, as I said at the beginning of this chapter, you can go a long way with diagnostic tests without referring to likelihood ratios. I avoided them myself for years. But if you put aside an afternoon to get to grips with this aspect of clinical epidemiology, I predict that your time will have been well spent.

Clinical prediction rules

In the previous section, I took you through a rather heavy-going example of the PSA test, and concluded that there is no single, clear-cut value that reliably distinguishes ‘normal’ from ‘abnormal’. This is why the recommended approach to assessing a man's risk of prostate cancer is a combination of several tests, including the overall clinical assessment and a digital rectal examination [16].

More generally, you can probably see why, in general, clinicians tend to use a combination of several different diagnostic tests (including their clinical examination, blood tests, X-rays, etc.) to build up a picture of what is wrong with the patient. Whilst any one test has a fuzzy boundary between normal and abnormal, combining them may sharpen the diagnostic focus. So, for example, a woman who presents with a breast lump tends to be offered three different tests, none of which is especially useful when used in isolation: fine needle aspiration, X-ray (mammogram) and ultrasound [20]. More recently, scholars have begun a debate as to whether computerised mammography reading increases the accuracy of this triple combination further [21].

Figure 8.4
Using likelihood ratios to calculating the post-test probability of someone being a smoker.

This general principle—do several tests and combine them—is a longstanding rule of thumb in clinical practice, recently updated in a more structured form by Falk and Fahey [22]. By following large cohorts of patients with particular symptoms, and carefully recording the findings of clinical examinations and diagnostic tests in all of them, we can come up with numerical estimates of the chance of a person having (or going on to develop) disease X in the presence of symptom A, physical sign B, diagnostic test C, and so on—or any combination of these. Interest in—and research into—clinical prediction rules has been growing rapidly in recent years, partly because the growth of information technology means that very large numbers of patients can be entered onto online databases by clinicians in different centres.

As Falk and Fahey point out, there are three stages in the development of a clinical prediction rule. First, the rule must be developed by establishing the independent and combined effect of explanatory variables such as symptoms, signs, or diagnostic tests on the diagnosis. Second, these explanatory variables should be assessed in different populations. And third, there should be an impact analysis—ideally a randomised trial that measures the impact of applying the rule in a clinical setting in terms of patient outcome, clinician behaviour, resource use, and so on.

For examples of how clinical prediction rules can help us work through some of the knottiest diagnostic challenges in health care, see these papers on how to predict whether a head-injured child should be sent for a computed tomography (CT) scan [23], whether someone with early arthritis is developing rheumatoid arthritis [24], whether someone taking anticoagulants is of sufficiently low risk of stroke to be able to discontinue them [25], and which combinations of tests best predict whether an acutely ill child has anything serious wrong with him or her [26].

References

1
World Health Organization. Definition and diagnosis of diabetes mellitus and intermediate hyperglycemia: report of a WHO/IDF consultation. Geneva: World Health Organization, 2006:1–50.

2
Andersson D, Lundblad E, Svärdsudd K. A model for early diagnosis of type 2 diabetes mellitus in primary health care.
Diabetic Medicine
1993;
10
(2):167–73.

3
Friderichsen B, Maunsbach M. Glycosuric tests should not be employed in population screenings for NIDDM.
Journal of Public Health
1997;
19
(1):55–60.

4
Bennett C, Guo M, Dharmage S. HbA1c as a screening tool for detection of type 2 diabetes: a systematic review.
Diabetic Medicine
2007;
24
(4):333–43.

5
Lu ZX, Walker KZ, O'Dea K, et al. A1C for screening and diagnosis of type 2 diabetes in routine clinical practice.
Diabetes Care
2010;
33
(4):817–9.

6
Jaeschke R, Guyatt G, Sackett DL, et al. Users' guides to the medical literature: III. How to use an article about a diagnostic test. A. Are the results of the study valid?
JAMA: The Journal of the American Medical Association—US Edition
1994;
271
(5):389–91.

7
Guyatt G, Bass E, Brill-Edwards P, et al. Users' guides to the medical literature: III. How to use an article about a diagnostic test. B. What are the results and will they help me in caring for my patients?
JAMA: The Journal of American Medical Association
1994;
271
(9):703–7.

8
Guyatt G, Sackett D, Haynes B. Evaluating diagnostic tests.
Clinical epidemiology: how to do clinical practice research
2006;
424
:273–322.

9
Mant D. Testing a test: three critical steps.
Oxford General Practice Series
1995;
28
:183.

10
Lucas NP, Macaskill P, Irwig L, et al. The development of a quality appraisal tool for studies of diagnostic reliability (QAREL).
Journal of Clinical Epidemiology
2010;
63
(8):854–61.

11
Lu Y, Dendukuri N, Schiller I, et al. A Bayesian approach to simultaneously adjusting for verification and reference standard bias in diagnostic test studies.
Statistics in Medicine
2010;
29
(24):2532–43.

12
Altman DG, Machin D, Bryant TN, et al.
Statistics with confidence: confidence intervals and statistical guidelines
. Bristol: BMJ Books, 2000.

13
Appel LJ, Miller ER, Charleston J. Improving the measurement of blood pressure: is it time for regulated standards?
Annals of Internal Medicine
. 2011;
154
(12):838–9.

14
Sackett DL, Haynes RB, Tugwell P.
Clinical epidemiology: a basic science for clinical medicine
. Boston: Little, Brown and Company, 1985.

15
Holmström B, Johansson M, Bergh A, et al. Prostate specific antigen for early detection of prostate cancer: longitudinal study.
BMJ: British Medical Journal
2009;
339
:b3537.

16
Barry M, Denberg T, Owens D, et al. Screening for prostate cancer: a guidance statement from the Clinical Guidelines Committee of the American College of Physicians.
Annals of Internal Medicine
2013;
158
:761–9.

17
Guyatt GH, Patterson C, Ali M, et al. Diagnosis of iron-deficiency anemia in the elderly.
The American Journal of Medicine
1990;
88
(3):205–9.

18
Fagan TJ. Letter: nomogram for Bayes theorem.
The New England Journal of Medicine
1975;
293
(5):257.

19
Moore A, McQuay H, Muir Gray J. How good is that test—using the result.
Bandolier. Oxford
1996;
3
(6):6–8.

20
Houssami N, Irwig L. Likelihood ratios for clinical examination, mammography, ultrasound and fine needle biopsy in women with breast problems.
The Breast
1998;
7
(2):85–9.

21
Giger ML. Update on the potential of computer-aided diagnosis for breast cancer.
Future Oncology
2010;
6
(1):1–4.

22
Falk G, Fahey T. Clinical prediction rules.
BMJ: British Medical Journal
2009;
339
:b2899.

23
Maguire JL, Boutis K, Uleryk EM, et al. Should a head-injured child receive a head CT scan? A systematic review of clinical prediction rules.
Pediatrics
2009;
124
(1):e145–54.

24
Kuriya B, Cheng CK, Chen HM, et al. Validation of a prediction rule for development of rheumatoid arthritis in patients with early undifferentiated arthritis.
Annals of the Rheumatic Diseases
2009;
68
(9):1482–5.

25
Rodger MA, Kahn SR, Wells PS, et al. Identifying unprovoked thromboembolism patients at low risk for recurrence who can discontinue anticoagulant therapy.
Canadian Medical Association Journal
2008;
179
(5):417–26.

26
Verbakel JY, Van den Bruel A, Thompson M, et al. How well do clinical prediction rules perform in identifying serious infections in acutely ill children across an international network of ambulatory care datasets?
BMC Medicine
2013;
11
(1):10.

Chapter 9

Papers that summarise other papers (systematic reviews and meta-analyses)

When is a review systematic?

Remember the essays you used to write when you first started college? You would mooch round the library, browsing through the indexes of books and journals. When you came across a paragraph that looked relevant you copied it out, and if anything you found did not fit in with the theory you were proposing, you left it out. This, more or less, constitutes the
journalistic
review—an overview of primary studies that have not been identified or analysed in a systematic (i.e. standardised and objective) way. Journalists get paid according to how much they write rather than how much they read or how critically they process it, which explains why most of the ‘new scientific breakthroughs’ you read in your newspaper today will probably be discredited before the month is out. A common variant of the journalistic review is the invited review, written when an editor asks one of his or her friends to pen a piece, and summed up by this fabulous title: ‘The invited review? Or, my field, from my standpoint, written by me using only my data and my ideas, and citing only my publications’ [1]!