How to Read a Paper: The Basics of Evidence-Based Medicine (26 page)

Methodological shortcomings that invalidate the results of trials are often generic (i.e. they are independent of the subject matter of the study; see Appendix 1), but there may also be certain methodological features that distinguish between good, medium and poor quality in a particular field. Hence, one of the tasks of a systematic reviewer is to draw up a list of criteria, including both generic and particular aspects of quality, against which to judge each trial. In theory, a composite numerical score could be calculated which would reflect ‘overall methodological quality’. In reality, however, care should be taken in developing such scores as there is no gold standard for the ‘true’ methodological quality of a trial and such composite scores may prove neither valid nor reliable in practice. If you're interested in reading more about the science of developing and applying quality criteria to studies as part of a systematic review, see the latest edition of the Cochrane Reviewers' Handbook [12].

Question Four: How sensitive are the results to the way the review has been performed?

If you don't understand what this question means, look up the tongue-in-cheek paper by Counsell and colleagues [13] some years ago in the
British Medical Journal
, which ‘proved’ an entirely spurious relationship between the result of shaking a dice and the outcome of an acute stroke. The authors report a series of artificial dice-rolling experiments in which red, white and green dice, respectively, represented different therapies for acute stroke.

Overall, the ‘trials’ showed no significant benefit from the three therapies. However, the simulation of a number of perfectly plausible events in the process of meta-analysis—such as the exclusion of several of the ‘negative’ trials through publication bias (see section ‘Randomised controlled trials’), a subgroup analysis that excluded data on red dice therapy (because, on looking back at the results, red dice appeared to be harmful), and other, essentially arbitrary, exclusions on the grounds of ‘methodological quality’—led to an apparently highly significant benefit of ‘dice therapy’ in acute stroke.

You cannot, of course, cure anyone of a stroke by rolling a dice, but if these simulated results pertained to a genuine medical controversy (such as which postmenopausal women would be best advised to take hormone replacement therapy or whether breech babies should routinely be delivered by Caesarean section), how would you spot these subtle biases? The answer is you need to work through the what-ifs. What if the authors of the systematic review had changed the inclusion criteria? What if they had excluded unpublished studies? What if their ‘quality weightings’ had been assigned differently? What if trials of lower methodological quality had been included (or excluded)? What if all the unaccounted-for patients in a trial were assumed to have died (or been cured)?

An exploration of what-ifs is known as a
sensitivity analysis
. If you find that fiddling with the data like this in various ways makes little or no difference to the review's overall results, you can assume that the review's conclusions are relatively robust. If, however, the key findings disappear when any of the what-ifs changes, the conclusions should be expressed far more cautiously and you should hesitate before changing your practice in the light of them.

Box 9.3 Assigning weight to trials in a systematic review

Each trial should be evaluated in terms of its:

• methodological quality
  —that is, extent to which the design and conduct are likely to have prevented systematic errors (bias) (see section ‘Was systematic bias avoided or minimised?’);
  
• precision
  —that is, a measure of the likelihood of random errors (usually depicted as the width of the confidence interval around the result);
  
• external validity
  —that is, the extent to which the results are generalisable or applicable to a particular target population.
  

(Additional aspects of ‘quality’ such as scientific importance, clinical importance and literary quality are rightly given great weight by peer reviewers and journal editors, but are less relevant to the systematic reviewer once the question to be addressed has been defined.)

Question Five: Have the numerical results been interpreted with common sense and due regard to the broader aspects of the problem?

As the next section shows, it is easy to be phased by the figures and graphs in a systematic review. But any numerical result, however precise, accurate, ‘significant’, or otherwise incontrovertible, must be placed in the context of the painfully simple and (often) frustratingly general question that the review addressed. The clinician must decide how (if at all) this numerical result,
whether significant or not
, should influence the care of an individual patient.

A particularly important feature to consider when undertaking or appraising a systematic review is the external validity of included trials (see Box 9.3). A trial may be of high methodological quality and have a precise and numerically impressive result, but it may, for example, have been conducted on participants under the age of 60, and hence may not apply at all to people over 75 for good physiological reasons. The inclusion in systematic reviews of irrelevant studies is guaranteed to lead to absurdities and reduce the credibility of secondary research.

Meta-analysis for the non-statistician

If I had to pick one term that exemplifies the fear and loathing felt by so many students, clinicians and consumers towards EBM, that word would be ‘meta-analysis’. The meta-analysis, defined as
a statistical synthesis of the numerical results of several trials that all addressed the same question
, is the statisticians' chance to pull a double whammy on you. First, they frighten you with all the statistical tests in the individual papers, and then they use a whole new battery of tests to produce a new set of odds ratios, confidence intervals and values for significance.

As I confessed in Chapter 5, I too tend to go into panic mode at the sight of ratios, square root signs and half-forgotten Greek letters. But before you consign meta-analysis to the set of specialised techniques that you will never understand, remember two things. First, the meta-analyst may wear an anorak but he or she is
on your side
. A good meta-analysis is often easier for the non-statistician to understand than the stack of primary research papers from which it was derived, for reasons I am about to explain. Second, the underlying statistical principles used for meta-analysis are the same as the ones for any other data analysis—it's just that some of the numbers are bigger.

The first task of the meta-analyst, after following the preliminary steps for systematic review in
Figure 9.1
, is to decide which out of all the various outcome measures chosen by the authors of the primary studies is the best one (or ones) to use in the overall synthesis. In trials of a particular chemotherapy regimen for breast cancer, for example, some authors will have published cumulative mortality figures (i.e. the total number of people who have died to date) at cut-off points of 3 and 12 months, whereas other trials will have published 6-month, 12-month and 5-year cumulative mortality. The meta-analyst might decide to concentrate on 12-month mortality because this result can be easily extracted from all the papers. He or she may, however, decide that 3-month mortality is a clinically important end-point, and would need to write to the authors of the remaining trials asking for the raw data from which to calculate these figures.

In addition to crunching the numbers, part of the meta-analyst's job description is to tabulate relevant information on the inclusion criteria, sample size, baseline patient characteristics, withdrawal (‘drop-out’) rate and results of primary and secondary end-points of all the studies included. If this task has been performed properly, you will be able to compare both the methods and the results of two trials whose authors wrote up their research in different ways. Although such tables are often visually daunting, they save you having to plough through the methods sections of each paper and compare one author's tabulated results with another author's pie chart or histogram.

These days, the results of meta-analyses tend to be presented in a fairly standard form. This is partly because meta-analysts often use computer software to do the calculations for them (see the latest edition of the Cochrane Reviewers' handbook for an up-to-date menu of options [12]), and most such software packages include a standard graphics tool that presents results as illustrated in
Figure 9.2
. I have reproduced (with the authors' permission) this pictorial representation (colloquially known as a
forest plot
or
blobbogram
) of the pooled odds ratios of eight randomised controlled trials of therapy for depression. Each of these eight studies had compared a group receiving cognitive behaviour therapy (CBT) with a control group that received no active treatment and in whom pharmacotherapy (PHA—i.e. drug treatment) was discontinued [14]. The primary (main) outcome in this meta-analysis was relapse within 1 year.

Figure 9.2
Forest plot showing long-term effects of cognitive behaviour therapy (CBT) compared with no active treatment and discontinuation of pharmacotherapy (PHA).

Source: Cuijpers et al. [14]. Reproduced with permission from BMJ.

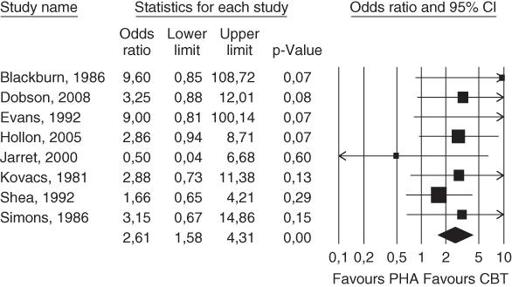
The eight trials, each represented by the surname of the first author and the year that paper was published (e.g. ‘Blackburn 1986’) are listed, one below the other on the left hand side of the figure. The horizontal line corresponding to each trial shows the likelihood of relapse by 1 year in patients randomised to CBT compared to patients randomised to PHA. The ‘blob’ in the middle of each line is the point estimate of the difference between the groups (the best single estimate of the benefit in improved relapse rate by offering CBT rather than PHA), and the width of the line represents the 95% confidence interval of this estimate (see section ‘Have confidence intervals been calculated, and do the authors' conclusions reflect them?’). The key vertical line to look at, known as the
line of no effect
, is the one marking the relative risk (RR) of 1.0. Note that if the horizontal line for any trial does not cross the line of no effect, there is a 95% chance that there is a ‘real’ difference between the groups.

As sections ‘Were preliminary statistical questions addressed?’ and ‘Probability and confidence’ argued, if the confidence interval of the result (the horizontal line)
does
cross the line of no effect (i.e. the vertical line at RR = 1.0), that can mean
either
that there is no significant difference between the treatments,
and/or
that the sample size was too small to allow us to be confident where the true result lies. The various individual studies give point estimates of the odds ratio of CBT compared to PHA (of between 0.5 and 9.6), and the confidence intervals of some studies are so wide that they don't even fit on the graph.

Now, here comes the fun of meta-analysis. Look at the tiny diamond below all the horizontal lines. This represents the
pooled
data from all eight trials (overall RR CBT:PHA = 2.61, meaning that CBT has 2.61 times the odds of preventing relapse), with a new, much narrower, confidence interval of this RR (1.58–4.31). Because the diamond does not overlap the line of no effect, we can say that there is a statistically significant difference between the two treatments in terms of the primary end-point (relapse of depression in the first year). Now, in this example, seven of the eight trials suggested a benefit from CBT, but in none of them was the sample size large enough for that finding to be statistically significant.

Note, however, that this neat little diamond does
not
mean that you should offer CBT to every patient with depression. It has a much more limited meaning—that the
average
patient in the trials presented in this meta-analysis is likely to benefit in terms of the primary outcome (relapse of depression within a year) if they receive CBT. The choice of treatment should, of course, take into account how the patient feels about embarking on a course of CBT (see Chapter 16) and also on the relative merits of this therapy compared to
other
treatments for depression. The paper from which
Figure 9.2
is taken also described a second meta-analysis that showed no significant difference between CBT and continuing antidepressant therapy, suggesting, perhaps, that patients who prefer not to have CBT may do just as well by continuing to take their tablets [14].