In Pursuit of the Unknown (34 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

The pace of progress, and the heights to which humans could ascend, began to increase rapidly. In 1903 Orville and Wilbur Wright made the first powered flight in an aeroplane. The first airline, DELAG (
Deutsche Luftschiffahrts-Aktiengesellschaft
), began operations in 1910, flying passengers from Frankfurt to Baden-Baden and Düsseldorf using airships made by the Zeppelin Corporation. By 1914 the St PetersburgâTampa Airboat Line was flying passengers commercially between the two Florida cities, a journey that took 23 minutes in Tony Jannus's flying boat. Commercial air travel quickly became commonplace, and jet aircraft arrived: the De Havilland Comet began regular flights in 1952, but metal fatigue caused several crashes, and the Boeing 707 became the market leader from its launch in 1958.
Ordinary individuals could now routinely be found at an altitude of 8 kilometres, their limit to this day, at least until Virgin Galactic starts low-orbital flights. Military flights and experimental aircraft rose to greater heights. Space flight, hitherto the dream of a few visionaries, started to become a plausible proposition. In 1961 the Soviet cosmonaut Yuri Gagarin made the first manned orbit of the Earth in
Vostok 1
. In 1969 NASA's
Apollo 11
mission landed two American astronauts, Neil Armstrong and Buzz Aldrin, on the Moon. The space shuttle began operational flights in 1982, and while budget constraints prevented it achieving the original aims â a reusable vehicle with a rapid turnaround â it became one of the workhorses of low-orbit spaceflight, along with Russia's
Soyuz
spacecraft.
Atlantis
has now made the final flight of the space shuttle programme, but new vehicles are being planned, mainly by private companies. Europe, India, China, and Japan have their own space programmes and agencies.
This literal ascent of humanity has changed our view of who we are and where we live â the main reason why âEarth' now means a blueâwhite globe. Those colours hold a clue to our newfound ability to fly. The blue is water, and the white is water vapour in the form of clouds. Earth is a water world, with oceans, seas, rivers, lakes. What water does best is to
flow
, often to places where it's not wanted. The flow might be rain dripping from a roof or the mighty torrent of a waterfall. It can be gentle and smooth, or rough and turbulent â the steady flow of the Nile across what would otherwise be desert, or the frothy white water of its six cataracts.
It was the patterns formed by water, or more generally any moving fluid, that attracted the attention of mathematicians in the nineteenth century, when they derived the first equations for fluid flow. The vital fluid for flight is less visible than water, but just as ubiquitous: air. The flow of air is more complex mathematically, because air can be compressed. By modifying their equations so that they applied to a compressible fluid, mathematicians initiated the science that would eventually get the Age of Flight off the ground: aerodynamics. Early pioneers might fly by rule of thumb, but commercial airliners and the space shuttle fly because engineers have done the calculations that make them safe and reliable (barring occasional accidents). Aircraft design requires a deep understanding of the mathematics of fluid flow. And the pioneer of fluid dynamics was the renowned mathematician Leonhard Euler, who died in the year the Montgolfiers made their first balloon flight.
There are few areas of mathematics towards which the prolific Euler did not turn his attention. It has been suggested that one reason for his prodigious and versatile output was politics, or more precisely, its avoidance. He worked in Russia for many years, at the court of Catherine the Great, and an effective way to avoid being caught up in political intrigue, with potentially disastrous consequences, was to be so busy with his mathematics that no one would believe he had any time to spare for politics. If this is what he was doing, we have Catherine's court to thank for many wonderful discoveries. But I'm inclined to think that Euler was prolific because he had that sort of mind. He created huge quantities of mathematics because he could do no other.
There were predecessors. Archimedes studied the stability of floating bodies over 2200 years ago. In 1738 the Dutch mathematician Daniel Bernoulli published
Hydrodynamica
(âHydrodynamics'), containing the principle that fluids flow faster in regions where the pressure is lower. Bernoulli's principle is often invoked today to explain why aircraft can fly: the wing is shaped so that the air flows faster across the top surface, lowering the pressure and creating lift. This explanation is a bit too simplistic, and many other factors are involved in flight, but it does illustrate the close relationship between basic mathematical principles and practical aircraft design. Bernoulli embodied his principle in an algebraic equation relating velocity and pressure in an incompressible fluid.
In 1757 Euler turned his fertile mind to fluid flow, publishing an article âPrincipes généraux du mouvement des fluides' (General principles of the movement of fluids) in the
Memoirs of the Berlin Academy
. It was the first serious attempt to model fluid flow using a partial differential equation. To keep the problem within reasonable bounds, Euler made some simplifying assumptions: in particular, he assumed the fluid was incompressible, like water rather than air, and had zero viscosity â no stickiness. These assumptions allowed him to find some solutions, but they also made his equations rather unrealistic. Euler's equation is still in use today for some types of problem, but on the whole it is too simple to be of much practical use.
Two scientists came up with a more realistic equation. Claude-Louis Navier was a French engineer and physicist; George Gabriel Stokes was an Irish mathematician and physicist. Navier derived a system of partial differential equations for the flow of a viscous fluid in 1822; Stokes started publishing on the topic twenty years later. The resulting model of fluid flow is now called the NavierâStokes equation (often the plural is used because the equation is stated in terms of a vector, so it has several
components). This equation is so accurate that nowadays engineers often use computer solutions instead of performing physical tests in wind tunnels. This technique, known as computational fluid dynamics (CFD), is now standard in any problem involving fluid flow: the aerodynamics of the space shuttle, the design of Formula 1 racing cars and everyday road cars, and blood circulating through the human body or an artificial heart.
There are two ways to look at the geometry of a fluid. One is to follow the movements of individual tiny particles of fluid and see where they go. The other is to focus on the velocities of such particles: how fast, and in which direction, they are moving at any instant. The two are intimately related, but the relationship is difficult to disentangle except in numerical approximations. One of the great insights of Euler, Navier, and Stokes was the realisation that everything looks a lot simpler in terms of the velocities. The flow of a fluid is best understood in terms of a velocity field: a mathematical description of how the velocity varies from point to point in space and from instant to instant in time. So Euler, Navier, and Stokes wrote down equations describing the velocity field. The actual flow patterns of the fluid can then be calculated, at least to a good approximation.
The NavierâStokes equation looks like this:
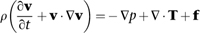
where
Ï
is the density of the fluid,
v
is its velocity field,
p
is pressure,
T
determines the stresses, and
f
represents body forces â forces that act throughout the entire region, not just at its surface. The dot is an operation on vectors, and â is an expression in partial derivatives, namely
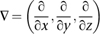
The equation is derived from basic physics. As with the wave equation, a crucial first step is to apply Newton's second law of motion to relate the movement of a fluid particle to the forces that act on it. The main force is elastic stress, and this has two main constituents: frictional forces caused by the viscosity of the fluid, and the effects of pressure, either positive (compression) or negative (rarefaction). There are also body forces, which stem from the acceleration of the fluid particle itself. Combining all this information leads to the NavierâStokes equation, which can be seen as a
statement of the law of conservation of momentum in this particular context. The underlying physics is impeccable, and the model is realistic enough to include most of the significant factors; this is why it fits reality so well. Like all of the traditional equations of classical mathematical physics it is a continuum model: it assumes that the fluid is infinitely divisible.
This is perhaps the main place where the NavierâStokes equation potentially loses touch with reality, but the discrepancy shows up only when the motion involves rapid changes on the scale of individual molecules. Such small-scale motions are important in one vital context: turbulence. If you turn on a tap and let the water flow out slowly, it arrives in a smooth trickle. Turn the tap on full, however, and you often get a surging, frothy, foaming gush of water. Similar frothy flows occur in rapids on a river. This effect is known as turbulence, and those of us who fly regularly are well aware of its effects when it occurs in air. It feels as though the aircraft is driving along a very bumpy road.
Solving the NavierâStokes equation is hard. Until really fast computers were invented, it was so hard that mathematicians were reduced to short cuts and approximations. But when you think about what a real fluid can do, it
ought
to be hard. You only have to look at water flowing in a stream, or waves breaking on a beach, to see that fluids can flow in extremely complex ways. There are ripples and eddies, wave patterns and whirlpools, and fascinating structures like the Severn bore, a wall of water that races up the estuary of the River Severn in south-west England when the tide comes in. The patterns of fluid flow have been the source of innumerable mathematical investigations, yet one of the biggest and most basic questions in the area remains unanswered: is there a mathematical guarantee that solutions of the NavierâStokes equation actually
exist
, valid for all future time? There is a million-dollar prize for anyone who can solve it, one of the seven Clay Institute Millennium Prize problems, chosen to represent the most important unsolved mathematical problems of our age. The answer is âyes' in two-dimensional flow, but no one knows for three-dimensional flow.
Despite this, the NavierâStokes equation provides a useful model of turbulent flow because molecules are extremely small. Turbulent vortices a few millimetres across already capture many of the main features of turbulence, whereas a molecule is far smaller, so a continuum model remains appropriate. The main problem that turbulence causes is practical: it makes it virtually impossible to solve the NavierâStokes equation numerically, because a computer can't handle infinitely complex
calculations. Numerical solutions of partial differential equations use a grid, dividing space into discrete regions and time into discrete intervals. To capture the vast range of scales on which turbulence operates â its big vortices, middle-sized ones, right down to the millimetre-scale ones â you need an impossibly fine computational grid. For this reason, engineers often use statistical models of turbulence instead.
The NavierâStokes equation has revolutionised modern transport. Perhaps its greatest influence is on the design of passenger aircraft, because not only do these have to fly efficiently, but they have to
fly
, stably and reliably. Ship design also benefits from the equation, because water is a fluid. But even ordinary household cars are now designed on aerodynamic principles, not just because it makes them look sleek and cool, but because efficient fuel consumption relies on minimising drag caused by the flow of air past the vehicle. One way to reduce your carbon footprint is to drive an aerodynamically efficient car. Of course there are other ways, ranging from smaller, slower cars to electric motors, or just driving less. Some of the big improvements in fuel consumption figures have come from improved engine technology, some from better aerodynamics.