In Pursuit of the Unknown (33 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

Fig 41
The 64 basic patterns from which any block of 8 Ã 8 pixels can be obtained.
This step paves the way to step four, a second exploitation of the deficiencies of human vision. We are more sensitive to variations in brightness (or colour) over large regions than we are to closely spaced variations. So the patterns in the figure can be recorded less accurately as the spacing of the stripes becomes finer. This compresses the data further. The fifth and final step uses a âHuffman code' to express the list of strengths of the 64 basic patterns in a more efficient manner.
Every time you take a digital image using JPEG, the electronics in your camera does all of these things, except perhaps step one. (Professionals are
now moving over to RAW files, which record the actual data without compression, together with the usual âmetadata' such as date, time, exposure, and so on. Files in this format take up more memory, but memory gets bigger and cheaper by the month, so that no longer matters.) A trained eye can spot the loss of image quality created by JPEG compression when the quantity of data is reduced to about 10% of the original, and an untrained eye can see it clearly by the time the file size is down to 2â3%. So your camera can record about ten times as many images on a memory card, compared with the raw image data, before anyone other than an expert would notice.
Because of applications like these, Fourier analysis has become a reflex among engineers and scientists, but for some purposes the technique has one major fault: sines and cosines go on forever. Fourier's method runs into problems when it tries to represent a compact signal. It takes huge numbers of sines and cosines to mimic a localised blip. The problem is not getting the basic shape of the blip right, but making everything outside the blip equal to zero. You have to kill off the infinitely long rippling tails of all those sines and cosines, which you do by adding on even more high-frequency sines and cosines in a desperate effort to cancel out the unwanted junk. So the Fourier transform is hopeless for blip-like signals: the transformed version is more complicated, and needs more data to describe it, than the original.
What saves the day is the generality of Fourier's method. Sines and cosines work because they satisfy one simple condition: they are mathematically independent. Formally, this means that they are
orthogonal:
in an abstract but meaningful sense, they are at right angles to each other. This is where Euler's trick, eventually rediscovered by Fourier, comes in. Multiplying two of the basic sinusoidal waveforms together and integrating over one period is a way to measure how closely related they are. If this number is large, they are very similar; if it is zero (the condition for orthogonality), they are independent. Fourier analysis works because its basic waveforms are both orthogonal and complete: they are independent and there are enough of them to represent any signal if they are suitably superposed. In effect, they provide a coordinate system on the space of all signals, just like the usual three axes of ordinary space. The main new feature is that we now have
infinitely many
axes: one for each basic waveform. But this doesn't cause many difficulties mathematically,
once you get used to it. It just means you have to work with infinite series instead of finite sums, and worry a little about when the series converge.
Even in finite-dimensional spaces, there are many different coordinate systems; the axes can be rotated to point in new directions, for example. It's not surprising to find that in an infinite-dimensional space of signals, there are alternative coordinate systems that differ wildly from Fourier's. One of the most important discoveries in the whole area, in recent years, is a new coordinate system in which the basic waveforms are confined to a limited region of space. They are called wavelets, and they can represent blips very efficiently because they
are
blips.
Only recently did anyone realise that blip-like Fourier analysis was possible. Getting started is straightforward: choose a particular shape of blip, the mother wavelet (
Figure 42
). Then generate daughter wavelets (and granddaughters, great-granddaughters, whatever) by sliding the mother wavelet sideways into various positions, and expanding her or compressing her by a change of scale. In the same way, Fourier's basic sine and cosine curves are âmother sinelets', and the higher-frequency sines and cosines are daughters. Being periodic, these curves cannot be blip-like.
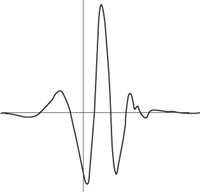
Fig 42
Daubechies wavelet.
Wavelets are designed to describe bliplike data efficiently. Moreover, because the daughter and granddaughter wavelets are just rescaled versions of mother, it is possible to focus on particular levels of detail. If you don't want to see small-scale structure, you just remove all the great-granddaughter wavelets from the wavelet transform. To represent a leopard by wavelets, you need a few big ones to get the body right, smaller ones for the eyes, nose, and of course the spots, and very tiny ones for individual hairs. To compress the data representing the leopard, you might decide that the individual hairs don't matter, so you just remove those particular component wavelets. The great thing is, the image still
looks like a leopard, and it still has spots. If you try to do this with the Fourier transform of a leopard then the list of components is huge, it's not clear which items you should remove, and you probably won't recognise the result as a leopard.
All very well and good, but what shape should the mother wavelet be? For a long time nobody could work that out, or even show that a good shape exists. But in the early 1980s geophysicist Jean Morlet and mathematical physicist Alexander Grossmann found the first suitable mother wavelet. In 1985 Yves Meyer found a better mother wavelet, and in 1987 Ingrid Daubechies, a mathematician at Bell Laboratories, blew the whole field wide open. Although the previous mother wavelets looked suitably bliplike, they all had a very tiny mathematical tail that wiggled off to infinity. Daubechies found a mother wavelet with no tail at all: outside some interval, mother was always exactly zero â a genuine blip, confined entirely to a finite region of space.
The bliplike features of wavelets make them especially good for compressing images. One of their first large-scale practical uses was to store fingerprints, and the customer was the Federal Bureau of Investigation. The FBI's fingerprint database contains 300 million records, each of eight fingerprints and two thumbprints, which were originally stored as inked impressions on paper cards. This is not a convenient storage medium, so the records have been modernised by digitising the images and storing the results on a computer. Obvious advantages include being able to mount a rapid automated search for prints that match those found at the scene of a crime.
The computer file for each fingerprint card is 10 megabytes long: 80 million binary digits. So the entire archive occupies 3000 terabytes of memory: 24 quadrillion binary digits. To make matters worse, the number of new sets of fingerprints grows by 30,000 every day, so the storage requirement would grow by 2.4 trillion binary digits every day. The FBI sensibly decided that they needed some method for data compression. JPEG wasn't suitable, for various reasons, so in 2002 the FBI decided to develop a new system of compression using wavelets, the wavelet/scalar quantization (WSQ) method. WSQ reduces the data to 5% of its size by removing fine detail throughout the image. This is irrelevant to the eye's ability, as well as a computer's, to recognise the fingerprint.
There are also many recent applications of wavelets to medical imaging. Hospitals now employ several different kinds of scanner, which
assemble two-dimensional cross-sections of the human body or important organs such as the brain. The techniques include CT (computerised tomography), PET (positron emission tomography), and MRI (magnetic resonance imaging). In tomography, the machine observes the total tissue density, or a similar quantity, in a single direction through the body, rather like what you would see from a fixed position if all the tissue were to become slightly transparent. A two-dimensional picture can be reconstructed by applying some clever mathematics to a whole series of such âprojections', taken at many different angles. In CT, each projection requires an X-ray exposure, so there are good reasons to limit the amount of data acquired. In all such scanning methods, less data takes less time to acquire, so more patients can use the same amount of equipment. On the other hand, good images need more data so that the reconstruction method can work more effectively. Wavelets provide a compromise, in which reducing the amount of data leads to equally acceptable images. By taking a wavelet transform, removing unwanted components, and âdetransforming' back to an image again, a poor image can be smoothed and cleaned up. Wavelets also improve the strategies by which the scanners acquire their data in the first place.
In fact, wavelets are turning up almost everywhere. Researchers in areas as wide apart as geophysics and electrical engineering are taking them on board and putting them to work in their own fields. Ronald Coifman and Victor Wickerhauser have used them to remove unwanted noise from recordings: a recent triumph was a performance of Brahms playing one of his own Hungarian Dances. It was originally recorded on a wax cylinder in 1889, which partially melted; it was re-recorded on to a 78 rpm disc. Coifman started from a radio broadcast of the disc, by which time the music was virtually inaudible amid the surrounding noise. After wavelet cleansing, you could hear what Brahms was playing â not perfectly, but at least it was audible. It's an impressive track record for an idea that first arose in the physics of heat flow 200 years ago, and was rejected for publication.
| 10 | The ascent of humanity |
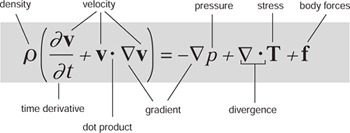
It's Newton's second law of motion in disguise. The left-hand side is the acceleration of a small region of fluid. The right-hand side is the forces that act on it: pressure, stress, and internal body forces.
It provides a really accurate way to calculate how fluids move. This is a key feature of innumerable scientific and technological problems.
Modern passenger jets, fast and quiet submarines, Formula 1 racing cars that stay on the track at high speeds, and medical advances on blood flow in veins and arteries. Computer methods for solving the equations, known as computational fluid dynamics (CFD), are widely used by engineers to improve technology in such areas.
S
een from space, the Earth is a beautiful glowing blue-and-white sphere with patches of green and brown, quite unlike any other planet in the Solar System â or any of the 500-plus planets now known to be circling other stars, for that matter. The very word âEarth' instantly brings this image to mind. Yet a little over fifty years ago, the almost universal image for the same word would have been a handful of dirt, earth in the gardening sense. Before the twentieth century, people looked at the sky and wondered about the stars and planets, but they did so from ground level. Human flight was nothing more than a dream, the subject of myths and legends. Hardly anyone thought about travelling to another world.
A few intrepid pioneers began the slow climb into the sky. The Chinese were the first. Around 500
BC
L
u
Ban invented a wooden bird, which might have been a primitive glider. In 559
AD
the upstart Gao Yang strapped Yuan Huangtou, the emperor's son, to a kite â against his will â to spy on the enemy from above. Yuan survived the experience but was later executed. With the seventeeth-century discovery of hydrogen the urge to fly spread to Europe, inspiring a few brave individuals to ascend into the lower reaches of Earth's atmosphere in balloons. Hydrogen is explosive, and in 1783 the French brothers Joseph-Michel and Jacques-Ãtienne Montgolfier gave a public demonstration of their new and much safer idea, the hot-air balloon â first with an unmanned test flight, then with Ãtienne as pilot.