Más rápido que la velocidad de la luz (4 page)

Es una cosmovisión cuyos ecos resuenan en toda nuestra cultura. En verdad, no nos gusta lo cualitativo, especialmente cuando se trata de cuestiones de dinero. Preferimos definir una unidad monetaria y después expresar el valor de cualquier cosa como un número que indica cuántas veces ese valor contiene la unidad.

Más aún, la definición de unidades permite reunir el rigor cuantitativo de las matemáticas (es decir, de los números) y la realidad física. La unidad representa una cantidad patrón de cierta magnitud; el número expresa la cantidad exacta que queremos describir.

Así, el concepto de kilogramo nos permite expresar con precisión qué queremos decir cuando hablamos de siete kilogramos de ananás, y también nos permite expresar cuánto cuestan. Nuestra civilización no sería la que conocemos si no existieran, en combinación, el concepto de unidad y el concepto de número. Aunque nos proclamemos poéticos, amamos el rigor cuantitativo y no podemos vivir sin él: en mi vida he conocido
muy
poca gente anarquista a tal extremo, a pesar de haberme topado con algunos individuos muy singulares.

La filosofía de la vida impregna nuestra concepción del espacio y del tiempo. El espacio se define mediante una unidad de longitud, por ejemplo, el metro. Conociéndola, puedo decir que un elefante está a 315 metros de mí, lo cual significa que la distancia que me separa de él es 315 veces esa unidad rígida, el metro. De ese modo, podemos expresar con rigor la ubicación del elefante.

Si quiero hacer un mapa de una región de la superficie terrestre, recurro a una estructura espacial bidimensional. Defino dos direcciones ortogonales, por ejemplo, la dirección norte-sur y la dirección este-oeste. Con ellas, puedo especificar con exactitud la posición de cualquier objeto con respecto a mí mediante dos números: la distancia que lo separa de mí en la dirección este-oeste y la distancia que lo separa de mí en la dirección norte-sur. Ese marco bidimensional define cualquier posición con exactitud. Nuestra obsesión por saber con precisión la ubicación de todas las cosas ha encontrado su expresión más perfecta en los sistemas de posicionamiento global, denominados gps
{global positioning system).
Con ellos se puede conocer la ubicación de cualquier punto de la superficie terrestre con una precisión que raya en lo absurdo.

Desde luego, todos estos sistemas son producto de convenciones. Los aborígenes australianos conciben el mapa de su territorio como versos de una canción. Para ellos, la idea de Australia no se expresa mediante una correspondencia biunívoca entre puntos del territorio y pares de números que son las coordenadas de esos puntos. Más bien, su tierra es un conjunto de múltiples líneas tortuosas que se entrecruzan, a lo largo de las cuales surge una determinada canción. Cada canción cuenta lo que sucedió en el curso de ese sendero; por lo general, es un mito con personajes animales humanizados, una fábula con sus meandros, plena de significado emotivo.

Los versos de la canción crean una maraña compleja, de modo que un punto no puede representarse mediante un único par de números; en semejante concepción no sólo importa dónde está cada uno (según nuestra concepción), sino también de dónde procede y, en última instancia, importa la totalidad del sendero recorrido antes y la del que se recorrerá después. Lo que para nosotros es un punto único, para esos aborígenes engendra una diversidad infinita, pues ese punto puede formar parte de muchos versos que se entrecruzan. Inevitablemente, esa manera de pensar el mundo genera una idea de la propiedad que no tiene cabida en nuestra cultura. Allí, los individuos heredan cantares en lugar de parcelas de tierra. Nadie puede construir un sistema de posicionamiento global que funcione en un espacio de canciones.

No obstante, Australia existe y los cantares de sus aborígenes indican que, en buena medida, cualquier descripción del espacio es una cuestión de elección y de convenciones. Nosotros optamos por vivir en un espacio rígido y exacto compuesto por conjuntos de puntos, el espacio newtoniano (que algunos también llaman euclidiano).

Las mismas consideraciones se pueden aplicar al tiempo. Un reloj es nada más que un objeto que cambia a un ritmo regular: algo que "hace tictac". El tictac define la unidad de tiempo, y la unidad de tiempo nos permite especificar la duración exacta de cualquier acontecimiento mediante un número. Nuestra definición del ritmo "regular" de cambio es una cuestión de convención. Sin embargo, como ocurre con muchas convenciones, no es algo puramente antojadizo, pues nos permite describir la realidad física que nos rodea de manera simple y precisa.

Tenemos una confianza tan grande en nuestra capacidad para calcular duraciones que, desde la época de Newton, el propio flujo del tiempo se nos presenta como algo uniforme y absoluto. Uniforme por definición y absoluto porque... ¿por qué habrían de discrepar distintos observadores sobre el momento en que ocurrió un suceso determinado?

No hay razón alguna para que discrepen. Sin embargo, en la época en que Einstein tuvo el sueño de las vacas, había ya una crisis en ciernes. El sueño era premonitorio: la rígida concepción del tiempo y el espacio absolutos estaba a punto de desmoronarse.

Una noche tempestuosa, las vacas que ya habían aparecido en el sueño de Einstein empiezan a mostrar síntomas inequívocos de locura. Sin motivo alguno, comienzan a moverse por la pradera a una velocidad muy próxima a la de la luz, afectadas tal vez por una extraña cepa del mal de la vaca loca, activada por la descarga eléctrica que recibieron.

Al oír la estampida, el granjero sale al campo con una linterna, pero las vacas se sosiegan al verlo y se apiñan en un extremo del terreno. Sin embargo, apenas el haz de la linterna enfoca a los animales, éstos comienzan a alejarse del granjero a una velocidad inconcebible, cada vez más cercana a la de la luz. El granjero se pregunta si, al fin y al cabo, no estarán en celo.

Pero también se formula otra pregunta. Acaba de enfocar un haz de luz sobre un grupo de vacas que se alejan de él a una velocidad muy próxima a la de la luz. Si es que las vacas prácticamente alcanzan a la luz, ¿no verán que el haz de la linterna se detiene? Sería algo realmente insólito, traten de imaginarlo. ¿Existe acaso la luz estacionaria?

A fin de responder a una pregunta tan aguda, el granjero le pide a Cornelia, una de las vacas más inteligentes del rebaño, que le informe lo que ve mientras corre junto al rayo de luz. Ella le contesta que no observa nada fuera de lo común: el haz de luz de la linterna se parece a cualquier otro rayo de luz. Es más, Cornelia se muestra muy servicial y, para asegurarse de lo que dice, procura medir la velocidad de la luz con los medios a su alcance, los relojes y varillas que lleva consigo. Su informe es por demás extraño: según ella, las cosas suceden a su alrededor como es habitual, es decir, la velocidad de la luz con respecto a ella es de 300.000 km/seg.

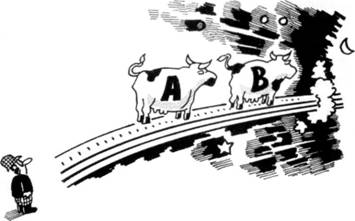
Llegado a este punto, es el granjero quien se siente irritado con Cornelia. Totalmente convencido ahora de que esa vaca proviene de un rebaño inglés, decide pedirles a otras dos vacas que midan la velocidad del haz de su linterna. Pero las circunstancias han cambiado y las vacas, menos ágiles, avanzan más lentamente que las otras. Las elegidas por el granjero se mueven a 100.000 km/seg y 200.000 km/seg con respecto a él. Para evitar confusiones con los tontos nombres de las vacas, llamémoslas vaca A y vaca B (véase la figura 3).

Puesto que el granjero ve que el haz de luz se propaga a 300.000 km/seg, espera que esas dos vacas más sensatas le devuelvan los siguientes resultados: para la vaca A, la velocidad del haz debería ser de 200.000 km/seg (es decir, 300.000 km/seg menos 100.000 km/seg); para la vaca B, la velocidad del haz debería ser de 100.000 km/seg (300.000 km/seg menos 200.000 km/seg). Al fin y al cabo, se trata de un cálculo aritmético muy simple que todos aprendimos en la escuela: las velocidades se suman o se restan (según su dirección relativa). De modo que, para obtener la velocidad del rayo de luz con respecto a cada vaca, basta con restar la velocidad de la vaca de la velocidad de la luz. ¿Estamos de acuerdo? ¿O, como habíamos sospechado desde un principio, nos han engañado los gruñones profesores de física que tuvimos que soportar?

Lamentablemente, según nuestra percepción habitual del espacio y el tiempo, los profesores de física deberían tener razón. Si dos automóviles parten de un mismo sitio siguiendo un camino rectilíneo y llevan respectivamente una velocidad de 100 km/hora y 200 km/hora, cuando mi reloj indique que ha transcurrido una hora, el primer vehículo habrá recorrido 100 km y el segundo, 200 km. ¿Cuál es la velocidad del automóvil más rápido con respecto al más lento?

Pues bien, al cabo de una hora, el automóvil más rápido ha recorrido 100 km más que el lento, es decir, 200 km menos 100 km. De modo que su velocidad con respecto al más lento es 100 km/hora. Todo es muy lógico: se restan las distancias y, como el tiempo transcurrido es el mismo, se restan las velocidades. ¿Acaso una operación tan sencilla podría dar origen a una polémica?

Análogamente, si un rayo de luz se propaga a 300.000 km/seg y hay dos vacas que se alejan de mí a 100.000 km/seg o 200.000 km/seg respectivamente, esas vacas deberían ver que el haz de luz avanza a 200.000 km/seg y 100.000 km/seg respectivamente.

Sin embargo, una vez más, las vacas dan una respuesta inesperada. ¡Las dos sostienen que la velocidad del haz con respecto a ellas es de 300.000 km/seg!

Respuestas que no sólo contradicen la lógica del granjero sino que parecen contradecirse entre sí.

¿Debemos creerles a las vacas? ¿O, por el contrario, debemos creerles a los profesores de física? Sucede, sin embargo, que el experimento concreto nos obliga a creerles a las vacas, lo que nos plantea un verdadero dilema. ¿Hubo algún error en el razonamiento que seguimos para llegar a la conclusión de que había que restar las velocidades? Según lo que hemos dicho hasta ahora, lo que observaron las vacas no tiene sentido.

Tal era, más o menos, el enigma que se les presentaba a los hombres de ciencia a fines del siglo XIX. Los experimentos que respaldaban los resultados obtenidos por las vacas se conocen hoy como experimentos de Michelson-Morley y establecían empíricamente que la velocidad de luz era constante cualquiera fuera la velocidad o estado de movimiento del observador. Si camino por el pasillo de un tren en movimiento, mi velocidad con respecto al andén es la suma de mi velocidad con respecto al tren más la velocidad del tren. Michelson y Morley descubrieron que la luz emitida desde la tierra en movimiento seguía siendo la misma. En algún sentido, se podría decir que descubrieron que 1 + 1 = 1 en unidades de velocidad de la luz. Fueron experimentos que sumieron a la física en el desconcierto, porque su resultado era ilógico y contradecía el
evidente
dogma lógico de que las velocidades siempre se suman o se restan.

La teoría especial de la relatividad formulada por Einstein resolvió el enigma aunque su autor no tenía conocimiento de los experimentos de Michelson y Morley cuando la propuso. Probablemente le debía más a su sueño de las vacas que a los experimentos. Por consiguiente, vamos a analizar la solución de Einstein basándonos en las vacas.

Volvamos a solicitar los servicios de Cornelia y pidámosle que se quede junto al granjero. Cuando el granjero emite el haz de luz, Cornelia se lanza en su persecución a 200.000 km/seg. El granjero, claro está, ve que la luz se propaga a 300.000 km/seg. Por consiguiente, al cabo de un segundo observa que el haz está a 300.000 km de distancia y también ve que Cornelia se halla a 200.000 km. En tal situación,
deduce
que Cornelia ve el haz de luz 100.000 km más adelante y, puesto que ha transcurrido un segundo, infiere que Cornelia debe observar que la velocidad del rayo de luz es de 100.000 km/seg (véase la figura 4).

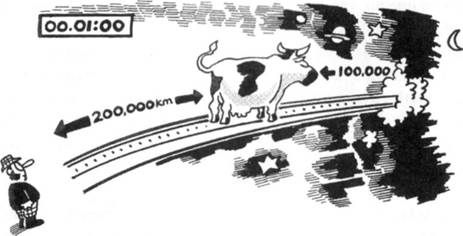
No obstante, cuando le pide que mida la velocidad de la luz, Cornelia sigue diciendo que es de 300.000 km/seg. ¿Dónde está el error?

Llegado a este punto, Einstein demostró su genio y su coraje: tuvo la audacia de sugerir que tal vez el tiempo no era el mismo para todos, que la contradicción podía explicarse suponiendo que tal vez para el granjero había transcurrido un segundo mientras que para la vaca sólo había transcurrido un tercio de segundo. Si las cosas fueran así, Cornelia habría visto, en efecto, el rayo de luz 100.000 km más adelante, pero al dividir esa distancia por el tiempo transcurrido para ella, habría obtenido el resultado de 300.000 km/seg (véase la figura 5). En otras palabras, si el tiempo transcurre más lentamente para los observadores que están en movimiento, no habría dificultad en explicar por qué todos concuerdan en el mismo valor para la velocidad de la luz contradiciendo lo que cabe esperar cuando se restan las velocidades.