Mathematics and the Real World (18 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

19. EVERYTHING YOU WANTED TO KNOW ABOUT INFINITESIMAL CALCULUS AND DIFFERENTIAL EQUATIONS
We will now present the concepts underlying the mathematics of differential and integral calculus (also known as infinitesimal calculus, namely, the calculus of small terms) and differential equations. No knowledge of or background in mathematics is required to understand these ideas, but it is worth investing a little effort and exercising a little patience to absorb the mathematical symbols that will appear here (alternatively, the reader can ignore the symbols and skip the technical part of the presentation).
In daily life we come across quantities that vary with time, for example, the position of a moving vehicle, the price of an article, or the temperature outside. In mathematics it is customary to notate the variable as a function, for example,
x
(
t
), where the variable
t
relates to time, and for every
t
, that is, at time
t
, the value of
x
(
t
) gives the position of the vehicle, the price of the article, or the outside temperature, as the case may be.
In addition to the function itself, we may be interested in the
rate of change
of the function. In the example of the moving vehicle, the rate of change in the vehicle's position measures its velocity. Where the function describes the price level in an economy, the rate of change measures inflation. The rate of change of a function is itself a function. That is because, for example, the speed of the vehicle can also change with time. In mathematics, the function that describes the rate of change is called the
derivative
of the original function and is denoted by
x
′. (Leibniz proposed giving the derivative the notation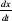 and that notation is still used today. It is important to note that this is purely notation and does not represent a division of one quantity by another.)
and that notation is still used today. It is important to note that this is purely notation and does not represent a division of one quantity by another.)
As the derivative is also a function, we can look at its rate of change as well. This would therefore be the derivative of a derivative, or in mathematical terminology, the
second derivative
of the original function, and it is written as
x
″. The second derivative can also be seen in terms of daily life. In the case of the moving vehicle, the first derivative gives the velocity; hence, the second derivative gives the rate of change of the velocity, that is, the rate of acceleration. In the example of prices, the first derivative gives the rate of inflation, and the second derivative gives the rate of change of inflation.
We could continue and define third, fourth, and higher derivatives. Sometimes these also can be interpreted in terms related to the meaning of the original function. The following is a quote from a speech by the American president Richard Nixon during the election campaign in 1972:
“The rate of increase of inflation is declining.”
He was using the third derivative. If the function we are analyzing defines prices, then its derivative shows the rate of inflation, the second derivative is the rate of change of inflation, and the meaning of President Nixon's statement is that the third derivative of the price function is negative. That was the first time, wrote the mathematician Hugo Rossi in an article in 1996, that a president used the third derivative to get reelected.
We said that no knowledge of or skill in mathematical techniques is required to understand the concepts we have described. It is sufficient to
grasp that the rate of change of a variable, such as speed, can itself change, and that is called the derivative. As we will soon see, these concepts, the derived function and higher derivatives, constitute the basis of the development of the connection between mathematics and nature. To enable the use of these concepts required the development of calculus, that is, efficient ways of calculating the rates of change, the derivatives, of functions. Vice versa, when the rate of change or the derivative is known, a method has to be found to calculate the original function. This function is called the
integral
. This branch of mathematics, calculus, was developed independently by Newton in England and by Leibniz in Germany. To understand it, knowledge of mathematical techniques was necessary, but the technical details of how to calculate derivatives and integrals are of concern mainly to researchers and those who use mathematics (and students!). To understand what is written in this section, those technical details are not at all important. We will give examples of such calculations further on. These were important for the corroboration of Newton's theory. We will just observe that the first sparks of calculus can be seen in the exhaustion method of Eudoxus and were significantly improved by Archimedes (see sections 7 and 10). Archimedes's improvement included the concept of the limit of geometric figures whose areas are easy to calculate. That limit is precisely the integral as defined by Newton and Leibniz. They took one step further, however, and generalized the method to calculate derivatives, a previously unknown mathematical concept. They raised the method to the level of mathematical rules by which derivatives and integrals can be calculated relatively simply. Both Newton and Leibniz applied the knowledge of their forebears, methods of calculating areas and slopes of tangents to specific instances, calculations that had been performed by many contemporary and earlier mathematicians, including famous figures such as Fermat, Descartes, Wallis, Barrow, and others. The contribution of Newton and Leibniz was to raise calculus from a collection of examples to the level of a general mathematical theory.
These parallel developments in England and Germany did not take place entirely peacefully, without discord between the two men, discord that enveloped the whole world of mathematics and included mutual allegations
of stealing ideas and plagiarism. Newton was the first to start developing calculus, but because of his excessive mistrust, he did not publish his findings for many years, and when he did, they did not make for easy reading and understanding. Leibniz did publish his calculus in a much clearer fashion and in Europe was credited with being the discoverer of the system (as we noted, the notation above, still in current use, was that proposed by Leibniz). Newton, in contrast, created a mathematical concept that he called fluxion, which described the instantaneous change in a function. Newton went on the attack and accused Leibniz of stealing the idea. The truth is not completely clear. It appears that in the initial stages Leibniz came across a very early version of the concept and that was sufficient, for a genius such as he was, to develop the theory independently. In any event, Leibniz denied that his work was based on an early connection with Newton or Newton's work and even demanded that the Royal Society appoint a committee to investigate Newton's accusations. A committee was appointed, and after several months of investigation it declared in favor of Newton and did not absolve Leibniz of the accusation of plagiarizing the idea from Newton. It is not clear whether this finding was affected by the fact that at that time Newton was the president of the Royal Society.
This is an appropriate point to give a brief description of Gottfried Wilhelm von Leibniz, Newton's “competitor” in the development of calculus. Leibniz was born in 1646 in Leipzig, Saxony, to a family involved in issues of law and morality. From an early age Leibniz had access to the well-stocked library of his father, who was a professor of moral philosophy, close to what today is called social science. His father died when Gottfried was a young boy. The library introduced the young Leibniz to classical Greek literature, including Aristotle's ideas on morality and philosophy, which made a very deep impression on him. He was educated by his mother's family—her father was a professor of law. From his youth Leibniz was attracted to legal topics and completed a doctoral thesis on the subject when he was twenty, but he was not awarded the degree because he was found to lack experience of life and to be too young to hold such a
title. He therefore left Leipzig and went to the University of Altdorf, where he quickly completed his doctorate in mathematics. He rejected an offer to remain as a professor at that university and in 1667 chose to work in the employ of Baron Christian von Boyneburg, who in the course of time became a close friend. In 1676 Leibniz moved to Hanover to serve the Duke of Hanover, and in due course he was appointed as the official historian of the Boyneburg family. Leibniz contributed greatly to mathematics in various fields, as we will see below, but he was not only a great scientist but also one of the greatest philosophers of all time. He died in Hanover in 1716.
Calculus has many uses in different fields, but the main reason for Newton's developing it was that it helped him solve differential equations—the tool he devised to express laws of nature—thus enabling him to use the laws of nature he had discovered. How to solve differential equations is a subject for mathematicians and those who use mathematics, but to understand what those equations are does not require a mathematical education, and certainly there is no reason to be deterred from continuing to read about them.
Since the dawn of the development of mathematics, mathematicians have tried to develop systems that would help them calculate an unknown quantity from the data available. Thus, Thales of Miletus calculated the height of the Great Pyramid in Egypt by means of the distance from the center of the pyramid and the angle at which the top of the pyramid was seen. Thus, the Babylonians calculated the length of the hypotenuse of
many
right-angled triangles using the known lengths of the other two sides. The Greeks had already formulated a general rule for calculating the length of the hypotenuse of such triangles, given the lengths of the other two sides, Pythogoras's theorem, and hence could calculate the length of the hypotenuse of
any
right-angled triangle. Presenting the connection between the unknown quantity and the data by means of an equation began only in the sixteenth century. The sign = to indicate equality was proposed by Robert Recorde, an Oxford University professor, in a book dated 1557. Since then
we write equations, which generally describe situations in real life, and use mathematical techniques to solve them. The equations we are most familiar with relate to numbers. Thus the equation
a
2
+ b
2
=
x
2
describes the calculation to obtain the length of the hypotenuse using Pythagoras's theorem, with
x
representing the length of the hypotenuse that we wish to obtain. Another well-known equation is the quadratic equation of the form
ax
2
+
bx
+
c
= 0. In school we are taught how to find the value of the unknown
x
. Sometimes there is one solution, sometimes two, and sometimes none.
Newton studied a new type of equation that does not relate to unknown numbers but rather to unknown functions and their derivatives. Today these are referred to as
differential equations
. (The actual term came into use long after Newton.) The idea is that we write a mathematical equation that gives the relation between functions and their derivatives, and we do not look for solutions in the form of numbers but the functions that satisfy the equations. An example of such an equation is:
mx
″ = –
kx
,
where the unknown is not a number, as we are used to, but a function
x(t)
. The equation can be described in words. It says that the second derivative multiplied by the number
m
is equal to the negative of the function itself multiplied by the number
k
(for the description of the equation, it is not important what
k
and
m
stand for). Sometimes additional conditions may exist that the solution must satisfy, for example, it may be specified that
x
(0) = 0. Mathematicians learn how to solve such equations. Sometimes there is just one solution, sometimes there are many, and sometimes, none. In day-to-day life the reader does not generally need to know the technique for solving differential equations, unless he or she is an engineer or a physicist using mathematics of this sort or is still a student.
20. NEWTON'S LAWS
Newton developed calculus for the purpose of giving a mathematical expression for motion in nature. In fact, his laws are formulated by differential equations. His was a remarkable achievement from various aspects. First, the contribution to physics itself. This was the first time that the same rules were applied to describe earthly and celestial motion. This conflicted with the Aristotelian approach, which was still followed in the seventeenth century. Even more impressive, however, was the use of the new mathematics of differential equations both to formulate the laws and to draw conclusions. We will briefly review the link between the new mathematics and the laws of nature.