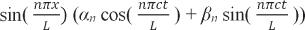Mathematics and the Real World (21 page)

Early versions of differential equations describing waves were first suggested by Leonhard Euler (1707–1783) in 1734 and by Jean D’Alembert (1717–1783) in 1743. The breakthrough in the understanding of waves in general, and the vibrations of a taut string in particular, came in 1746 and 1748, when D’Alembert and then Euler published different solutions to the equation. It eventually transpired that the two solutions were in fact the same solution in different forms. For the sake of completeness we will give the equation itself:

∂
_tt
u
(
x
,
t
) =
c
²
∂
_xx
u
(
x
,
t
)

In ordinary language this says that the acceleration of the height of the wave according to time changes in proportion to the speed at which the rate of change of the height of the wave changes at the location where it is measured.

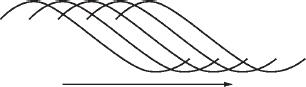
When the solutions to this equation were being studied, a surprising link was found with discoveries made by the Greeks, of course with no mathematical explanation, regarding the length of a piece of string and the note it produces when it is plucked. Without going into the technical details, we will just state that the relevant solutions of the equation describing the vibrations of a piece of string of length
L
, whose ends are fixed and unmoving, are a mixture of the sine and cosine functions that we have already encountered and that were known to the Greeks. Again for completeness, we set out a general form of solutions:

There is an infinite number of solutions, as for every natural number
n
(and for all coefficients
α
_n
and
β
_n
) the formula provides a particular solution. It can be proved mathematically that every solution of the equation will be the sum of such particular solutions. The formula itself will not interest readers for whom mathematics and its use is not their profession, but two conclusions drawn from it are related directly both to the distant past and to future developments as follows.

Note that the length
L
of the string appears in the above expressions only in the denominator. The practical significance of this mathematical fact is that when the length of the string is halved, the frequency of the vibrations (the speed at which the sine and cosine functions change) is doubled. Thus, with a delay of some two thousand years, mathematics solved the mystery of the source of the finding dating back to Pythagoras, that when the length of the string is shortened by a half, the note it produces rises by exactly a full octave. The string equation connects a full octave, which the ear can identify naturally, with doubling the speed of vibration of the string. In a similar fashion, it is possible to obtain other findings from Pythagoras's time regarding the pitch of a note and the speed of vibration of the string.

Moreover, the equation shows that the vibration of the string consists of the sum of the vibrations shown in the formula for every value of
n
equal to 1, 2, 3, and so on. These vibrations have a “clean” frequency given by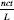
for natural
n
. These frequencies are called
natural
, or
characteristic
, frequencies of the string. They will play a central role in the modern description of nature, which we will present in the
next chapter
.

23. ON THE PERCEPTION OF SCIENCE IN MODERN TIMES

Following the huge strides taken in the development and progress in understanding the world, a modern philosophical approach took shape with regard to how science operates and how nature is understood. We will summarize that philosophy very briefly. First, mathematics occupied its rightful position in the center of the stage. No scientific finding was considered understandable unless it was supported by mathematics that described it both qualitatively and quantitatively. Second, the requirement that mathematical principles explaining the findings must reflect some sort of purpose was abandoned. The very fact that a law of nature can be described by a simple and elegant mathematical description constitutes a purpose. The description can be in the form of an equation that nature “solves,” or in the form of a “purpose,” for example, to minimize a certain quantity, such as minimizing the time a process takes or minimizing effort. Newton's contribution showed that a special, new mathematics can be developed that is appropriate for the description and analysis of natural phenomena that can be measured, and he thus cleared the path for the search of new mathematical systems to describe the laws of nature.

The empirical approach developed by Galileo Galilei in Italy and Francis Bacon in England (according to which the mathematical developments must be initiated based on experiments) has been adopted, but the predictions provided by mathematics would not be acceptable unless backed up by the results of experiments. In all aspects of the essence of mathematics and the link between mathematics and nature, despite the fact that the Aristotelian search for a purpose as the basis for all natural phenomena was abandoned, the new philosophy adopted Aristotle's formalistic attitude to mathematics (see section 11). The philosophy that developed in the early modern age still holds today, with certain refinements that we will discuss in the
next chapter
.

What can an electric current be useful for? • Is the universe paved with gears? • Are mathematics and physics one and the same? • How did the axiom of parallels affect the theory of relativity? • Who discovered the formula
E
=
mc
²
? • How can you bend light beams? • Are we actually waves? • How do elementary particles group together? • Are humans made of strings? • How many dimensions do we live in?

24. ELECTRICITY AND MAGNETISM

In the middle of the nineteenth century there was a dramatic development in the use of mathematics to describe the world. It came in the wake of results of experiments in electricity and magnetism. The mathematical explanations of these discoveries led both to further surprising revelations and to a revolution in the approach to the mathematical description of nature. In a certain sense, mathematics that describes physics became physics itself. In this section we will briefly review the experimental discoveries that resulted in that revolution.

Static electricity and magnetism were known in the times of the ancient Greeks and ancient Chinese, and possibly even earlier. Thales of Miletus knew that when amber is rubbed with a cloth, the amber attracts light objects. Today we understand that the rubbing generates static electricity that causes the attraction. The word
electricity
comes from the Greek word for amber. Magnetism was also a known phenomenon, and the word
magnet
was taken from the town Magnesia in Turkey, part of Asia Minor, which was then under the Greeks. The Greeks knew that an iron bar suspended from a cord settles in a north-south direction. Compasses based on that property were already in use in the eleventh century. In the spirit of the Greek tradition, however, no experiments were performed to study those phenomena. Throughout ancient times it was thought that magnetism and electricity were totally unrelated.

In the sixteenth century, following the scientific revolution of the modern era led by Galileo, Francis Bacon, and their contemporaries, scientists began performing controlled experiments to study and understand different natural phenomena, including magnetism and static electricity. Among the pioneers in this field was the British physicist William Gilbert (1540–1603), who carried out controlled experiments and was the first to discover that magnets have two poles, north and south. Like poles repel each other, while unlike poles attract each other. Gilbert also found that there were two types of static electricity, which also repel or attract each other like magnets. Yet he did not realize the connection between static electricity and magnetism. More than a hundred years passed, and in the light of Newton's success in formulating the laws of gravity and its uses, scientists tried to find a quantitative expression for magnetic forces. The French physicist Charles-Augustin de Coulomb (1726–1806), after whom the unit of electrical charge (coulomb) is named, discovered that the power of attraction between two magnets and the repulsive force of electrical charges act in a similar fashion to the force of gravity; in other words, the force is proportional to the size of the charge and reduces in proportion to the square of the distance. The mathematical expression was of a familiar form, and hence the law was accepted relatively easily. Moreover, an understanding started crystallizing that perhaps something of deeper significance was taking place, and that was the uniformity of the mathematical forms that describe nature. Further progress in understanding the essence of electricity was made by the Italian physicist Luigi Galvani (1737–1798), who showed that static electricity can cause a mechanical action. Among other things, he connected static electricity to frogs’ legs and found that it made the legs jump. This effect was given the name
galvanism
,
and still today students carry out those experiments in school. The Italian count Alessandro Volta (1745–1827), whose name is used for the unit of electric potential (the volt), showed that if one connects material with static electricity to material without static electricity by means of a metal bar, an electrical current is generated. He also showed how chemical processes can create static electricity and used that to build a primitive electric battery, the principle of which is used still today in the battery industry.

Until the beginning of the nineteenth century nothing was known of a physical connection between electricity and magnetism. The first such connection was brought to light in 1819 by the Danish physicist Hans Oersted (1777–1851). His discovery, apparently serendipitous, was that the needle of a compass changes direction when in the vicinity of an electric current. In other words, the current emits a force around it that affects the magnet. In about 1831, Joseph Henry (1797–1878) in the United States and Michael Faraday (1791–1867), one of England's leading physicists, discovered the second side of the connection between electricity and magnetism. They showed (independently of each other) that when a metal wire is passed close to a magnet, an electric current is produced in the metal. As an aside, we should add that Faraday, who devoted much effort to making science accessible to the public, was famous enough to merit a visit to his laboratory by King William IV. The king saw the experiment and asked, “Professor Faraday, of what use can this discovery be?” Faraday answered, “I don't know, but you will certainly be able collect a lot of tax on the results of this research.”