Mathematics and the Real World (23 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

The same problem of lack of intuition explaining a remote effect apparently exists with regard to gravity and Newton's laws. The important word here is
apparently
. The existence of the ether, that unseen, intangible medium that can transfer a force, explained the working of gravity. It was only in the wake of Maxwell's revolution that it became accepted that gravity also acts without a material medium. The predictions provided by Newton's equations, for example about the existence of the planet Neptune, were predictions about bodies of a known type with a firmly established intuition about their movement in nature. Maxwell's equations described physical phenomena using only mathematics. Maxwell in effect changed the way in which the world is described by mathematics. He forwent the physical explanation based on known physical quantities. He published his equations, as if declaring this is physics, the physics is inherent in mathematics. Although we cannot see or perceive the elements appearing in the mathematical equations in any other way, they are there, in nature. We can measure the effects of these elements on other bodies, measure the electricity they generate, utilize the force they exert, and so on, without being able to relate directly to their physical entity.
This conceptual revolution was not welcomed with open arms. Michael Faraday, then one of Britain's most eminent physicists, wrote to Maxwell in relatively blunt language (in this author's words, not verbatim): Would the mathematicians kindly translate the mathematical hieroglyphics in which their conclusions are written into comprehensible intuitive language so that the physicists might understand? As far as we know, Maxwell did not respond. In any case, the answer would have been negative. Physics is inherent in the mathematics that describes it.
Beyond the revolution in the approach, the difficulty in adopting Maxwell's theory lay in the fact that at that time all the elements that could be measured and that substantiated the correctness of the equations could also be explained using the physical mathematical relations that were known and accepted. Although there was not one comprehensive equation incorporating all the phenomena, the overall equation that Maxwell proposed
had no physical basis in terms of those days, and it predicted effects that no one had seen previously. It took twenty-five years from the publication of Maxwell's work, and eight years after his death, until Heinrich Hertz (1857–1894), a German physicist from the University of Bonn, succeeded in 1887 in producing an electromagnetic wave in the laboratory. There is no need to detail the importance of this physical discovery. Soon afterward, Maxwell's claim that light is an electromagnetic wave with a frequency we can perceive, that is, see, was confirmed. Its uses include radio transmissions, television, cellular telephones, microwave ovens, x-rays, and many others, all based on electromagnetic waves.
We should note that although Maxwell presented his equations without reference to the ether, he did not claim that the ether did not exist. The existence of the ether was still “required,” for example as a medium for Newton's gravitational forces. Maxwell claimed only that one could relate to how electromagnetic waves propagated by means of the mathematical equation they satisfied, without explaining the essence of the waves.
Maxwell's contribution was comparable to that of the Greeks in adopting mathematics to describe nature, and to that of Newton, who had the courage to develop a new mathematics to do so. Maxwell effectively changed the paradigm of the mathematical description of nature. No longer would a quantitative formulation of entities that the senses perceive directly or via a medium be the only way to proceed. Rather, the mathematical handling of abstract quantities, whose existence is justified simply by the fact that they explain effects that we can measure, became fully acceptable. Maxwell's contribution also changed the definition of a physicist. Today, if in the course of a conversation or a lecture I refer to Maxwell as a mathematician, some of my colleagues correct me, claiming that he was a physicist. Yet Faraday, one of the greatest physicists living in the time of Maxwell, refers to him as a mathematician who ought to translate his claims into the language of physics. Instead of doing that, Maxwell altered the definition of physics. Heinrich Hertz said, “Maxwell's theory is Maxwell's equation,” a statement that gives the essence of modern physics. Physics is inherent in the mathematics that describes it.
26. DISCREPANCY BETWEEN MAXWELL'S THEORY AND NEWTON'S THEORY
Maxwell's equations were amazing in their predictions of the discoveries that came later and fitted the observations and measurements performed in relation to those discoveries. Likewise, Newton's original equations and other equations that were derived using the mathematical instruments that he developed fitted physical reality perfectly. Yet there was a discrepancy between their equations, a discrepancy that threw doubt on whether both described the same physical world. We will describe that discrepancy.
Newton's second law,
F
=
ma
, states that the acceleration
a
of an object is proportional to the force
F
exerted upon it. The law does not relate to the speed of the object while the force is being exerted on it, but to its acceleration, that is, the change in its speed. Neither does the law of gravity relate to the speed of the object. The gravitational force acting on a body does not vary if it is moving or stationary. This non-dependence on the speed of the object is a blessing to mathematicians and physicists, and of course to engineers, because when measuring a change in speed as a result of the application of a force, there is no difference whether it is measured in relation to the Earth or in relation to another system of coordinates, such as a moving train. Newton presumed that the world had an absolute system of coordinates that can be used to measure the speed of every moving object. Although we cannot accurately identify this system, we are fortunate that it is not of any importance, since the laws of motion do not change if the speeds are measured with reference to some speed that is constant relative to the absolute system. Such systems are called inertial systems. The laws of motion do not change if one moves from one inertial system to another.
This property is lacking in Maxwell's equations. A transition from one system of coordinates to another, even if the second is moving at a constant speed relative to the first, alters the equation. We did not state Maxwell's equation explicitly, but it is not necessary to know its details to understand why a move from one system to another changes it. Maxwell's equation describing electromagnetic waves makes use of the speed of the wave.
When the speed appears explicitly in the equation, a change in the coordinates according to which the speed is measured changes the equation. In other words, Maxwell's equations are inconsistent with the invariance with respect to the inertial system in which Newton's equations are formulated.
The state of physics at that time can be summarized as follows: Newton's equations, which relate to a geometry that is consistent with our senses and whose relation has been accepted for hundreds and even thousands of years, accurately described many physical aspects of motion, including the propagation of waves in an earthly medium such as air or water. The movement described by the equations fits our intuition regarding the movement of objects, intuition that was formed in the course of the development of the human species. Maxwell's equations, on the other hand, predicted the existence of waves without indicating the medium in which those waves move, and their formulation is inconsistent with the known and familiar geometry. Those equations, however, were also astonishingly effective in predicting the physical effects relevant to them.
How do we proceed from here? One possibility is not to try to reconcile the two approaches. No discrepancy has been found between the two sets of equations. They describe different physical effects, and nobody can guarantee that there is one mathematical theory that covers the different effects in physics. A second possibility is to try to change one of the systems of equations for another system whose structure is consistent with that of the second. Many attempts were indeed made to replace Maxwell's relatively new equations with others in order to remove the discrepancy; none succeeded. Then Einstein came along and proposed a surprising third solution: he changed the geometric depiction of the world, that is to say he suggested a description of the geometry of the world that differs from what we feel it is but that reconciles the two systems of equations. Einstein's contribution was a huge breakthrough. It too came about following findings in physics, which we will discuss in section 28, and research in mathematics over many years into the geometry of the world. The salient aspects of that mathematical research are described in the next section.
27. THE GEOMETRY OF THE WORLD
To describe Einstein's theory of relativity with the correct perspective we must go back more than two millennia. We will repeat what axioms meant to the Greeks. They were basic working assumptions from which, by using the power of logic, they could develop mathematics further. The axioms themselves were obvious facts, physical truths, or ideal mathematical truths that did not need to be explained or substantiated. The geometry of the space in which we live could of course be examined mathematically, and Euclid summarized the mathematics of geometry in his book
Elements
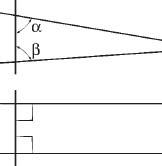
, where he presented the axioms of geometric space that had been formulated in classical Greece. Euclid formulated ten axioms and postulates (modern formulations show fourteen), including “self-evident” axioms such as, given two points, there is a straight line between them, and that a point in a plane and a given length from it define a circle with the point at its center and the given distance as its radius. Euclid formulated his fifth axiom, which in time became the parallel-lines postulate, as follows (see the upper part of the diagram below).
If a line transversing two lines forms on one side of it two angles whose sum is less than that of two right angles (i.e., less than 180 degrees), the extensions of the two lines will meet on that side
.
The formulation of the parallel-lines postulate accepted today states (see the lower part of the diagram):
Given a line and a point not on it, there is only one line that passes through that point that is parallel with the first line; parallel means that the extensions of the lines will never meet
.
Euclid himself made no reference to parallel lines, that is, straight lines that never meet. The reason was, apparently, the desire to avoid the assumption that there are lines that are infinite, having no end. As we wrote in section 7, Aristotle distinguished between infinity and potential infinity. He claimed that potential infinity existed so that, for example, we can draw lines as long as we want, but he denied the existence of infinity, that is, he denied that an infinite line exists. Euclid adopted that view in his books and avoided presenting and dealing with infinite quantities.
His fifth axiom caused unease even in Euclid's lifetime. The critics claimed that it was not obvious nor apparent from observing nature, and therefore it was not suitable to be included as an axiom. Attempts were made, therefore, to prove that property using other, self-evident axioms, but those attempts failed. Interest in this question continued for hundreds of years. Particularly noteworthy were the contribution and discussions of Omar Khayyám (1048–1131) and his school in Persia. It was there that Euclid's original fifth axiom was replaced by the parallel-lines postulate, which is accepted still today. There too it was proven that if one assumes the existence of infinite lines, the two versions are the same.
An interesting development that illustrates the complexity of the connection between mathematics and nature was made by the Italian mathematician Geraolamo Saccheri (1667–1733) of the University of Pavia. We will give the details of the case to show the difficulties that logical arguments are likely to cause. Saccheri used proof by contradiction, that is, he chose to assume that the parallel-lines axiom was not correct and tried to obtain a contradiction between that assumption and the other statements
that could be proven using the other axioms. In that way he would show that there was a contradiction deriving from the assumption that the axiom was incorrect so that the parallel-lines axiom is derived from the other axioms. We have shown previously that proof via reduction ad absurdum, or by contradiction, is not natural, and indeed it is difficult even to follow the steps that guided Saccheri, as we now show.
The parallel-lines axiom can be divided into two claims. The first is that there is a line parallel with the first line, and the second is that there is not more than one parallel line that passes through a given point not on that line. Saccheri first assumed that there is not even one parallel line that goes through the point, and he succeeded in finding a contradiction between that assumption (of no parallel line) and results that can be obtained from the other axioms. He concluded that there was at least one line parallel with the original line that went through the point not on the original line. He then assumed that there were two or more parallel lines that passed through the point. By means of a construction based on those two parallel lines he found such planes, however, with very strange properties, so much so that it was clear that they did not exist in the physical space we see around us. That was enough to convince Saccheri, and he declared that he had found the contradiction he was looking for and that the parallel-lines axiom is derived from the other axioms (because if we assume it is incorrect and we find a contradiction, then it is correct).