Statistics Essentials For Dummies (36 page)

Suppose you select a random sample of 50 paper towels from each brand and measure the absorbency of each paper towel. Suppose the average absorbency of Stats-absorbent (
x
) is 3 ounces, with a standard deviation of 0.9 ounces, and for Sponge-o-matic (
y
), the average absorbency is 3.5 ounces, with a standard deviation of 1.2 ounces.

Given these data, you have
= 3,
s
_x
= 0.9,
= 3.5,
s
_y
= 1.2, n1 = 50, and
n
₂
= 50. The difference between the sample means for (Stats-absorbent - Sponge-o-matic) is (3 - 3.5) = -0.5 ounces. (A negative difference simply means that the second sample mean was larger than the first.) The standard error is

. Divide the difference, -0.5,

by the standard error, 0.2121, which gives you -2.36. This is your test statistic.

To find the
p
-value, look up -2.36 on the
Z
-table (Table A-1 in the appendix). The chance of being beyond, in this case to the left of, -2.36 is equal to the percentile, which is 0.91%. Because H
_a
is a not-equal-to alternative, you double this percentage to get 2
×
0.91% = 1.82%. Change this to a probability by dividing by 100 to get a
p
-value of 0.0182 . This
p
-value is less than 0.05. That means you do have enough evidence to reject H
_o
.

Your conclusion is that a statistically significant difference exists between the absorbency levels of these two brands of paper towels, based on your samples. Sponge-o-matic comes out on top because it has a higher average.

If either of the sample sizes is small (generally less than 30), you use the
t
-distribution with
n
₁
+
n
₂
- 2 degrees of freedom (see Chapter 9) instead of the standard normal distribution when figuring out the
p
-value.

Testing the Mean Difference: Paired Data

This test is used when the variable is numerical (for example, cholesterol level or miles per gallon), and the individuals in the sample are either paired up in some way (identical twins are often used) or the same people are used twice (for example, using a pre-test and post-test). Paired tests are used for comparisons where you want to minimize the chance of the treatment and control groups being too different (and hence biased). See Chapter 13 for details.

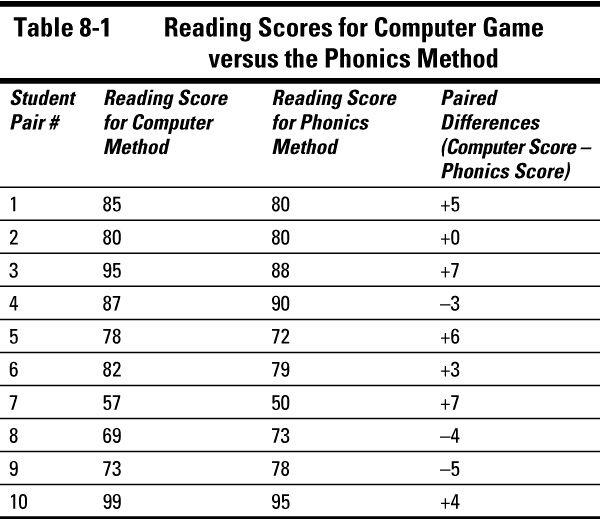
Suppose a researcher wants to see whether teaching students to read using a computer game gives better results than teaching with a tried-and-true phonics method. She randomly selects 20 students and puts them into 10 pairs according to their reading readiness level, age, IQ, and so on. She randomly selects one student from each pair to learn to read via the computer game, and the other learns to read using the phonics method. At the end of the study, each student takes the same reading test. The data are shown in Table 8-1.

The data are in pairs, but you're really interested only in the difference in reading scores (computer reading score - phonics reading score) for each pair, not the reading scores themselves. So, you take the difference between the scores for each pair, and those
paired differences
make up your new set of data to work with. If the two reading methods are the same, the average of the paired differences should be 0. If the computer method is better, the average of the paired differences should be positive (because the computer reading score should be larger than the phonics score).

Testing paired data amounts to testing one population mean, where the null hypothesis is that the mean (of the paired differences) is 0, and the alternative hypothesis is that the mean (of the paired differences) is > 0; < 0, or ≠ 0. The notation for the null hypothesis is H
_o
:
μ
_d
= 0, where
μ
_d
is the population mean of all paired differences. (The
d
in the subscript reminds you that you're working with the paired differences.)

The formula for the test statistic for paired differences is

. To calculate it, do the following:

1. For each pair of data, take the first value in the pair minus the second value in the pair to find the paired difference.

Think of the differences as your new data set.

2. Calculate the mean,
, and the standard deviation,
s
_d
, of all the differences in the pairs in the sample.

Let
n
represent the number of paired differences that you have.

3. Calculate the standard error:
.