Statistics Essentials For Dummies (37 page)

4. Take
divided by the standard error from Step 3.
Remember that
μ
d
= 0 if H
o
is true, so it's not included in the formula here.
For the reading scores example, you can use these steps to see whether the computer method is better at teaching students to read. Calculate the differences for each pair; you can see those differences in column 4 of Table 8-1. Notice that the sign on each of the differences is important; it indicates which method performed better for that particular pair.
The mean and standard deviation of the differences (column 4 of Table 8-1) must be calculated. The mean of the differences is found to be +2, and the standard deviation is 4.64. Note that
n
= 10 here. The standard error is 4.64 divided by the square root of 10 (which is 3.16). So you have 4.64/3.16 = 1.47. (Remember that
n
is the number of pairs, which is 10.) For the last step, take the mean of the differences, +2, divided by the standard error, which is 1.47, to get +1.36, the test statistic. That means the average difference for this sample is 1.36 standard errors above 0. Is this enough to say that a difference in reading scores applies to the whole population?
Because
n
is less than 30, you look up 1.36 on the
t
-distribution with 10 - 1 = 9 degrees of freedom (see Table A-2 in the appendix) to calculate the
p
-value (see Chapter 9). The
p
-value in this case is greater than 0.05 because 1.36 is close to the value of 1.38 on the table, and, therefore its
p
-value would be about 0.10 (the corresponding
p
-value for 1.38). That's because 1.38 is in the column under the 90th percentile, and because H
a
is a greater-than alternative, you take 100% - 90% = 10% = 0.10. Since the
p
-value is clearly greater than 0.05, you conclude that there isn't enough evidence to reject H
o
, so the computer game can't be touted as a better reading method. (This could be due to the lack of additional evidence needed to prove this with a smaller sample size.)
In many paired experiments, the data sets will be small due to costs and time associated with doing these kinds of studies. That means the
t
-distribution with
n
- 1 degrees of freedom (see Chapter 9) is often used instead of the standard normal distribution (see Table A-1 in the appendix) when figuring out the
p
-value.
Testing Two Population Proportions
This test is used when the variable is categorical (for example, smoker/nonsmoker, political party, support/oppose an opinion, and so on) and you're interested in the proportion of individuals with a certain characteristic — for example, the proportion of smokers. In this case, two populations or groups are being compared (such as the proportion of female smokers versus male smokers).
In order to conduct this test, two separate random samples need to be selected, one from each population. The null hypothesis is that the two population proportions are the same; in other words, that their difference is equal to 0. The notation for the null hypothesis is H
o
:
p
1
-
p
2
= 0, where
p
1
is the proportion from the first population, and
p
2
is the proportion from the second population.
Here is the formula for the test statistic comparing two proportions:
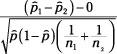
where
is the
pooled sample proportion,
aka the proportion of all individuals from the combined samples that have the characteristic of interest. To calculate it, do the following:
1. Calculate the sample proportions
and
.
For each sample, let
n
1
and
n
2
represent the two sample sizes (they need not be equal).
2. Find the difference between the two sample proportions,
.
3. Calculate the pooled sample proportion,
, which is the total number of individuals from both samples who have the characteristic of interest (for example, the total number of smokers, male or female, in the sample), divided by the total number of individuals from both samples (
n
1
+
n
2
).