Structure and Interpretation of Computer Programs (53 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

(define (delete-queue! queue)
(cond ((empty-queue? queue)
(error "DELETE! called with an empty queue" queue))
(else
(set-front-ptr! queue (cdr (front-ptr queue)))
queue)))
Exercise 3.21.
Ben Bitdiddle decides to test the queue implementation described
above. He types in the procedures to the Lisp interpreter and
proceeds to try them out:
(define q1 (make-queue))
(insert-queue! q1 'a)
((a) a)
(insert-queue! q1 'b)
((a b) b)
(delete-queue! q1)
((b) b)
(delete-queue! q1)
(() b)
“It's all wrong!” he complains. “The interpreter's response shows
that the last item is inserted into the queue twice. And when I
delete both items, the second
b
is still there, so the queue
isn't empty, even though it's supposed to be.” Eva Lu Ator suggests
that Ben has misunderstood what is happening. “It's not that the
items are going into the queue twice,” she explains. “It's just
that the standard Lisp printer doesn't know how to make sense of the
queue representation. If you want to see the queue printed correctly,
you'll have to define your own print procedure for queues.” Explain
what Eva Lu is talking about. In particular, show why Ben's examples
produce the printed results that they do. Define a procedure
print-queue
that takes a queue as input and prints the sequence of
items in the queue.
Exercise 3.22.
Instead of representing a queue as a pair of pointers, we can build a
queue as a procedure with local state. The local state will consist
of pointers to the beginning and the end of an ordinary list. Thus,
the
make-queue
procedure will have the form
(define (make-queue)
(let ((front-ptr
...
)
(rear-ptr
...
))
<
definitions of internal procedures
>
(define (dispatch m)
...
)
dispatch))
Complete the definition of
make-queue
and provide
implementations of the queue operations using this representation.
Exercise 3.23.
A
deque
(“double-ended queue”) is a sequence in which items
can be inserted and deleted at either the front or the rear.
Operations on deques are the constructor
make-deque
, the predicate
empty-deque?
, selectors
front-deque
and
rear-deque
, and mutators
front-insert-deque!
,
rear-insert-deque!
,
front-delete-deque!
, and
rear-delete-deque!
. Show how to represent deques using pairs, and
give implementations of the operations.
23
All operations should be accomplished in θ(1) steps.
When we studied various ways of representing sets in chapter 2, we
mentioned in section
2.3.3
the task of
maintaining a table of records indexed by identifying keys. In the
implementation of data-directed programming in
section
2.4.3
, we made extensive use of
two-dimensional tables, in which information is stored and retrieved
using two keys. Here we see how to build tables as mutable list
structures.
We first consider a one-dimensional table, in which each value is
stored under a single key. We implement the table as a list of
records, each of which is implemented as a pair consisting of a key
and the associated value. The records are glued together to form a
list by pairs whose
car
s point to successive records. These
gluing pairs are called the
backbone
of the table. In order to
have a place that we can change when we add a new record to the table,
we build the table as a
headed list
. A headed list has a
special backbone pair at the beginning, which holds a dummy
“record” – in this case the arbitrarily chosen symbol
*table*
.
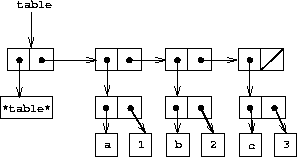
Figure
3.22
shows the box-and-pointer diagram for the table
a: 1
b: 2
c: 3
 |
To extract information from a table we use the
lookup
procedure, which takes a key as argument and returns the associated
value (or false if there is no value stored under that key).
Lookup
is defined in terms of the
assoc
operation, which
expects a key and a list of records as arguments. Note that
assoc
never sees the dummy record.
Assoc
returns the record
that has the given key as its
car
.
24
Lookup
then
checks to see that the resulting record returned by
assoc
is not
false, and returns the value (the
cdr
) of the record.
(define (lookup key table)
(let ((record (assoc key (cdr table))))
(if record
(cdr record)
false)))
(define (assoc key records)
(cond ((null? records) false)
((equal? key (caar records)) (car records))
(else (assoc key (cdr records)))))
To insert a value in a table under a specified key, we first use
assoc
to see if there is already a record in the table with this key.
If not, we form a new record by
cons
ing the key with the value,
and insert this at the head of the table's list of records, after the
dummy record. If there already is a record with this key, we set the
cdr
of this record to the designated new value. The header of
the table provides us with a fixed location to modify in order to
insert the new record.
25
(define (insert! key value table)
(let ((record (assoc key (cdr table))))
(if record
(set-cdr! record value)
(set-cdr! table
(cons (cons key value) (cdr table)))))
'ok)
To construct a new table, we simply create a list containing the
symbol
*table*
:
(define (make-table)
(list '*table*))
In a two-dimensional table, each value is indexed by two keys. We can
construct such a table as a one-dimensional table in which each key
identifies a subtable.
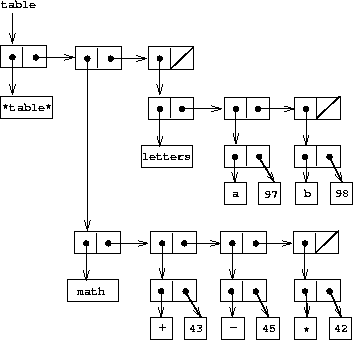
Figure
3.23
shows the box-and-pointer diagram for the table
math:
+: 43
-: 45
*: 42
letters:
a: 97
b: 98
which has two subtables. (The subtables don't need a
special header symbol, since the key that identifies the subtable
serves this purpose.)
 |
When we look up an item, we use the first key
to identify the correct subtable. Then we use the second key to
identify the record within the subtable.
(define (lookup key-1 key-2 table)
(let ((subtable (assoc key-1 (cdr table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(cdr record)
false))
false)))
To insert a new item under a pair of keys, we use
assoc
to see if
there is a subtable stored under the first key. If not, we build a
new subtable containing the single record (
key-2
,
value
)
and insert it into the table under the first key. If a subtable
already exists for the first key, we insert the new record into this
subtable, using the insertion method for one-dimensional tables
described above:
(define (insert! key-1 key-2 value table)
(let ((subtable (assoc key-1 (cdr table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(set-cdr! record value)
(set-cdr! subtable
(cons (cons key-2 value)
(cdr subtable)))))
(set-cdr! table
(cons (list key-1
(cons key-2 value))
(cdr table)))))
'ok)
The
lookup
and
insert!
operations defined above take the
table as an argument. This enables us to use programs that access
more than one table. Another way to deal with multiple tables is to
have separate
lookup
and
insert!
procedures for each
table. We can do this by representing a table procedurally, as an
object that maintains an internal table as part of its local state.
When sent an appropriate message, this “table object” supplies the
procedure with which to operate on the internal table. Here is a
generator for two-dimensional tables represented in this fashion:
(define (make-table)
(let ((local-table (list '*table*)))
(define (lookup key-1 key-2)
(let ((subtable (assoc key-1 (cdr local-table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(cdr record)
false))
false)))
(define (insert! key-1 key-2 value)
(let ((subtable (assoc key-1 (cdr local-table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(set-cdr! record value)
(set-cdr! subtable
(cons (cons key-2 value)
(cdr subtable)))))
(set-cdr! local-table
(cons (list key-1
(cons key-2 value))
(cdr local-table)))))
'ok)
(define (dispatch m)
(cond ((eq? m 'lookup-proc) lookup)
((eq? m 'insert-proc!) insert!)
(else (error "Unknown operation -- TABLE" m))))
dispatch))
Using
make-table
, we could implement the
get
and
put
operations used in section
2.4.3
for data-directed
programming, as follows:
(define operation-table (make-table))
(define get (operation-table 'lookup-proc))
(define put (operation-table 'insert-proc!))
Get
takes as arguments two keys, and
put
takes
as arguments two keys and a value. Both operations access the same
local table, which is encapsulated within the object created by the
call to
make-table
.
Exercise 3.24.
In the table implementations above, the keys are tested for equality
using
equal?
(called by
assoc
). This is not always the appropriate test. For
instance, we might have a table with numeric keys in which we don't
need an exact match to the number we're looking up,
but only a number within some tolerance of it.
Design a table constructor
make-table
that takes as an argument a
same-key?
procedure
that will be used to test “equality” of keys.
Make-table
should
return a
dispatch
procedure that can be used to access
appropriate
lookup
and
insert!
procedures for a local
table.
Exercise 3.25.
Generalizing one- and two-dimensional tables, show how to implement a
table in which values are stored under an arbitrary number of keys and
different values may be stored under different numbers of keys. The
lookup
and
insert!
procedures should take as input a list
of keys used to access the table.
Exercise 3.26.
To search a table as implemented above, one needs to scan through the
list of records. This is basically the unordered list representation of
section
2.3.3
. For large tables, it may be more
efficient to structure the table in a different manner. Describe a
table implementation where the (key, value) records are organized
using a binary tree, assuming that keys can be ordered in some way
(e.g., numerically or alphabetically). (Compare
exercise
2.66
of chapter 2.)