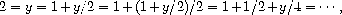Structure and Interpretation of Computer Programs (89 page)

(define (type exp)
  (if (pair? exp)
      (car exp)
      (error "Unknown expression TYPE" exp)))
(define (contents exp)
  (if (pair? exp)
      (cdr exp)
      (error "Unknown expression CONTENTS" exp)))

The following procedures, used by
query-driver-loop
(in section
4.4.4.1
), specify
that rules and assertions are added to the data base by expressions of
the form
(assert! <
rule-or-assertion
>):

(define (assertion-to-be-added? exp)
  (eq? (type exp) 'assert!))
(define (add-assertion-body exp)
  (car (contents exp)))

Here are the syntax definitions for the
and
,
or
,
not
, and
lisp-value
special forms
(section 
4.4.4.2
):

(define (empty-conjunction? exps) (null? exps))
(define (first-conjunct exps) (car exps))
(define (rest-conjuncts exps) (cdr exps))
(define (empty-disjunction? exps) (null? exps))
(define (first-disjunct exps) (car exps))
(define (rest-disjuncts exps) (cdr exps))
(define (negated-query exps) (car exps))
(define (predicate exps) (car exps))
(define (args exps) (cdr exps))

The following three procedures define the syntax of rules:

(define (rule? statement)
  (tagged-list? statement 'rule))
(define (conclusion rule) (cadr rule))
(define (rule-body rule)
  (if (null? (cddr rule))
      '(always-true)
      (caddr rule)))

Query-driver-loop
(section 
4.4.4.1
)
calls
query-syntax-process
to
transform pattern variables in the expression, which have the form
?symbol
, into the internal format
(? symbol)
. That is to
say, a pattern such as
(job ?x ?y)
is actually represented
internally by the system as
(job (? x) (? y))
. This increases
the efficiency of query processing, since it means that the system can
check to see if an expression is a pattern variable by checking
whether the
car
of the expression is the symbol
?
, rather
than having to extract characters from the symbol. The syntax
transformation is accomplished by the following
procedure:
⁸¹

(define (query-syntax-process exp)
  (map-over-symbols expand-question-mark exp))
(define (map-over-symbols proc exp)
  (cond ((pair? exp)
         (cons (map-over-symbols proc (car exp))
               (map-over-symbols proc (cdr exp))))
        ((symbol? exp) (proc exp))
        (else exp)))
(define (expand-question-mark symbol)
  (let ((chars (symbol->string symbol)))
    (if (string=? (substring chars 0 1) "?")
        (list '?
              (string->symbol
               (substring chars 1 (string-length chars))))
        symbol)))

Once the variables are transformed in this way, the variables in a
pattern are lists starting with
?
,
and the constant symbols (which need to be recognized for
data-base indexing, section 
4.4.4.5
) are just the symbols.

(define (var? exp)
  (tagged-list? exp '?))
(define (constant-symbol? exp) (symbol? exp))

Unique variables are constructed during rule application
(in section
4.4.4.4
) by means of
the following procedures. The unique identifier for a rule
application is a number, which is incremented each time a rule is
applied.

(define rule-counter 0)
(define (new-rule-application-id)
  (set! rule-counter (+ 1 rule-counter))
  rule-counter)
(define (make-new-variable var rule-application-id)
  (cons '? (cons rule-application-id (cdr var))))

When
query-driver-loop
instantiates the query to print the
answer, it converts any unbound pattern variables back to the right
form for printing, using

(define (contract-question-mark variable)
  (string->symbol
   (string-append "?" 
     (if (number? (cadr variable))
         (string-append (symbol->string (caddr variable))
                        "-"
                        (number->string (cadr variable)))
         (symbol->string (cadr variable))))))

Frames are represented as lists of bindings, which are
variable-value pairs:

(define (make-binding variable value)
  (cons variable value))
(define (binding-variable binding)
  (car binding))
(define (binding-value binding)
  (cdr binding))
(define (binding-in-frame variable frame)
  (assoc variable frame))
(define (extend variable value frame)
  (cons (make-binding variable value) frame))

Exercise 4.71.
  Louis Reasoner wonders why the
simple-query
and
disjoin
procedures (section 
4.4.4.2
) are implemented using
explicit
delay
operations, rather than being defined as follows:

(define (simple-query query-pattern frame-stream)
  (stream-flatmap
   (lambda (frame)
     (stream-append (find-assertions query-pattern frame)
                    (apply-rules query-pattern frame)))
   frame-stream))
(define (disjoin disjuncts frame-stream)
  (if (empty-disjunction? disjuncts)
      the-empty-stream
      (interleave
       (qeval (first-disjunct disjuncts) frame-stream)
       (disjoin (rest-disjuncts disjuncts) frame-stream))))

Can you give examples of queries where these simpler definitions would
lead to undesirable behavior?

Exercise 4.72.
  Why do
disjoin
and
stream-flatmap
interleave the
streams rather than simply append them? Give examples that illustrate
why interleaving works better. (Hint: Why did we use
interleave
in
section 
3.5.3
?)

Exercise 4.73.
  Why does
flatten-stream
use
delay
explicitly?
What would be wrong with defining it as follows:

(define (flatten-stream stream)
  (if (stream-null? stream)
      the-empty-stream
      (interleave
       (stream-car stream)
       (flatten-stream (stream-cdr stream)))))

Exercise 4.74.
  
Alyssa P. Hacker proposes to use a simpler version of
stream-flatmap
in
negate
,
lisp-value
, and
find-assertions
.
She observes that the procedure that is mapped over the frame stream
in these cases always produces either the empty stream or a singleton
stream, so no interleaving is needed when combining these streams.

a. Fill in the missing expressions in Alyssa's program.

(define (simple-stream-flatmap proc s)
  (simple-flatten (stream-map proc s)))
(define (simple-flatten stream)
  (stream-map <
??
>
              (stream-filter <
??
> stream)))

b. Does the query system's behavior change if we change it in this way?

Exercise 4.75.
  
Implement for the query language a new special form called
unique
.
Unique
should succeed if there is precisely one item
in the data base satisfying a specified query. For example,

(unique (job ?x (computer wizard)))

should print the one-item stream

(unique (job (Bitdiddle Ben) (computer wizard)))

since Ben is the only computer wizard, and

(unique (job ?x (computer programmer)))

should print the empty stream, since there is more than one computer
programmer. Moreover,

(and (job ?x ?j) (unique (job ?anyone ?j)))

should list all the jobs that are filled by only one person, and the
people who fill them.

There are two parts to implementing
unique
. The first is to
write a procedure that handles this special form, and the second is to make
qeval
dispatch to that procedure. The second part is trivial,
since
qeval
does its dispatching in a data-directed way. If
your procedure is called
uniquely-asserted
, all you need to do
is

(put 'unique 'qeval uniquely-asserted)

and
qeval
will dispatch to this procedure for every query whose
type
(
car
) is the symbol
unique
.

The real problem is to write the procedure
uniquely-asserted
.
This should take as input the
contents
(
cdr
) of the
unique
query, together with a stream of frames. For each frame in
the stream, it should use
qeval
to find the stream of all
extensions to the frame that satisfy the given query. Any stream that
does not have exactly one item in it should be eliminated. The
remaining streams should be passed back to be accumulated into one big
stream that is the result of the
unique
query. This is similar
to the implementation of the
not
special form.

Test your implementation by forming a query that lists all people who
supervise precisely one person.

Exercise 4.76.
  
Our implementation of
and
as a series combination of queries
(figure 
4.5
) is elegant, but it is inefficient because in
processing the second query of the
and
we must scan the data
base for each frame produced by the first query. If the data base has
N
elements, and a typical query produces a number of output frames
proportional to
N
(say
N
/
k
), then scanning the data base for each
frame produced by the first query will require
N
²
/
k
calls to the
pattern matcher. Another approach would be to process the two clauses
of the
and
separately, then look for all pairs of output frames
that are compatible. If each query produces
N
/
k
output frames, then
this means that we must perform
N
²
/
k
²
compatibility checks – a
factor of
k
fewer than the number of matches required in our current
method.

Devise an implementation of
and
that uses this strategy. You
must implement a procedure that takes two frames as inputs, checks
whether the bindings in the frames are compatible, and, if so,
produces a frame that merges the two sets of bindings. This operation
is similar to unification.

Exercise 4.77.
  
In section 
4.4.3
we saw that
not
and
lisp-value
can cause the query language to give “wrong” answers if
these filtering operations are applied to frames in which variables
are unbound. Devise a way to fix this shortcoming. One idea is to
perform the filtering in a “delayed” manner by appending to the
frame a “promise” to filter that is fulfilled only when enough
variables have been bound to make the operation possible. We could
wait to perform filtering until all other operations have been
performed. However, for efficiency's sake, we would like to perform
filtering as soon as possible so as to cut down on the number of
intermediate frames generated.

Exercise 4.78.
  
Redesign the query language as a nondeterministic program to be
implemented using the evaluator of
section 
4.3
, rather than as a stream
process. In this approach, each query will produce a single answer
(rather than the stream of all answers) and the user can type
try-again
to see more answers. You should find that much of the
mechanism we built in this section is subsumed by nondeterministic
search and backtracking. You will probably also find, however, that
your new query language has subtle differences in behavior from the
one implemented here. Can you find examples that illustrate this
difference?

Exercise 4.79.
  
When we implemented the Lisp evaluator in section 
4.1
,
we saw how to use local environments to avoid name conflicts between
the parameters of procedures. For example, in evaluating

(define (square x)
  (* x x))
(define (sum-of-squares x y)
  (+ (square x) (square y)))
(sum-of-squares 3 4)

there is no confusion between the
x
in
square
and the
x
in
sum-of-squares
, because we evaluate the body of each
procedure in an environment that is specially constructed to contain
bindings for the local variables. In the query system, we used a
different strategy to avoid name conflicts in applying rules. Each
time we apply a rule we rename the variables with new names that are
guaranteed to be unique. The analogous strategy for the Lisp
evaluator would be to do away with local environments and simply
rename the variables in the body of a procedure each time we apply the
procedure.

Implement for the query language a rule-application method that uses
environments rather than renaming. See if you can build on your
environment structure to create constructs in the query language for
dealing with large systems, such as the rule analog of
block-structured procedures. Can you relate any of this to the
problem of making deductions in a context (e.g., “If I supposed that
P
were true, then I would be able to deduce
A
and
B
.”) as a
method of problem solving? (This problem is open-ended. A good
answer is probably worth a Ph.D.)

⁵⁸
Logic programming has grown out of a long
history of research in automatic theorem proving. Early
theorem-proving programs could accomplish very little, because they
exhaustively searched the space of possible proofs. The major
breakthrough that made such a search plausible was the discovery in
the early 1960s of the
unification algorithm
and the
resolution principle
(Robinson 1965). Resolution was used, for
example, by
Green and Raphael (1968) (see also Green 1969) as the
basis for a deductive question-answering system. During most of this
period, researchers concentrated on algorithms that are guaranteed to
find a proof if one exists. Such algorithms were difficult to control
and to direct toward a proof.
Hewitt (1969) recognized the
possibility of merging the control structure of a programming language
with the operations of a logic-manipulation system, leading to the
work in automatic search mentioned in section 
4.3.1
(footnote 
47
). At the same time that this was being done,
Colmerauer, in Marseille, was developing rule-based systems for
manipulating natural language (see Colmerauer et al. 1973). He
invented a programming language called
Prolog for representing those
rules.
Kowalski (1973; 1979), in Edinburgh, recognized that execution
of a Prolog program could be interpreted as proving theorems (using a
proof technique called linear
Horn-clause resolution). The merging of
the last two strands led to the logic-programming movement. Thus, in
assigning credit for the development of logic programming, the French
can point to Prolog's genesis at the
University of Marseille, while
the British can highlight the work at the
University of Edinburgh.
According to people at
MIT, logic programming was developed by these
groups in an attempt to figure out what Hewitt was talking about in
his brilliant but impenetrable Ph.D. thesis. For a history of logic
programming, see Robinson 1983.

⁵⁹
To
see the correspondence between the rules and the procedure, let
x
in the procedure (where
x
is nonempty) correspond to
(cons u v)
in the rule. Then
z
in the rule corresponds to the
append
of
(cdr x)
and
y
.

⁶⁰
This certainly does not
relieve the user of the entire problem of how to compute the answer.
There are many different mathematically equivalent sets of rules for
formulating the
append
relation, only some of which can be
turned into effective devices for computing in any direction. In
addition, sometimes “what is” information gives no clue “how to”
compute an answer. For example, consider the problem of computing the
y
such that
y
²
=
x
.

⁶¹
Interest in logic programming peaked
during the early 80s when the Japanese government began an ambitious
project aimed at building superfast computers optimized to run logic
programming languages. The speed of such computers was to be measured
in LIPS (Logical Inferences Per Second) rather than the usual FLOPS
(FLoating-point Operations Per Second). Although the project
succeeded in developing hardware and software as originally planned,
the international computer industry moved in a different direction.
See
Feigenbaum and Shrobe 1993 for an overview evaluation of the
Japanese project. The logic programming community has also moved on
to consider relational programming based on techniques other than
simple pattern matching, such as the ability to deal with numerical
constraints such as the ones illustrated in the constraint-propagation
system of section 
3.3.5
.

⁶²
This uses the dotted-tail notation introduced in
exercise 
2.20
.

⁶³
Actually, this description of
not
is valid only for simple cases. The real behavior of
not
is more complex. We will examine
not
's peculiarities in
sections 
4.4.2
and 
4.4.3
.

⁶⁴
Lisp-value
should be used only to perform an operation not
provided in the query language. In particular, it should not
be used to test equality (since that is what the matching in the
query language is designed to do) or inequality (since that can
be done with the
same
rule shown below).

⁶⁵
Notice that we do not need
same
in order to make two things be
the same: We just use the same pattern variable for each – in effect,
we have one thing instead of two things in the first place. For
example, see
?town
in the
lives-near
rule and
?middle-manager
in the
wheel
rule below.
Same
is useful when we want to force two things to be
different, such as
?person-1
and
?person-2
in the
lives-near
rule. Although using the same pattern variable in two
parts of a query forces the same value to appear in both places, using
different pattern variables does not force different values to appear.
(The values assigned to different pattern variables may be the same or
different.)

⁶⁶
We will also allow rules without bodies, as in
same
, and we will interpret such a rule to mean that the rule
conclusion is satisfied by any values of the variables.

⁶⁷
Because matching is generally very expensive, we would
like to avoid applying the full matcher to every element of the data
base. This is usually arranged by breaking up the process into a
fast, coarse match and the final match. The coarse match filters the
data base to produce a small set of candidates for the final match.
With care, we can arrange our data base so that some of the work of
coarse matching can be done when the data base is constructed rather
then when we want to select the candidates. This is called
indexing
the data base. There is a vast technology built around
data-base-indexing schemes. Our implementation, described in
section 
4.4.4
, contains a
simple-minded form of such an optimization.

⁶⁸
But this kind of exponential explosion is not common in
and
queries because the added conditions tend to reduce rather than expand
the number of frames produced.

⁶⁹
There is a large literature on data-base-management
systems that is concerned with how to handle complex queries
efficiently.

⁷⁰
There is a subtle difference between this filter
implementation of
not
and the usual meaning of
not
in
mathematical logic. See section 
4.4.3
.

⁷¹
In one-sided pattern matching, all the equations that
contain pattern variables are explicit and already solved for the
unknown (the pattern variable).

⁷²
Another way to think of unification is that it generates the most
general pattern that is a specialization of the two input patterns.
That is, the unification of
(?x a)
and
((b ?y) ?z)
is
((b ?y) a)
, and the unification of
(?x a ?y)
and
(?y ?z
a)
, discussed above, is
(a a a)
.
For our implementation, it is more convenient to think of the result
of unification as a frame rather than a pattern.

⁷³
Since unification is a
generalization of matching, we could simplify the system by using the
unifier to produce both streams. Treating the easy case with the
simple matcher, however, illustrates how matching (as opposed to
full-blown unification) can be useful in its own right.

⁷⁴
The reason we use streams (rather than lists) of frames is that the
recursive application of rules can generate
infinite numbers of values that satisfy a query. The delayed
evaluation embodied in streams is crucial here: The system will print
responses one by one as they are generated, regardless of whether
there are a finite or infinite number of responses.

⁷⁵
That a particular method of inference is
legitimate is not a trivial assertion. One must prove that if one
starts with true premises, only true conclusions can be derived. The
method of inference represented by rule applications is
modus
ponens
, the familiar method of inference that says that if
A
is
true and
A implies B
is true, then we may conclude that
B
is true.

⁷⁶
We must qualify this statement by
agreeing that, in speaking of the “inference” accomplished by a
logic program, we assume that the computation terminates.
Unfortunately, even this qualified statement is false for our
implementation of the query language (and also false for programs in
Prolog and most other current logic programming languages) because of
our use of
not
and
lisp-value
. As we will describe below,
the
not
implemented in the query language is not always
consistent with the
not
of mathematical logic, and
lisp-value
introduces additional complications. We could implement a
language consistent with mathematical logic by simply removing
not
and
lisp-value
from the language and agreeing to write
programs using only simple queries,
and
, and
or
. However,
this would greatly restrict the expressive power of the language. One
of the major concerns of research in logic programming is to find ways
to achieve more consistency with mathematical logic without unduly
sacrificing expressive power.

⁷⁷
This is not a problem of the logic but one of the
procedural interpretation of the logic provided by our interpreter.
We could write an interpreter that would not fall into a loop here.
For example, we could enumerate all the proofs derivable from our
assertions and our rules in a breadth-first rather than a depth-first
order. However, such a system makes it more difficult to take
advantage of the order of deductions in our programs. One attempt to
build sophisticated control into such a program is described in
deKleer et al. 1977. Another technique, which does not lead to such
serious control problems, is to put in special knowledge, such as
detectors for particular kinds of loops
(exercise 
4.67
). However, there can be no
general scheme for reliably preventing a system from going down
infinite paths in performing deductions. Imagine a diabolical rule of
the form “To show
P
(
x
) is true, show that
P
(
f
(
x
)) is true,” for
some suitably chosen function
f
.

⁷⁸
Consider the query
(not (baseball-fan (Bitdiddle Ben)))
. The system finds that
(baseball-fan (Bitdiddle Ben))
is not in the data base, so the empty
frame does not satisfy the pattern and is not filtered out of the
initial stream of frames. The result of the query is thus the empty
frame, which is used to instantiate the input query to produce
(not (baseball-fan (Bitdiddle Ben)))
.

⁷⁹
A discussion and justification of this
treatment of
not
can be found in the article by Clark (1978).

⁸⁰
In general, unifying
?y
with an expression involving
?y
would require our being able to find a fixed point of the
equation
?y
= <
expression involving
?y
>. It is
sometimes possible to syntactically form an expression that appears to
be the solution. For example,
?y
  =  
(f ?y)
seems to have
the fixed point
(f (f (f
...
)))
, which we can produce by
beginning with the expression
(f ?y)
and repeatedly substituting
(f ?y)
for
?y
. Unfortunately, not every such equation has
a meaningful fixed point. The issues that arise here are similar to
the issues of manipulating
infinite series in mathematics. For
example, we know that 2 is the solution to the equation
y
= 1 +
y
/2.
Beginning with the expression 1 +
y
/2 and repeatedly substituting 1
+
y
/2 for
y
gives