Structure and Interpretation of Computer Programs (92 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

Consider the GCD machine. The machine has an instruction that computes
the remainder of the contents of registers
a
and
b
and
assigns the result to register
t
. If we want to construct the
GCD machine without using a primitive remainder operation,
we must specify how to compute remainders in terms of simpler
operations, such as subtraction. Indeed, we can write a Scheme
procedure that finds remainders in this way:
(define (remainder n d)
(if (< n d)
n
(remainder (- n d) d)))
We can thus replace the remainder operation in the GCD machine's
data paths with a subtraction operation and a comparison test.
Figure
5.5
shows the data paths and controller
for the elaborated machine.
The instruction
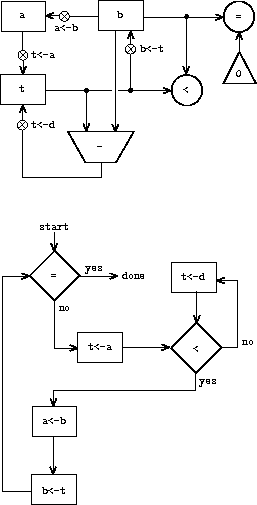 |
(assign t (op rem) (reg a) (reg b))
in the GCD controller definition is replaced by a sequence of
instructions that contains a loop, as shown in
figure
5.6
.
(controller |
Exercise 5.3.
Design a machine to compute square roots using Newton's method, as
described in section
1.1.7
:
(define (sqrt x)
(define (good-enough? guess)
(< (abs (- (square guess) x)) 0.001))
(define (improve guess)
(average guess (/ x guess)))
(define (sqrt-iter guess)
(if (good-enough? guess)
guess
(sqrt-iter (improve guess))))
(sqrt-iter 1.0))
Begin by assuming that
good-enough?
and
improve
operations
are available as primitives. Then show how to expand these in terms
of arithmetic operations. Describe each version of the
sqrt
machine design by drawing a data-path diagram and writing a controller
definition in the register-machine language.
When designing a machine to perform a computation, we would often
prefer to arrange for components to be shared by different parts of
the computation rather than duplicate the components. Consider a
machine that includes two GCD computations – one that finds the GCD of
the contents of registers
a
and
b
and one that finds the
GCD of the contents of registers
c
and
d
. We might start
by assuming we have a primitive
gcd
operation, then expand the
two instances of
gcd
in terms of more primitive operations.
Figure
5.7
shows just the GCD portions of the
resulting machine's data paths, without showing how they connect to
the rest of the machine. The figure also shows the corresponding
portions of the machine's controller sequence.
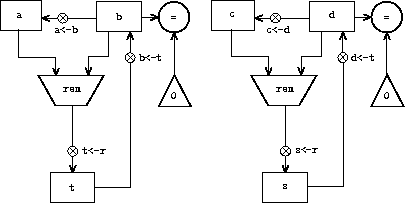 gcd-1 |
This machine has two remainder operation boxes and two boxes for
testing equality. If the duplicated components are complicated, as is the
remainder box, this will not be an economical way to build the
machine. We can avoid duplicating the data-path components by using
the same components for both GCD computations, provided that doing so
will not affect the rest of the larger machine's computation. If the
values in registers
a
and
b
are not needed by the time the
controller gets to
gcd-2
(or if these values can be moved to
other registers for safekeeping), we can change the machine so that
it uses registers
a
and
b
, rather than registers
c
and
d
, in computing the second GCD as well as the first. If we
do this, we obtain the controller sequence shown in
figure
5.8
.
We have removed the duplicate data-path components
(so that the data paths are again as in figure
5.1
),
but the controller
now has two GCD sequences that differ only in their entry-point
labels. It would be better to replace these two sequences by branches
to a single sequence – a
gcd
subroutine
– at the end of
which we branch back to the correct place in the main instruction
sequence. We can accomplish this as follows: Before branching to
gcd
, we place a distinguishing value (such as 0 or 1) into a special
register,
continue
. At the end of the
gcd
subroutine we
return either to
after-gcd-1
or to
after-gcd-2
, depending
on the value of the
continue
register.
Figure
5.9
shows the relevant portion of the
resulting controller sequence, which includes only a single copy of the
gcd
instructions.
gcd-1 |
gcd |
gcd |
This is a reasonable approach for handling small problems, but it
would be awkward if there were many instances of GCD computations in
the controller sequence. To decide where to continue executing after
the
gcd
subroutine, we would need tests in the data paths and
branch instructions in the controller for all the places that use
gcd
. A more powerful method for implementing subroutines is to have
the
continue
register hold the label of the entry point in the
controller sequence at which execution should continue when the
subroutine is finished. Implementing this strategy requires a new
kind of connection between the data paths and the controller of a
register machine: There must be a way to assign to a register a label
in the controller sequence in such a way that this value can be fetched
from the register and used to continue execution at the designated
entry point.
To reflect this ability, we will extend the
assign
instruction of the register-machine language to allow a register to be
assigned as value a label from the controller sequence (as a special
kind of constant). We will also extend the
goto
instruction to
allow execution to continue at the entry point described by the
contents of a register rather than only at an entry point described by
a constant label. Using these new constructs we can terminate the
gcd
subroutine with a branch to the location stored in the
continue
register. This leads to the controller sequence shown in
figure
5.10
.
A machine with more than one subroutine could use multiple
continuation registers (e.g.,
gcd-continue
,
factorial-continue
) or we could have all subroutines share a single
continue
register. Sharing is more economical, but we must be
careful if we have a subroutine (
sub1
) that calls another
subroutine (
sub2
). Unless
sub1
saves the contents of
continue
in some other register before setting up
continue
for
the call to
sub2
,
sub1
will not know where to go when it
is finished. The mechanism developed in the next section to handle
recursion also provides a better solution to this problem of nested
subroutine calls.
With the ideas illustrated so far, we can implement any iterative
process by specifying a register machine that has a register
corresponding to each state variable of the process. The machine
repeatedly executes a controller loop, changing the contents
of the registers, until some termination condition is satisfied. At
each point in the controller sequence, the state of the machine
(representing the state of the iterative process) is completely
determined by the contents of the registers (the values of the state
variables).
Implementing recursive processes, however, requires an additional
mechanism. Consider the following recursive method for computing
factorials, which we first examined in
section
1.2.1
:
(define (factorial n)
(if (= n 1)
1
(* (factorial (- n 1)) n)))
As we see from the procedure, computing
n
! requires computing
(
n
- 1)!. Our GCD machine, modeled on the procedure
(define (gcd a b)
(if (= b 0)
a
(gcd b (remainder a b))))
similarly had to compute another GCD. But there is an important
difference between the
gcd
procedure, which reduces the original
computation to a new GCD computation, and
factorial
, which
requires computing another factorial as a subproblem. In GCD, the
answer to the new GCD computation is the answer to the original
problem. To compute the next GCD, we simply place the new arguments
in the input registers of the GCD machine and reuse the
machine's data paths by executing the same controller sequence. When
the machine is finished solving the final GCD problem, it has
completed the entire computation.