The Ascent of Man (15 page)

Mathematics is in many ways the most elaborated and sophisticated of the sciences – or so it seems to me, as a mathematician. So I find both a special pleasure and constraint in describing the progress of mathematics, because it has been part of so much human speculation: a ladder for mystical as well as rational thought in the intellectual ascent of man.
However, there are some concepts that any account of mathematics should include: the logical idea of proof, the empirical idea of exact laws of nature (of space particularly), the emergence of the concept of operations, and the movement in mathematics from a static to a dynamic description of nature. They form the theme of this essay.

Even very primitive peoples have a number system; they may
not count much beyond four, but they know that two of any thing plus two of the same thing makes four, not just sometimes but always. From that fundamental step, many cultures have built their own number systems, usually as a written language with similar conventions. The Babylonians, the Mayans, and the people of India, for example, invented essentially the same way of writing large numbers as a
sequence of digits that we use, although they lived far apart in space and in time.

So there is no place and no moment in history where I could stand and say ‘Arithmetic begins here, now’. People have been counting, as they have been talking, in every culture. Arithmetic, like language, begins in legend. But mathematics in our sense, reasoning with numbers, is another matter. And it is to look
for the origin of that, at the hinge of legend and history, that I went sailing to the island of Samos.

In legendary times Samos was a centre of the Greek worship of Hera, the Queen of Heaven, the lawful (and jealous) wife of Zeus. What remains of her temple, the Heraion, dates from the sixth century before Christ. At that time there was born on Samos, about 580
BC
, the first genius and the founder
of Greek mathematics, Pythagoras. During his lifetime the island was taken over by the tyrant, Polycrates. There is a tradition that before Pythagoras fled, he taught for a while in hiding in a small white cave in the mountains which is still shown to the credulous.

Samos is a magical island. The air is full of sea and trees and music. Other Greek islands will do as a setting for
The Tempest
, but for me this is Prospero’s island, the shore where the scholar turned magician. Perhaps Pythagoras was a kind of magician to his followers, because he taught them that nature is commanded by numbers. There is a harmony in nature, he said, a unity in her variety, and it has a language: numbers are the language of nature.

Pythagoras found a basic relation between musical harmony and mathematics.
The story of his discovery survives only in garbled form, like a folk tale. But what he discovered was precise. A single stretched string vibrating as a whole produces a ground note. The notes that sound harmonious with it are produced by dividing the string into an exact number of parts: into exactly two parts, into exactly three parts, into exactly four parts, and so on. If the still
point on
the string, the node, does not come at one of these exact points, the sound is discordant.

As we shift the node along the string, we recognise the notes that are harmonious when we reach the prescribed points. Begin with the whole string: this is the ground note. Move the node to the midpoint: this is the octave above it. Move the node to a point one third of the way along: this is the fifth above that. Move it to a point one fourth along: this is
the fourth, another octave above. And if you move the node to a point one fifth of the way along, this (which Pythagoras did not reach) is the major third above that.

Pythagoras had found that the chords which sound pleasing to the ear – the western ear – correspond to exact divisions of the string by whole numbers. To the Pythagoreans that discovery had a mystic force. The agreement between
nature and number was so cogent that it persuaded them that not only the sounds of nature, but all her characteristic dimensions, must be simple numbers that express harmonies. For example, Pythagoras or his followers believed that we should be able to calculate the orbits of the heavenly bodies (which the Greeks pictured as carried round the earth on crystal spheres) by relating them to the musical
intervals. They felt that all the regularities in nature are musical; the movements of the heavens were, for them, the music of the spheres.

These ideas gave Pythagoras the status of a seer in philosophy, almost a religious leader, whose followers formed a secret and perhaps revolutionary sect. It is likely that many of the later followers of Pythagoras were slaves; they believed in the transmigration
of souls, which may have been their way of hoping for a happier life after death.

I have been speaking of the language of numbers, that is arithmetic, but my last example was the heavenly spheres, which are geometrical shapes. The transition is not accidental. Nature presents us with shapes: a wave, a crystal, the human body, and it is we who have to sense and find the numerical relations in
them. Pythagoras was a pioneer in linking geometry with numbers, and since it is also my choice among the branches of mathematics, it is fitting to watch what he did.

Pythagoras had proved that the world of sound is governed by exact numbers. He went on to prove that the same thing is true of the world of vision. That is an extraordinary achievement. I look about me; here I am, in this marvellous,
coloured landscape of Greece, among the wild natural forms, the Orphic dells, the sea. Where under this beautiful chaos can there lie a simple, numerical structure?

The question forces us back to the most primitive constants in our perception of natural laws. To answer well, it is clear that we must begin from universals of experience. There are two experiences on which our visual world is based:
that gravity is vertical, and that the horizon stands at right angles to it. And it is that conjunction, those cross-wires in the visual field, which fixes the nature of the right angle; so that if I were to turn this right angle of experience (the direction of ‘down’ and the direction of sideways’) four times, back I come to the cross of gravity and the horizon. The right angle is defined by
this fourfold operation, and is distinguished by it from any other arbitrary angle.

In the world of vision, then, in the vertical picture plane that our eyes present to us, a right angle is defined by its fourfold rotation back on itself. The same definition holds also in the horizontal world of experience, in which
in fact we move. Consider that world, the world of the flat earth and the map
and the points of the compass. Here I am looking across the straits from Samos to Asia Minor, due south. I take a triangular tile as a pointer and I set it pointing there, south. (I have made the pointer in the shape of a right-angled triangle, because I shall want to put its four rotations side by side.) If I turn that triangular tile through a right angle, it points due west. If I now turn it through
a second right angle, it points due north. And if I now turn it through a third right angle, it points due east. Finally, the fourth and last turn will take it due south again, pointing to Asia Minor, in the direction in which it began.

Not only the natural world as we experience it, but the world as we construct it is built on that relation. It has been so since the time that the Babylonians
built the Hanging Gardens, and earlier, since the time that the Egyptians built the pyramids. These cultures already knew in a practical sense that there is a builder’s set square in which the numerical relations dictate and make the right angle. The Babylonians knew many, perhaps hundreds of formulae for this by 2000
BC
. The Indians and the Egyptians knew some. The Egyptians, it seems, almost
always used a set square with the sides of the triangle made of three, four, and five units. It was not until 550
BC
or thereabouts that Pythagoras raised this knowledge out of the world of empirical fact into the world of what we should now call proof. That is, he asked the question, ‘How do such numbers that make up these builder’s triangles flow from the fact that a right angle is what you
turn four times to point the same way?’

His proof, we think, ran something like this. (It is not the proof that stands in the school books.) The four leading points – south, west, north, east – of the triangles that form the cross of the compass are the corners of a square. I slide the four triangles so that the long side of each ends at the leading point of a neighbour. Now I have constructed
a square on the longest side of the right-angled triangles – on the hypotenuse. Just so that we should know what is part of the enclosed area and what is not, I will fill in the small inner square area that has now been uncovered with an additional tile. (I use tiles because many tile patterns, in Rome, in the Orient, from now on derive from this kind of wedding of mathematical relation to thought
about nature.)

Now we have a square on the hypotenuse, and we can of course relate that by calculation to the squares on the two shorter sides. But that would miss the natural structure and inwardness of the figure. We do not need any calculation. A small game, such as children and mathematicians play, will reveal more than calculation. Transpose two triangles to new positions, thus. Move the
triangle that pointed south so that its longest side lies along the longest side of the triangle that pointed north. And move the triangle that pointed east so that its longest side lies along the longest side of the triangle that pointed west.

Now we have constructed an L-shaped figure with the same area (of course, because it is made of the same pieces) whose sides we can see at once in terms
of the smaller sides of the right-angled triangle. Let me make the composition of the L-shaped figure visible: put a divider down that separates the end of the L from the upright part. Then it is clear that the end is a square on the shorter side of the triangle; and the upright part of the L is a square on the longer of the two sides enclosing the right angle.

Pythagoras had thus proved a general
theorem: not just for the 3 : 4 : 5 triangle of Egypt, or any Babylonian triangle, but for every triangle that contains a right angle. He had proved that the square on the longest side or hypotenuse is equal to the square on one of the
other two sides plus the square on the other if, and only if, the angle they contain is a right angle. For instance, the sides 3 : 4 : 5 compose a right-angled
triangle because

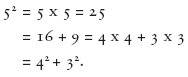
And the same is true of the sides of triangles found by the Babylonians, whether simple as 8 : 15 : 17, or forbidding as 3367 : 3456 : 4825, which leave no doubt that they were good at arithmetic.

To this day, the theorem of Pythagoras remains the most important single theorem in the whole of mathematics. That seems a bold and extraordinary thing to say, yet it is not extravagant; because what Pythagoras established is a fundamental characterisation of the space in which we move, and it is the first time that is translated into numbers. And the exact fit of the numbers describes the exact
laws that bind the universe. In fact, the numbers that compose right-angled triangles have been proposed as messages which we might send out to planets in other star systems as a test for the existence of rational life there.

The point is that the theorem of Pythagoras in the form in which I have proved it is an elucidation of the symmetry of plane space; the right angle is the element of symmetry
that divides the plane four ways. If plane space had a different kind of symmetry, the theorem would not be true; some other relation between the sides of special triangles would be true. And space is just as crucial a part of nature as matter is, even if (like the air) it is invisible; that is what the science of geometry is about. Symmetry is not merely a descriptive nicety; like other thoughts
in Pythagoras, it penetrates to the harmony in nature.

When Pythagoras had proved the great theorem, he offered a hundred oxen to the Muses in thanks for the inspiration. It is a gesture of pride and humility together, such as every scientist feels to this day when the numbers dovetail and say, ‘This is a part of, a key to, the structure of nature herself’.