The Ascent of Man (18 page)
Authors: Jacob Bronowski

In early perspective it was customary to use a sight and a grid to hold the instant of vision. The sighting device comes from astronomy, and the squared paper on which the picture was drawn is now the stand-by of mathematics. All the natural details
in which Dürer delights are expressions of the dynamic of time: the ox and the ass, the blush of youth on the cheek of the Virgin. The picture is
The Adoration of the Magi
. The three wise men from the east have found their star, and what it announces is the birth of time.
The chalice at the centre of Dürer’s painting was a test-piece in teaching perspective. For example, we have Uccello’s analysis
of the way the chalice looks; we can turn it on the computer as the perspective artist did. His eye worked like a turntable to follow and explore its shifting shape, the elongation of the circles into ellipses, and to catch the moment of time as a trace in space.
Analysing the changing movement of an object, as I can do on the computer, was quite foreign to Greek and to Islamic minds. They looked
always for what was unchanging and static, a timeless world of perfect order. The most perfect shape to them was the circle. Motion must run smoothly and uniformly in circles; that was the harmony of the spheres.
This is why the Ptolemaic system was built up of circles, along which time ran uniformly and imperturbably. But movements in the real world are not uniform. They change direction and
speed at every instant, and they cannot be analysed until a mathematics is invented in which time is a variable. That is a theoretical problem in the heavens, but it is practical and immediate on earth – in the flight of a projectile, in the spurting growth of a plant, in the single splash of a drop of liquid that goes through abrupt changes of shape and direction. The Renaissance did not have the
technical equipment to stop the picture frame instant by instant. But the Renaissance had the intellectual equipment: the inner eye of the painter, and the logic of the mathematician.
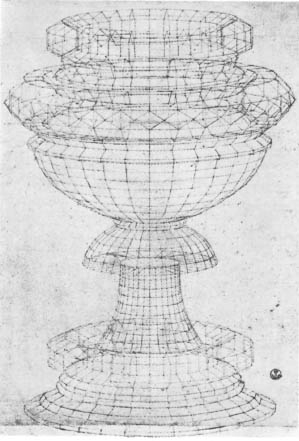 The moment of time as a trace in space.
The moment of time as a trace in space.Paolo Uccello’s perspective analysis of a chalice
.
In this way Johannes Kepler after the year 1600 became convinced that the motion of a planet is not circular and not uniform. It is an ellipse along which the planet runs at varying speeds. That means that the old mathematics of static patterns will no longer suffice, nor the mathematics of uniform motion.
You need a new mathematics to define and operate with instantaneous motion.
The mathematics of instantaneous motion was invented by two superb minds of the late seventeenth century – Isaac Newton and Gottfried Wilhelm Leibniz. It is now so familiar to us that we think of time as a natural element in a description of nature; but that was not always so. It was they who brought in the idea of a
tangent, the idea of acceleration, the idea of slope, the idea of infinitesimal, of differential. There is a word that has been forgotten but that is really the best name for that flux of time that Newton stopped like a shutter:
Fluxions
was Newton’s name for what is usually called (after Leibniz) the differential calculus. To think of it merely as a more advanced technique is to miss its real
content. In it, mathematics becomes a dynamic mode of thought, and that is a major mental step in the ascent of man. The technical concept that makes it work is, oddly enough, the concept of an infinitesimal step; and the intellectual break-through came in giving a rigorous meaning to that. But we may leave the technical concept to the professionals, and be content to call it the mathematics of change.
The laws of nature had always been made of numbers since Pythagoras said that was the language of nature. But now the language of nature had to include numbers which described time. The laws of nature become laws of motion, and nature herself becomes not a series of static frames but a moving process.
THE STARRY MESSENGER
The first science in the modern sense that grew in the Mediterranean civilisation was astronomy. It is natural to come to astronomy straight from mathematics; after all, astronomy was developed first, and became a model for all the other sciences, just because it could be turned into exact numbers. That is not an idiosyncrasy on my part.
What is an idiosyncrasy
is that I should choose to begin the drama of the first Mediterranean science in the New World.
The rudiments of astronomy exist in all cultures, and were evidently important in the concerns of early peoples all over the world. One reason for this is clear. Astronomy is the knowledge that guides us through the cycle of the seasons – for example, by the apparent movement of the sun. In this way
there can be fixed a time when men should plant, should harvest, move their herds and so on. Therefore all settled cultures have a calendar to guide their plans, and this was true in the New World as it was in the river-basins of Babylon and Egypt.
An example is the civilisation of the Mayans that flourished before
AD
1000 in the isthmus of America between the Atlantic and the Pacific Oceans.
It has a claim to be the highest of the American cultures: it had a written language, skill in engineering, and original arts. The Mayan temple complexes, with their steep pyramids, housed some astronomers, and we have portraits of a group of them on a large altar stone that has survived. The altar commemorates an ancient astronomical congress that met in the year
AD
776. Sixteen mathematicians
came here to the famous centre of Mayan science, the sacred city of Copan in Central America.
The Mayans had a system of arithmetic which was far ahead of Europe; for example, they had a symbol for zero. They were good mathematicians; nevertheless, they did not map the motions of the stars, except the simplest. Instead, their ritual was obsessed with the passage of time, and this formal concern
dominated their astronomy as it did their poems and legends.
When the great conference met at Copan, the Mayan priest astronomers had run into difficulty. We might suppose that such a major difficulty, calling for learned delegates to come from many centres, would turn on some real problem of observation. But we would be wrong. The congress was called to resolve an arithmetical problem of computation
that perpetually troubled the Mayan guardians of the calendar. They kept two calendars, one sacred and one profane, which were never in step for long; and they spent their ingenuity trying to stop the drift between them. The Mayan astronomers had only simple rules for the planetary motions in the heavens, and they had no concept of their machinery. Their idea of astronomy was purely formal,
a matter of keeping their calendars right. That was all that was done in
AD
776 when the delegates proudly posed for their portraits.
The point is that astronomy does not stop at the calendar. There is another use among early peoples which, however, was not universal. The movements of the stars in the night sky can also serve to guide the traveller, and particularly the traveller at sea who has
no other landmarks. That is what astronomy meant to the navigators of the Mediterranean in the Old World. But so far as we can judge, the peoples of the New World did not use astronomy as a scientific guide for land and ocean voyages. And without astronomy it is really not possible to find your way over great distances, or even to have a theory about the shape of the earth and the land and sea
on it. Columbus was working with an old and, to our minds, crude astronomy when he set sail for the other side of the world: for instance, he thought that the earth was much smaller than it really is. Yet Columbus found the New World. It cannot be an accident that the New World never thought that the earth is round, and never went out to look for the Old World. It was the Old World which set sail
round the earth to discover the New.
Astronomy is not the apex of science or of invention. But it is a test of the cast of temperament and mind that underlies a culture. The seafarers of the Mediterranean since Greek times had a peculiar inquisitiveness that combined adventure with logic – the empirical with the rational – into a single mode of inquiry. The New World
did not.
Then did the New
World invent nothing? Of course not. Even so primitive a culture as Easter Island made one tremendous invention, the carving of huge and uniform statues. There is nothing like them in the world, and people ask, as usual, all kinds of marginal and faintly irrelevant questions about them. Why were they made like this? How were they transported? How did they get to the places that they are at? But
that is not the significant problem. Stonehenge, of a much earlier stone civilisation, was much more difficult to put up; so was Avebury, and many other monuments. No, primitive cultures do inch their way through these enormous communal enterprises.
The critical question about these statues is, Why were they all made
alike
? You see them sitting there, like Diogenes in their barrels, looking at
the sky with empty eye-sockets, and watching the sun and the stars go overhead without ever trying to understand them. When the Dutch discovered this island on Easter Sunday in 1722, they said that it had the makings of an earthly paradise. But it did not. An earthly paradise is not made by this empty repetition, like a caged animal going round and round, and making always the same thing. These
frozen faces, these frozen frames in a film that is running down, mark a civilisation which failed to take the first step on the ascent of rational knowledge. That is the failure of the New World cultures, dying in their own symbolic Ice Age.
Easter Island is over a thousand miles from the nearest inhabited island, which is Pitcairn Island, to the west. It is over fifteen hundred miles from the
next, the Juan Fernandez Islands to the east, where Alexander Selkirk, the original for Robinson Crusoe, was stranded in 1704. Distances like that cannot be navigated unless you have a model of the heavens and of star positions by which you can tell your way. People often ask about Easter Island, How did men come here? They came here by accident: that is not in question. The question is, Why could
they not get off? And they could not get off because they did not have a sense of the movement of the stars by which to find their way.
Why not? One obvious reason is that there is no Pole Star in the southern sky. We know that is important, because it plays a part in the migration of birds, which find their way by the Pole Star. That is perhaps why most bird migration is in the northern hemisphere
and not in the southern.
The absence of a Pole Star could be meaningful down here in the southern hemisphere, but it cannot be meaningful for the whole of the New World. Because there is Central America, there is Mexico, there are all sorts of places which also did not have an astronomy and yet which lie north of the equator.
What was wrong there? Nobody knows. I think that they lacked that
great dynamic image which so moved the Old World – the wheel. The wheel was only a toy in the New World. But in the Old World it was the greatest image of poetry and science; everything was founded on it. This sense of the heavens moving round their hub inspired Christopher Columbus when he set sail in 1492, and the hub was the round earth. He had it from the Greeks, who believed that the stars were
fixed on spheres which made music as they turned. Wheels within wheels. That was the system of Ptolemy that had worked for over a thousand years.
More than a hundred years before Christopher Columbus set sail, the Old World had been able to make a superb clockwork of the starry heavens. It was made by Giovanni de Dondi in Padua in about 1350. It took him sixteen
years, and it is sad that the
original has not survived. Happily, it has been possible to build a duplicate from his working drawings, and the Smithsonian Institution in Washington houses the marvellous model of classical astronomy that Giovanni de Dondi designed.
But more than the mechanical marvel is the intellectual conception, which comes from Aristotle and Ptolemy and the Greeks. De Dondi’s clock is their view of the
planets as seen from the earth. From the earth there are seven planets – or so the ancients thought, since they counted the sun also as a planet of the earth. So the clock has seven faces or dials, and on each face rides a planet. The path of the planet on its dial is (approximately) the path that we see from the earth – the clock is about as accurate as observation was when it was made. Where the
path looks circular from the earth, it is circular on its dial; that was easy. But where the path of a planet loops back on itself when seen from the earth, de Dondi has a mechanical combination of wheels which copies the epicycles (that is, the rolling of circles on circles) by which Ptolemy had described it.
First, then, the Sun: a circular path, as it seemed then. The next dial shows Mars:
its motion is running on a clockwork wheel inside a wheel. Then Jupiter: more complex wheels within wheels. Next Saturn: wheels within wheels. Then we come to the Moon – her dial is simple, because she truly is a planet of the earth, and her path is shown as circular. Lastly we come to the dials for the two planets that lie between us and the Sun; that is, to Mercury, and finally to Venus. And again
the same picture: the wheel that carries Venus turns inside a larger, hypothetical wheel.