The Clockwork Universe (17 page)

Chapter Twenty-Nine
Sputnik in Orbit, 1687

In a story called “The Red-Headed League,” Dr. Watson looks hard at Sherlock Holmes's latest visitor, but nothing strikes him as noteworthy. He turns toward the great detective. Perhaps
Holmes has seen more? “Beyond the obvious facts that he has at
some time done manual labour, that he takes snuff, that he is a
Freemason, that he has been in China, and that he has done a considerable amount of writing lately, I can deduce nothing
else,” says Holmes.

Galileo and his fellow scientists favored a similar technique. By paying close attention to what others had overlooked, they could find their way to utterly unexpected conclusions. Galileo's analysis of life on shipboard showed, for instance, that a marble that rolled off a table would take precisely the same time to reach the floor whether the ship was moving at a steady speed or standing still. The ship's horizontal motion has no effect on the rock's vertical fall. In Galileo's hands, that seemingly small observation had momentous consequences.

Picture any projectile moving through the air—a baseball
soaring toward the outfield, a penny flipped into the air, a dancer leaping across the stage. In all such cases, the moving
object's horizontal motion and its vertical motion take place
independently and can be examined separately. The horizontal
movement is steady and unchanging, in line with Galileo's law of motion. Ball and coin and dancer travel a certain distance hori
zontally in the first second, the same distance in the next second,
and so on, moving at a constant speed from liftoff until touch
down.
³⁸
At the same time, the projectile's
vertical
progress—
its height above the ground—changes according to a different rule. At the moment of launch, the projectile rises quickly but then it rises slower and slower, stops rising altogether, and sits poised for an instant neither rising nor falling, and then plummets earthward faster and faster. The change in speed follows a simple, precise rule, and the upward part of the flight and the downward part are exactly symmetrical.

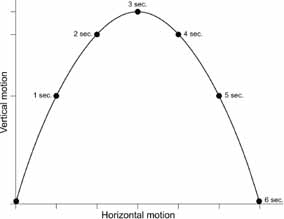
Any object launched into the air—arrow, bullet, cannonball—travels in a curved path like this one. The moving object covers the same
horizontal
distance during each second of its flight.

Mathematically, it's easy to show that the combination of steady horizontal motion and steadily changing vertical motion makes for a parabolic path. (A parabola is an arch-shaped curve, but it is not just a generic arch; it is one that satisfies specific technical conditions, just as an ellipse is not a generic oval but one of a specific sort.) Parabolas had been painted against the sky ever since the first caveman threw a rock, but no one before Galileo had ever recognized them, and he was immensely proud of his discovery. “It has been observed that missiles and projectiles describe a curved path of some sort,” he wrote. “However no one has pointed out the fact that this path is a parabola. But this and other facts, not few in number or less worth knowing, I have succeeded in proving.”

God had once again shown his taste for geometry. The planets in the heavens traveled not in haphazard curves but in perfect ellipses, and objects here on Earth traced exact parabolas.

Concealed within the same observation about the independence of horizontal motion and vertical motion was a further surprise. Galileo might have found it, but he didn't. Isaac Newton did. Imagine someone firing a gun horizontally, and at the same instant someone standing next to the shooter and dropping a bullet from the same height as the gun. When the two bullets reach the ground, they will be far apart. The one shot from the gun will have traveled hundreds of yards; the other will rest in the grass directly below the spot where it was dropped. Which bullet will hit the ground first?

Surprisingly, both reach the ground at exactly the same
moment. That's what it means for the bullet's vertical motion—
its fall—to be independent of its horizontal motion. For Newton,
that was enough to draw a remarkable conclusion.

Suppose it takes one second for a bullet dropped from a
cer
tain height to hit the ground. That means that a bullet shot
horizontally from the same height would also hit the ground in one second. A more powerful gun would send the bullet faster and farther, but—if the ground was perfectly flat—that bullet, too, would fall to the ground in one second.

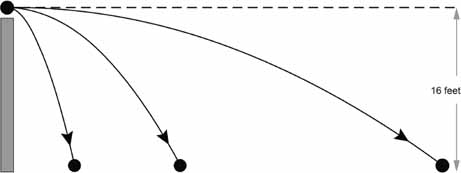
Bullets shot horizontally with different force travel different distances before they come to rest, but they all
fall
at the same rate. Each second a bullet is in the air it falls 16 feet toward the ground.

Newton preferred to imagine a cannon blasting away horizontally. He imagined faster and faster cannonballs, covering greater and greater distances in their one-second journey. But the Earth is round, not flat.

That makes all the difference. Since the Earth isn't flat, it curves away beneath the speeding cannonball. In the meantime, the cannonball is falling toward the ground. Suppose you fired a cannonball from high above the atmosphere, horizontally. With nothing to slow it down, it would continue at the same speed forever, falling all the while. If you launched it at just the right speed, then by the time the cannonball had fallen, say, four feet, the ground itself would have fallen four feet below horizontal.

And then what? The cannonball would continue on its journey forever, always falling but never coming any closer to the ground. Why? Because the cannonball always falls at the same rate, and the ground always curves beneath it at the same rate, so the cannonball falls and falls, and the Earth curves and curves, and the picture never changes. We've launched a satellite.

Newton pictured it all in 1687.

Chapter Thirty
Hidden in Plain Sight

Kepler had taken the first giant steps toward showing that
mathematics governed the heavens. Galileo showed that mathematics reigned here on Earth. Newton's great achievement, to peek ahead for a moment, was to demonstrate that Kepler's discoveries and Galileo's fit seamlessly together, and to explain why.

It was Kepler who spelled out explicitly the credo that all the great seventeenth-century scientists endorsed. When he began studying astronomy he had talked of planets as if they had souls. He soon recanted. The planets surely moved, but their motion had nothing in common with that of galloping horses or leaping porpoises. “My aim is to show that the machine of the universe is not similar to a divine animated being,” Kepler declared, “but similar to a clock.”

Galileo was the first to grasp, in detail, the workings of the cogs and gears of that cosmic clock. He liked to tell a story, perhaps invented, about how he had made his first great discovery. He had been young and bored, in church, daydreaming. An attendant had lit the candles on a giant chandelier and inadvertently set it swinging. Rather than listen to the service, Galileo watched the chandelier. It swung widely at first and then gradually in smaller and smaller arcs. Using his pulse beat to measure the time (in his day no one had yet built a clock with a second hand), Galileo discovered what has ever since been known as the law of pendulums—a pendulum takes the same time to swing through a small arc as through a large one.

Perhaps it was because Galileo had been raised in a musical
household—his father was a renowned composer and musician—
that counting time came naturally to him.
³⁹
Eventually his counting would lead to one of history's profound discoveries. What Galileo did, and what no one before him had ever done, was find a new way to think about time. It was an accomplishment akin to a fish's finding a new way to think about water. “Galileo spent twenty years wrestling with the problem before he got free of
man's natural biological instinct for time as that in which he lives
and grows old,” wrote the historian Charles C. Gillispie. “Time eluded science until Galileo.”

Galileo's solution was so successful and so radical that every
one today—even those without the slightest knowledge of physics—takes his insight for granted. The breakthrough was to identify time—not distance or temperature or color or any
of a thousand other possibilities—as the essential variable that governs the world. For years Galileo had tried to find a relationship between the speed of a falling object and the distance it had
fallen. All his efforts failed. Finally he turned away from dis
tance and focused on time. Suddenly everything fell into place. Galileo had found a way to pin numbers to the world.

The crucial experiments might have occurred only to a musician. Once again they involved rolling a ball down a ramp. The setup was bare-bones: a wooden ramp with a thin groove down the middle, a bronze ball to roll down the groove, and a series of movable catgut strings. The strings lay on the surface of the ramp, at a right angle to the groove, like frets on the neck of a guitar. When the ball crossed a string, it made an audible click but its speed continued almost unchanged.

Galileo may actually have dropped rocks from the Leaning Tower of Pisa, as legend has it, but if he did they fell too quickly
to study. So he picked up a ball, released it at the top of the
ramp, and cocked his ears.

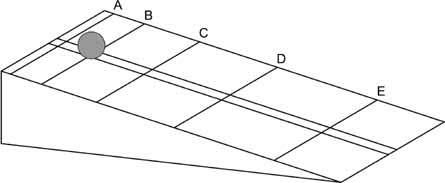
Now the strings came into play. Galileo could hear the ball cross each string in turn, and he painstakingly rolled the ball again and again, each time trying to position the strings so that the travel time between each pair of strings was the same. He needed to arrange the strings, in other words, so that the time it took the ball to move from the top of the ramp to string A was the same as the time it took to move from string A to string B, which was the same as the time from B to C, and C to D, and so on. (He measured time intervals by weighing the water that leaked through a hole in the bottom of a jug. Twice as much water meant twice as much time.) It was finicky, tedious work.

Finally satisfied, Galileo measured the distance between
strings. That yielded this little table.

The pattern in the right-hand column was easy to spot, but Galileo looked at the numbers again and recast the same data into a new table. Instead of looking at the ball as it traveled from one string to the next, he focused on the total distance the ball had traveled from the starting line. (All he had to do was add up the distances in the right-hand column.) This time he saw something more tantalizing.

Each number in the right column of this new table represented the distance the ball had traveled in a certain amount of time—in one second, in two seconds, in three seconds, and so on. That distance, Galileo saw, could be expressed as a function
of time. In
t
seconds, a ball rolling down a ramp at gravity's
command traveled precisely
t
²
inches.
⁴⁰
In 1 second, a ball rolled
1
²
inches, in 2 seconds 2
²
inches, in 5 seconds 5
²
inches, and
so on.

What was just as surprising was what the law
didn't
say—it didn't say anything about how much the ball weighed. Roll a cannonball and a BB down a ramp in side-by-side grooves, and they would travel alongside one another all the way and reach the bottom at precisely the same moment. For a given ramp, the same tidy law always held—the distance the ball traveled was proportional to time squared. All that counted was the height above the ground of the point where the ball was released.

Repeat the experiment on a steeper ramp, and the cannonball and the BB would both travel faster, but they would still travel side by side every inch of the way. That was enough. Galileo made a daring leap: what held for a steep ramp and for an even steeper ramp would also hold for the steepest “ramp” of all, a free fall through the air. All objects, regardless of their weight, fall at exactly the same rate.