The Code Book (30 page)

As the weeks passed, Turing realized that Bletchley was accumulating a vast library of decrypted messages, and he noticed that many of them conformed to a rigid structure. By studying old decrypted messages, he believed he could sometimes predict part of the contents of an undeciphered message, based on when it was sent and its source. For example, experience showed that the Germans sent a regular enciphered weather report shortly after 6
A.M
. each day. So, an encrypted message intercepted at 6:05
A.M
. would be almost certain to contain wetter, the German word for “weather.” The rigorous protocol used by any military organization meant that such messages were highly regimented in style, so Turing could even be confident about the location of wetter within the encrypted message. For example, experience might tell him that the first six letters of a particular ciphertext corresponded to the plaintext letters wetter. When a piece of plaintext can be associated with a piece of ciphertext, this combination is known as a
crib
.
Turing was sure that he could exploit the cribs to crack Enigma. If he had a ciphertext and he knew that a specific section of it, say ETJWPX, represented wetter, then the challenge was to identify the settings of the Enigma machine that would transform wetter into ETJWPX. The straightforward, but impractical, way to do this would be for the cryptanalyst to take an Enigma machine, type in wetter and see if the correct ciphertext emerged. If not, then the cryptanalyst would change the settings of the machine, by swapping plugboard cables, and swapping or reorienting scramblers, and then type in wetter again. If the correct ciphertext did not emerge, the cryptanalyst would change the settings again, and again, and again, until he found the right one. The only problem with this trial and error approach was the fact that there were 159,000,000,000,000,000,000 possible settings to check, so finding the one that transformed wetter into ETJWPX was a seemingly impossible task.
To simplify the problem, Turing attempted to follow Rejewski’s strategy of disentangling the settings. He wanted to divorce the problem of finding the scrambler settings (finding which scrambler is in which slot, and what their respective orientations are) from the problem of finding the plugboard cablings. For example, if he could find something in the crib that had nothing to do with the plugboard cablings, then he could feasibly check each of the remaining 1,054,560 possible scrambler combinations (60 arrangements × 17,576 orientations). Having found the correct scrambler settings, he could then deduce the plugboard cablings.
Eventually, his mind settled on a particular type of crib which contained internal loops, similar to the chains exploited by Rejewski. Rejewski’s chains linked letters within the repeated message key. However, Turing’s loops had nothing to do with the message key, as he was working on the assumption that soon the Germans would stop sending repeated message keys. Instead, Turing’s loops connected plaintext and ciphertext letters within a crib. For example, the crib shown in
Figure 48
contains a loop.

Figure 48
One of Turing’s cribs, showing a loop.
Remember, cribs are only guesses, but if we assume that this crib is correct, we can link the letters W→E, e→T, t→W as part of a loop. Although we know none of the Enigma machine settings, we can label the first setting, whatever it is, S. In this first setting we know that w is encrypted as E. After this encryption, the first scrambler clicks around one place to setting S+1, and the letter e is enciphered as T. The scrambler clicks forward another place and encrypts a letter that is not part of the loop, so we ignore this encryption. The scrambler clicks forward one more place and, once again, we reach a letter that is part of the loop. In setting S+3, we know that the letter t is enciphered as W. In summary, we know that
In setting S, Enigma encrypts w as E.
In setting S+1, Enigma encrypts e as T.
In setting S+3, Enigma encrypts t as W.
So far the loop seems like nothing more than a curious pattern, but Turing rigorously followed the implications of the relationships within the loop, and saw that they provided him with the drastic shortcut he needed in order to break Enigma. Instead of working with just one Enigma machine to test every setting, Turing began to imagine three separate machines, each dealing with the encipherment of one element of the loop. The first machine would try to encipher w into E, the second would try to encipher e into T, and the third t into W. The three machines would all have identical settings, except that the second would have its scrambler orientations moved forward one place with respect to the first, a setting labeled S+1, and the third would have its scrambler orientations moved forward three places with respect to the first, a setting labeled S+3. Turing then pictured a frenzied cryptanalyst, continually changing plugboard cables, swapping scrambler arrangements and changing their orientations in order to achieve the correct encryptions. Whatever cables were changed in the first machine would also be changed in the other two. Whatever scrambler arrangements were changed in the first machine would also be changed in the other two. And, crucially, whatever scrambler orientation was set in the first machine, the second would have the same orientation but stepped forward one place, and the third would have the same orientation but stepped forward three places.
Turing does not seem to have achieved much. The cryptanalyst still has to check all 159,000,000,000,000,000,000 possible settings, and, to make matters worse, he now has to do it simultaneously on all three machines instead of just one. However, the next stage of Turing’s idea transforms the challenge, and vastly simplifies it. He imagined connecting the three machines by running electrical wires between the inputs and the outputs of each machine, as shown in
Figure 49
. In effect, the loop in the crib is paralleled by the loop of the electrical circuit. Turing pictured the machines changing their plugboard and scrambler settings, as described above, but only when all the settings are correct for all three machines would the circuit be completed, allowing a current to flow through all three machines. If Turing incorporated a lightbulb within the circuit, then the current would illuminate it, signaling that the correct settings had been found. At this point, the three machines still have to check up to 159,000,000,000,000,000,000 possible settings in order to illuminate the bulb. However, everything done so far has merely been preparation for Turing’s final logical leap, which would make the task over a hundred million million times easier in one fell swoop.
Turing had constructed his electrical circuit in such a way as to nullify the effect of the plugboard, thereby allowing him to ignore the billions of plugboard settings.
Figure 49
shows that the first Enigma has the electric current entering the scramblers and emerging at some unknown letter, which we shall call L
1
. The current then flows through the plugboard, which transforms L
1
into E. This letter E is connected via a wire to the letter e in the second Enigma, and as the current flows through the second plugboard it is transformed back to L
1
. In other words, the two plugboards cancel each other out. Similarly, the current emerging from the scramblers in the second Enigma enters the plugboard at L
2
before being transformed into T. This letter T is connected via a wire to the letter t in the third Enigma, and as the current flows through the third plugboard it is transformed back to L
2
. In short, the plugboards cancel themselves out throughout the whole circuit, so Turing could ignore them completely.
Turing needed only to connect the output of the first set of scramblers, L
1
, directly to the input of the second set of scramblers, also L
1
, and so on. Unfortunately, he did not know the value of the letter L
1
, so he had to connect all 26 outputs of the first set of scramblers to all 26 corresponding inputs in the second set of scramblers, and so on. In effect, there were now 26 electrical loops, and each one would have a lightbulb to signal the completion of an electrical circuit. The three sets of scramblers could then simply check each of the 17,576 orientations, with the second set of scramblers always one step ahead of the first set, and the third set of scramblers two steps ahead of the second set. Eventually, when the correct scrambler orientations had been found, one of the circuits would be completed and the bulb would be illuminated. If the scramblers changed orientation every second, it would take just five hours to check all the orientations.
Only two problems remained. First, it could be that the three machines are running with the wrong scrambler arrangement, because the Enigma machine operates with any three of the five available scramblers, placed in any order, giving sixty possible arrangements. Hence, if all 17,576 orientations have been checked, and the lamp has not been illuminated, it is then necessary to try another of the sixty scrambler arrangements, and to keep on trying other arrangements until the circuit is completed. Alternatively, the cryptanalyst could have sixty sets of three Enigmas running in parallel.
The second problem involved finding the plugboard cablings, once the scrambler arrangement and orientations had been established. This is relatively simple. Using an Enigma machine with the correct scrambler arrangement and orientations, the cryptanalyst types in the ciphertext and looks at the emerging plaintext. If the result is tewwer rather than wetter, then it is clear that plugboard cables should be inserted so as to swap w and t. Typing in other bits of ciphertext would reveal other plugboard cablings.
The combination of crib, loops and electrically connected machines resulted in a remarkable piece of cryptanalysis, and only Turing, with his unique background in mathematical machines, could ever have come up with it. His musings on the imaginary Turing machines were intended to answer esoteric questions about mathematical undecidability, but this purely academic research had put him in the right frame of mind for designing a practical machine capable of solving very real problems.
Bletchley was able to find £100,000 to turn Turing’s idea into working devices, which were dubbed bombes because their mechanical approach bore a passing resemblance to Rejewski’s bombe. Each of Turing’s bombes was to consist of twelve sets of electrically linked Enigma scramblers, and would thus be able to cope with much longer loops of letters. The complete unit would be about two meters tall, two meters long and a meter wide. Turing finalized the design at the beginning of 1940, and the job of construction was given to the British Tabulating Machinery factory at Letchworth.
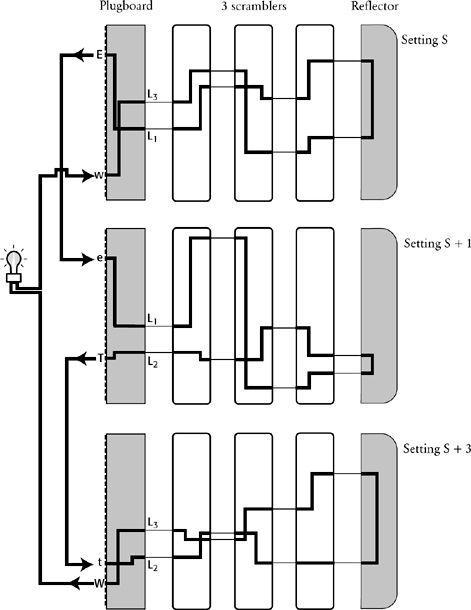
Figure 49
The loop in the crib can be paralleled by an electrical loop. Three Enigma machines are set up in identical ways, except that the second one has its first scrambler moved forward one place (setting S + 1), and the third has its scrambler moved forward two further places (setting S + 3). The output of each Enigma is then connected to the input of the next one. The three sets of scramblers then click around in unison until the circuit is complete and the light illuminates. At this point the correct setting has been found. In the diagram above, the circuit is complete, corresponding to the correct setting.
While waiting for the bombes to be delivered, Turing continued his day-to-day work at Bletchley. News of his breakthrough soon spread among the other senior cryptanalysts, who recognized that he was a singularly gifted codebreaker. According to Peter Hilton, a fellow Bletchley codebreaker, “Alan Turing was obviously a genius, but he was an approachable, friendly genius. He was always willing to take time and trouble to explain his ideas; but he was no narrow specialist, so that his versatile thought ranged over a vast area of the exact sciences.”
However, everything at the Government Code and Cypher School was top secret, so nobody outside of Bletchley Park was aware of Turing’s remarkable achievement. For example, his parents had absolutely no idea that Alan was even a codebreaker, let alone Britain’s foremost cryptanalyst. He had once told his mother that he was involved in some form of military research, but he did not elaborate. She was merely disappointed that this had not resulted in a more respectable haircut for her scruffy son. Although Bletchley was run by the military, they had conceded that they would have to tolerate the scruffiness and eccentricities of these “professor types.” Turing rarely bothered to shave, his nails were stuffed with dirt, and his clothes were a mass of creases. Whether the military would also have tolerated his homosexuality remains unknown. Jack Good, a veteran of Bletchley, commented: “Fortunately the authorities did not know that Turing was a homosexual. Otherwise we might have lost the war.”