The Singularity Is Near: When Humans Transcend Biology (13 page)
Read The Singularity Is Near: When Humans Transcend Biology Online
Authors: Ray Kurzweil
Tags: #Non-Fiction, #Fringe Science, #Retail, #Technology, #Amazon.com

Despite this massive deflation in the cost of information technologies, demand has more than kept up. The number of bits shipped has doubled every 1.1 years, faster than the halving time in cost per bit, which is 1.5 years.
30
As a result, the semiconductor industry enjoyed 18 percent annual growth in total revenue from 1958 to 2002.
31
The entire information-technology (IT) industry has grown from 4.2 percent of the gross domestic product in 1977 to 8.2 percent in 1998.
32
IT has become increasingly influential in all economic sectors. The share of value contributed by information technology for most categories of products and services is rapidly increasing. Even common manufactured products such as tables and chairs have an information content, represented by their computerized designs and the programming of the inventory-procurement systems and automated-fabrication systems used in their assembly.
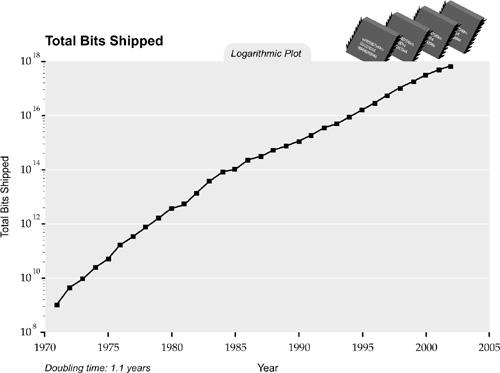
Doubling (or Halving) Times
33

Moore’s Law: Self-Fulfilling Prophecy?
Some observers have stated that Moore’s Law is nothing more than a self-fulfilling prophecy: that industry participants anticipate where they need to be at particular times in the future, and organize their research and development accordingly. The industry’s own written road map is a good example of this.
34
However, the exponential trends in information technology are far broader than those covered by Moore’s Law. We see the same types of trends in essentially every technology or measurement that deals with information. This includes many technologies in which a perception of accelerating price-performance does not exist or has not previously been articulated (see below). Even within computing itself, the growth in capability per unit cost is much broader than what Moore’s Law alone would predict.
The Fifth Paradigm
35
Moore’s Law is actually not the first paradigm in computational systems. You can see this if you plot the price-performance—measured by instructions per second per thousand constant dollars—of forty-nine famous computational systems and computers spanning the twentieth century (see the figure below).
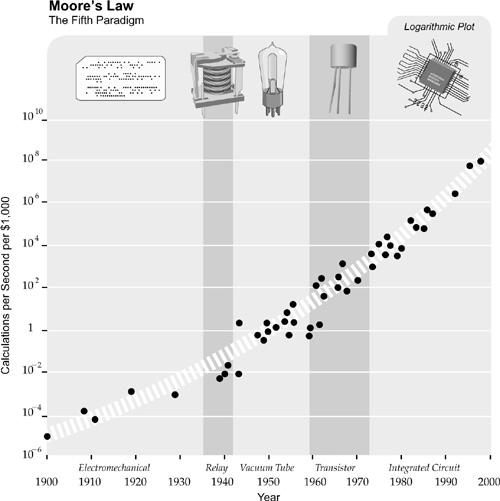
The five paradigms of exponential growth of computing:
Each time one paradigm has run out of steam, another has picked up the pace
.
As the figure demonstrates, there were actually four different paradigms—electromechanical, relays, vacuum tubes, and discrete transistors—that showed exponential growth in the price-performance of computing long before integrated circuits were even invented. And Moore’s paradigm won’t be the last. When Moore’s Law reaches the end of its S-curve, now expected before 2020, the exponential growth will continue with three-dimensional molecular computing, which will constitute the sixth paradigm.
Fractal Dimensions and the Brain
Note that the use of the third dimension in computing systems is not an either-or choice but a continuum between two and three dimensions. In terms of biological intelligence, the human cortex is actually rather flat, with only six thin layers that are elaborately folded, an architecture that greatly increases the surface area. This folding is one way to use the third dimension. In “fractal” systems (systems in which a drawing replacement or folding rule is iteratively applied), structures that are elaborately folded are considered to constitute a partial dimension. From that perspective, the convoluted surface of the human cortex represents a number of dimensions in between two and three. Other brain structures, such as the cerebellum, are three-dimensional but comprise a repeating structure that is essentially two-dimensional. It is likely that our future computational systems will also combine systems that are highly folded two-dimensional systems with fully three-dimensional structures.
Notice that the figure shows an exponential curve on a logarithmic scale, indicating two levels of exponential growth.
36
In other words, there is a gentle but unmistakable exponential growth in the
rate
of exponential growth. (A straight line on a logarithmic scale shows simple exponential growth; an upwardly curving line shows higher-than-simple exponential growth.) As you can see, it took three years to double the price-performance of computing at the beginning of the twentieth century and two years in the middle, and it takes about one year currently.
37
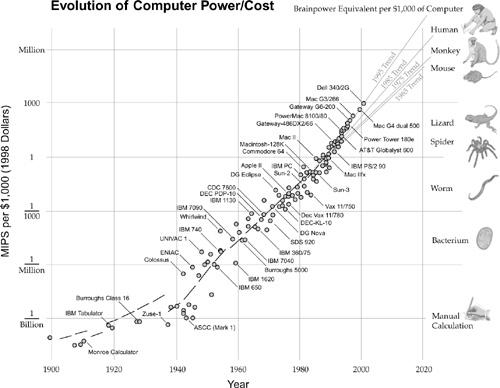
Hans Moravec provides the following similar chart (see the figure below), which uses a different but overlapping set of historical computers and plots trend lines (slopes) at different points in time. As with the figure above, the slope increases with time, reflecting the second level of exponential growth.
38
If we project these computational performance trends through this next century, we can see in the figure below that supercomputers will match human brain capability by the end of this decade and personal computing will achieve it by around 2020—or possibly sooner, depending on how conservative an estimate of human brain capacity we use. (We’ll discuss estimates of human brain computational speed in the next chapter.)
39
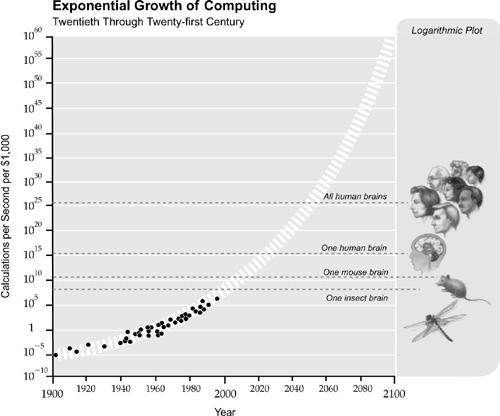
The exponential growth of computing is a marvelous quantitative example of the exponentially growing returns from an evolutionary process. We can express the exponential growth of computing in terms of its accelerating pace: it took ninety years to achieve the first MIPS per thousand dollars; now we add one MIPS per thousand dollars every five hours.
40

IBM’s Blue Gene/P supercomputer is planned to have one million gigaflops (billions of floating-point operations per second), or 10
15
calculations per second when it launches in 2007.
41
That’s one tenth of the 10
16
calculations per second needed to emulate the human brain (see the next chapter). And if we extrapolate this exponential curve, we get 10
16
calculations per second early in the next decade.
As discussed above, Moore’s Law narrowly refers to the number of transistors on an integrated circuit of fixed size and sometimes has been expressed even more narrowly in terms of transistor feature size. But the most appropriate measure to track price-performance is computational speed per unit cost, an index that takes into account many levels of “cleverness” (innovation, which is to say, technological evolution). In addition to all of the invention involved in integrated circuits, there are multiple layers of improvement in computer design (for example, pipelining, parallel processing, instruction look-ahead, instruction and memory caching, and many others).
The human brain uses a very inefficient electrochemical, digital-controlled analog computational process. The bulk of its calculations are carried out in the interneuronal connections at a speed of only about two hundred calculations per second (in each connection), which is at least one million times slower than contemporary electronic circuits. But the brain gains its prodigious
powers from its extremely parallel organization
in three dimensions
. There are many technologies in the wings that will build circuitry in three dimensions, which I discuss in the next chapter.
We might ask whether there are inherent limits to the capacity of matter and energy to support computational processes. This is an important issue, but as we will see in the next chapter, we won’t approach those limits until late in this century. It is important to distinguish between the S-curve that is characteristic of any specific technological paradigm and the continuing exponential growth that is characteristic of the ongoing evolutionary process within a broad area of technology, such as computation. Specific paradigms, such as Moore’s Law, do ultimately reach levels at which exponential growth is no longer feasible. But the growth of computation supersedes any of its underlying paradigms and is for present purposes an ongoing exponential.