Understanding Computation (43 page)

The
a
and
b
rules halve the input;
ccdddd
represents the number 2.

The
c
rule deletes the
leading
cc
pair and appends the
characters
eo
, one of which will
form the final result.

The empty
d
rule consumes all
of the leading
dd
pairs, leaving
only
eo
.

The
e
rule replaces
eo
with just
e
, and the system halts.

The number is halved as before, but because it’s an odd number this time, the result
is a string with an odd number of
d
s. Our encoding
scheme for numbers uses only pairs of characters, so
ccddddd
doesn’t strictly represent anything, but because it contains “two and
a half” pairs of
d
characters, it’s reasonable to think
of it informally as the number 2.5.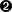

All the leading
dd
pairs get
deleted, leaving a solitary
d
before the final
eo
.

The leftover
d
is deleted and
takes the
e
with it, leaving just
o
, and the system halts.

Having a deletion number greater than 1 is essential for making this tag system work.
Because every
second
character triggers a rule, we can influence the
system’s behavior by arranging for certain characters to appear (or not appear) in these
trigger positions. This technique of making characters appear in or out of sync with the
deletion behavior is the key to designing a powerful tag system.

1. As the simplest possible example, take a Turing machine whose
   tape only uses two characters—we’ll call them
   0
and
   1
,
   with
   0
acting as the blank
   character.
   

2. Split the Turing machine’s tape into two pieces: the left part,
   consisting of the character underneath the tape head itself and all
   characters to its left, and the right part, consisting of all
   characters to the right of the head.
   

3. Treat the left part of the tape as a binary number: if the
   initial tape looks like
   0001101(0)0011000
, the left part is the
   binary number 11010, which is 26 in decimal.
   

4. Treat the right part of the tape as a binary number
   written
   backward
   : the right part of our example tape is the binary number 1100, or 12
   in decimal.
   

5. Encode those two numbers as a string suitable for use by a tag system. For our example
   tape, we could use
   aa
followed by 26 copies of
   bb
, then
   cc
followed by 12
   copies of
   dd
.
   

6. Use simple numerical operations—doubling, halving, incrementing,
   decrementing, and odd/even checking—to simulate reading from the tape,
   writing to the tape, and moving the tape head. For instance, we can
   move the head right on our example tape by doubling the number
   representing the left part and halving the number representing the
   right part:
   ^{[
   59
   ]}
   doubling 26 gives 52, which is 110100 in binary; half of
   12 is 6, which is 110 in binary; so the new tape looks like
   011010(0)011000
. Reading from the tape means
   checking whether the number representing the left part of the tape is
   even or odd, and writing a
   1
or
   0
to the tape means incrementing or
   decrementing that number.
   

7. Represent the current state of the simulated Turing machine with the choice of
   characters used to encode the left and right tape numbers: perhaps when the machine is in
   state 1, we encode the tape with
   a
,
   b
,
   c
, and
   d
characters, but when it moves into state 2, we use
   e
,
   f
,
   g
, and
   h
instead, and so
   on.
   

8. Turn each Turing machine rule into a tag system that rewrites
   the current string in the appropriate way. A rule that reads a
   0
, writes a
   1
, moves the tape head right and goes into
   state 2 could become a tag system that checks that the left tape
   number is even, increments it, doubles the left tape number while
   halving the right tape number, and produces a final string that is
   encoded with state 2’s characters.
   

9. Combine these individual tag systems to make one large system
   that simulates every rule of the
   Turing machine.